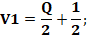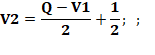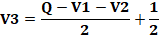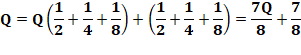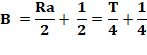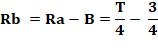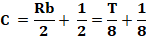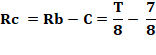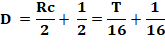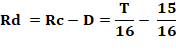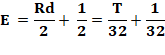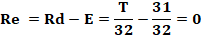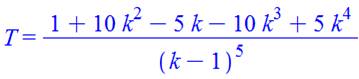|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PARTAGES IMPOSSIBLES ? Au départ, cela semble impossible. Avec un petit truc ça marche. Mais lequel? |
|
|
|||||||||||||||||
|
Énigme
Puis la moitié et ½. Et encore la moitié et ½. J'ai tout vendu sans casser d'œuf. Solution
Solution en équations Q = V1 + V2 + V3
Somme des trois ventes
Q = 7 Généralisation 1 –
Mêmes proportions
Généralisation 2
- Proportions rationnelles
Exemple : pour p = 3, q = 4 et n = 5
Cité en Excursions in Number Theory"
(C.S. Ogilvy & J.T.Anderson) Merci
à Jos Heynderickx pour cette référence Une idée de la justification Pour n = 5 et en prenant q = p – 1, on calcule
la somme. On trouve:
Avec une identité
remarquable
Solution T = q5. La généralisation pour n quelconque se lit
sur la formule. Reste une question: existe-t-il d'autres
solutions que q = p – 1? Non! La configuration sympathique qui a permis
l'application de l'identité remarque ne se reproduit pas. La formule générale pour p et q quelconques
et n = 5 est:
|
|||||||||||||||||
Voir Énigme des
œufs qui tombent du centième étage
Incroyable!
|
Un
œuf non fécondé ne fait qu'une seule cellule
géante! Du moins c'est le cas du jaune d'œuf. Le blanc, la membrane et la
coquille sont des enveloppes supplémentaires. |
|
|
||||||||||||||||||||||||||||||||||||
|
Énigme
En rentrant, j'en donne la moitié plus un
demi à Isabelle, puis la moitié de ceux qui me restent plus
un demi à Christelle et le dernier que j'ai dans les mains à
Guillaume. Combien y avait-il de livres? Solution Il y avait 7 livres.
(il restait 1: la moitié de 1 plus 1/2
donne bien 1)
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
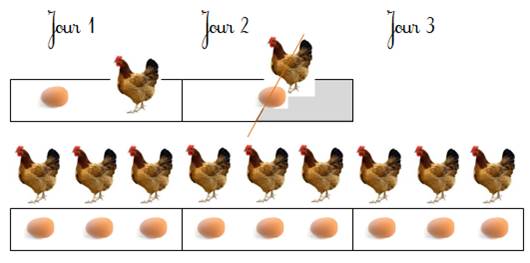
Énigme Le fermier facétieux constate qu'en moyenne:
une poule et demie pond un œuf et demi en un jour et demi. Il demande plein de
malices: combien pondent trois poules en trois jours? Solution C'est qu'une poule pond 1 œuf par jour (Voir illustration). Donc: 3 poules en pondent 3 par jour. Réponse pour 3 jours et 3 poules: 9 œufs. Illustration
|
|
|
|
|
|
Énigme
Aîné: 1/2; Puîné: 1/3; Benjamin: 1/9. Mais c'est impossible. La moitié de 17
c'est 8,5. On ne va tout de même pas découper les chevaux … Erreur du père ? Non, il y a une solution! Formulation narrative à la manière d'un conte Un
vieil homme, sentant sa mort prochaine, fit venir ses trois enfants pour leur
léguer ses chevaux. Il laissa à l'aîné la moitié de ses chevaux. Il laissa au
cadet le tiers de ses chevaux. Il laissa au benjamin un neuvième de ses
chevaux. A la mort du vieil homme les enfants s'aperçurent qu'il y avait
dix-sept chevaux. Ne voulant ni vendre ni tuer aucune des bêtes, et ils ne
trouvaient pas de moyen de faire le partage tel que voulu par leur père. Alors,
ils en parlent au fermier voisin, un homme pragmatique, dans l'espoir qu'il
puisse trouver une solution à leur problème. Le fermier prit connaissance du
testament, et les yeux pétillants, il alla chercher son propre cheval et
l'ajouta aux autres. Ce qui faisait dix-huit chevaux. Dès
lors, il devint tout à fait possible aux héritiers de procéder au partage,
tel que l'avait prévu le testament de leur père et, bien entendu, le fermier
récupéra son propre cheval. Solution
Explication
Généralisation
|
|
Voir Fractions unitaires / Nombre 17
|
|
|||||||||||||||||
|
Énigme Un promoteur vend les cinq villas du lotissement.
Les prix sont variés selon la superficie et la taille des villas
Quel est le total de la vente? Solution
Généralisation Si nous prenons 1/k au lieu de ½, la
solution est:
Exemples: k = 3/2, alors T = 242; k 5/4; alors T = 3 124; etc. T est un nombre entier pour k = (p + 1) / p
et alors:
|
|||||||||||||||||
|
|
|
|
Énigme >>> |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Énigme Un commerçant vend ses poissons: Il vend la moitié de ce qu'il possède plus
un demi-poisson. Puis, le tiers de ce qui reste plus un
tiers. Encore le quart des poissons plus un quart
de poisson. Et un cinquième des poissons et un
cinquième de poisson. Il lui reste 11 poissons. Quelle est la quantité de départ? Solution
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||
|
Énigme Combien y a-t-il d'œufs dans le panier, en
les disposant comme suit:
Solution N
= 2a + 1 = 3b + 2 = 4c + 3 = 5d + 4 = 2 x 29 + 1
= 3 x 19 + 2 = 4 x 14 + 3 = 5 x 11 + 4 = 59 Équation –
résolution en fonction de d
Quelques
solutions N a b c
d 59
14 19 29 11 119 29 39
59 23 179 44 59
89 35 239 59 79
119 47 60k-1
15k-1 20k-1 30k-1
12k-1 |
|||||||||||
Voir Modulo
/ Énigme du défilé
|
|
|||||||||||||||
|
Énigme Trois amis A, B et C décident de
faire un repas en commun. Solution
|
|||||||||||||||
|
|
|
|
Énigme >>> |
|
|
|
|
|
Énigme Cinq hommes et un singe font une provision
de noix de coco. Durant la nuit le premier se lève et prend
sa part (1/5); il en reste une qu'il donne au singe. Le deuxième se lève un peu plus tard et fait
la même chose: il prend 1/5 de qui reste et en donne une au singe. Même chose jusqu'au cinquième. La troupe se lève au petit matin et décide
de faire le partage. Chacun reçoit sa part et il ne reste pas de
noix de coco. Combien de noix de coco au départ? |
|
![]()
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
![]()