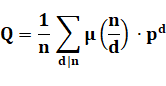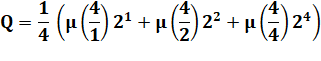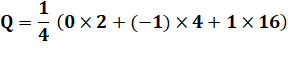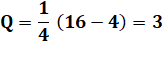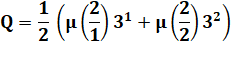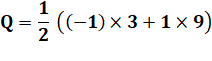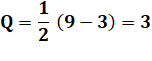Polynômes irréductibles

Édition du: 13/11/2022

INDEX Polynômes Arithmétique et algèbre	POLYNÔMES
	Introduction	Propriétés	Division	Divisibilité
	Unitaire	Exercices	Ex. de divisions
	Polynômes irréductibles

Faites un double-clic pour un retour en haut de page

Polynômes irréductibles sur F_p

Corps finis

Où il est question de factorisation des polynômes comme on réalise la factorisation des nombres entiers. Comme il existe des nombres premiers, il existe des polynômes "premiers" dits polynômes irréductibles.

Les applications sont nombreuses notamment en cryptologie. On s'intéresse alors à certains polynômes définis dans un certain cadre dit corps de Galois ou corps finis.

Comme avec les congruences, on transforme le monde infini des nombres en un monde fini, avec ces mêmes congruences on crée un monde fini de polynômes.

Sommaire de cette page

>>> Approche

>>> Polynômes dans F₂

>>> Polynômes irréductibles dans F₂

>>> Exercice

>>> Formule de Gauss

>>> Irréductibles sur F₃

Débutants

Technique de base

de l'algèbre

Glossaire

Polynômes

Anglais: irreductible polynomial: a polynomial that cannot be factored into the product of two non-constant polynomials.

Approche – Factorisations			haut
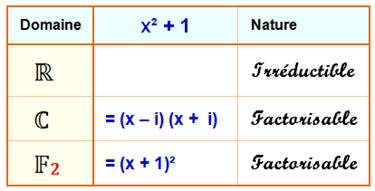
La factorisation du polynôme x² + 1 n'est pas réalisable dans le domaine des nombres réels car il n'existe pas de nombres réels tels que (x – a) (x – b) = x² + 1. Elle est possible dans le domaine des complexes et les racines sont +i et –i . C'est d'ailleurs un des intérêts des nombres complexes. Dans le domaine F_{2 ,}on a cette égalité inattendue: x² + 1 = (x + 1)². Dans ce domaine F₂, où on compte en binaire, on a, en effet: 2 = 0.		Exemple
D'une manière générale	Les polynômes du premier degré sont toujours irréductibles. Dans ℂ seuls les polynômes du premier degré sont irréductibles Dans ℝ , les polynômes irréductibles sont les polynômes du premier degré et les polynômes du deuxième degré de discriminant strictement négatif.

Domaine F₂

À ce niveau d'explications, sachons seulement que ce domaine F₂ concerne les polynômes dont les coefficients sont 0 ou 1, seulement (des polynômes dont les coefficients sont calculés en mod 2).

En présence d'opérations sur ces coefficients, on les traitera comme en binaire sur un seul bit. Ainsi: 1 + 1 = 0.

La définition de ces domaines en F₂, F₃, F_p (avec p premier) viendra plus loin.

Polynômes dans F₂ ou GF[2]		haut
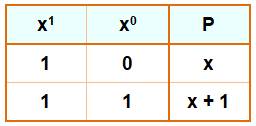
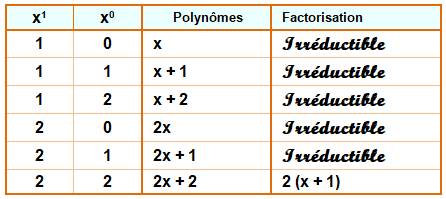
Premier degré Avec des coefficients 0 ou 1, le coefficient de x étant nécessairement 1 (premier degré), on a deux polynômes du premier degré dans F₂ : x et x + 1
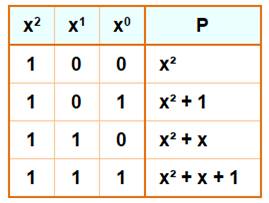
Deuxième degré Avec le même principe, le tableau montre l'existence de quatre polynômes du deuxième degré dans F₂ : x², x² + 1, x² + x et x² + x + 1
Troisième degré Dans ce cas, ils sont huit (8 = 2³). Il y en aura seize pour le quatrième degré (16 = 2⁴). Etc.

Factorisation dans F₂

haut

Méthode

L'idée consiste à lister les polynômes un par un et à éliminer tous ceux qui sont des produits de polynômes.

Prenons l'exemple paradoxal de

x² + 1 = (x + 1)² dans F₂.

Les racines possibles sont 0 ou 1. On teste simplement si la fonction prend la valeur 0 pour une de ces valeurs.

Si oui, cette valeur est une racine.

Si la racine est nulle, la factorisation est évidente.

Sinon le polynôme facteur est (x + 1). L'autre polynôme résulte de la division.

Recherche de racines

Avec x = 0 => x² + 1 = 0 + 1 = 1 => ce n'est pas une racine.

Avec x = 1 => x² + 1 = 1 + 1 = 2 = 0 => c'est une racine.

Factorisation

On divise x² + 1 par x + 1 et on trouve x + 1.

En effet: (x + 1)² = x² + 2x + 1 = x² + 0x + 1 = x² + 1

Car dans F₂ (monde binaire): 1 + 1 = 2 = 0.

(on dit aussi: 2 mod 2 = 0)

Division posée

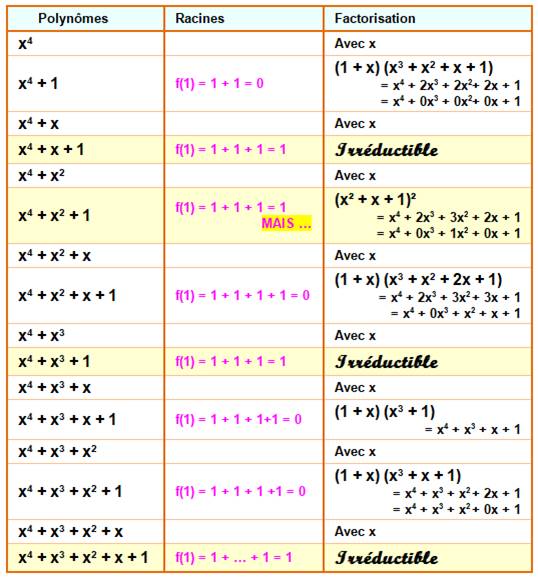
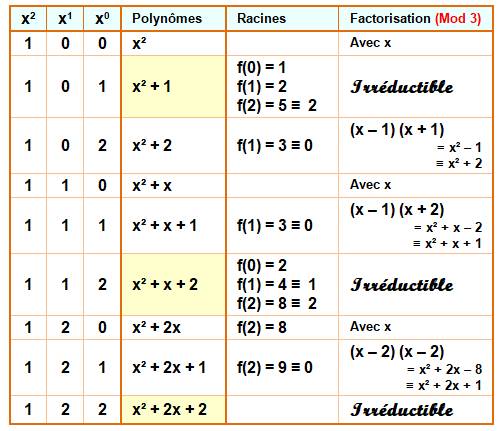
Polynômes irréductibles sur F₂		haut
Degré 1, 2 et 3 Le tableau montre, en colonne 1, la liste de tous les polynômes du premier, deuxième et troisième degré dans F₂. La colonne 2 indique les possibilités de racines (oui, si f(x) = 0). La colonne 3 donne la factorisation lorsqu'elle est possible. Trouver la factorisation par x est assez immédiate. Dans le cas où ni f(0) ni f(1) n'est nul, alors le polynôme est irréductible. Il y a un seul polynôme irréductible pour le deuxième degré et deux pour le troisième.
Degré 4 Le tableau montre les trois polynômes irréductibles dans F₂. Les treize autres sont réductibles ou factorisables. Avec le quatrième degré, il est possible que les deux facteurs soient du deuxième degré. Le test avec f(1) ne suffit plus. C'est le cas pour x⁴ + x² + 1.

Exercice

haut

Problème

Montrer que ce polynôme est irréductible dans F₂.

avec

Calculs préliminaires utiles

Solution

S'agissant d'un polynôme du troisième degré, les polynômes facteurs seront du premier et du deuxième degré.

Avec un facteur du premier degré, il suffit de montrer que f(x) n'est pas nul pour chacune des valeurs possibles.

Ce qui est le cas. La fonction f(x) est irréductible dans F₂.

Corps finis

Le domaine en F₂, généralisé en F_p (avec p premier) est un corps fini ou corps de Galois (finite field or Galois field) , noté aussi GF(p).

L'ensemble GF(p) comprend tous les polynômes dont les coefficients sont calculés mod p.

Dans GF(2) le polynôme x² + x + 1 est irréductible, alors que x² + 1 l'est.
En effet: (x + 1) (x + 1) = x² + 2x + 1 ≡ x² + 1 mod 2.

Le nombre premier p est nommé caractéristique du corps.

Formule de Gauss			haut
Formule Gauss a trouvé une belle formule pour donner la quantité de polynômes irréductibles. Il s'agit d'un corps fini de p éléments. Pour les polynômes de degré n. d sont tous les diviseurs de n. et µ est la fonction de Moebius.
Exemple Dans F₂ pour le quatrième degré. On a trouvé trois polynômes irréductibles. Le calcul de la formule confirme cette valeur.

Irréductibles sur F₃ ou GF[3]			haut
Premier degré
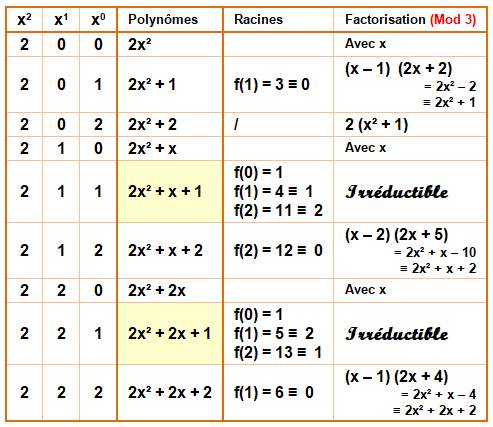
Deuxième degré En général, seuls les polynômes de coefficients 1 pour x² sont considérés (polynômes unaires). Dans le cas d'un coefficient autre pour x², un polynôme avec ce coefficient en facteur est considéré comme réductible.
Calcul Dans F₃ pour le deuxième degré. On a trouvé trois polynômes irréductibles unaires (Tableau du haut). Le calcul de la formule confirme cette valeur.