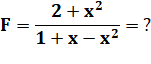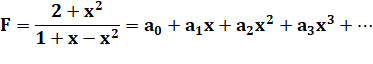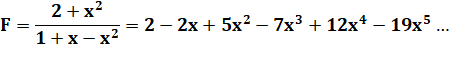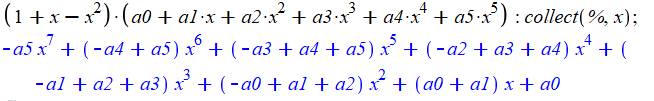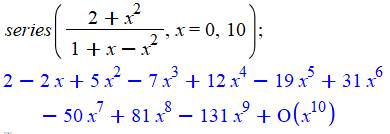|
||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DIVISION
des POLYNÔMES Vous
savez divisez les nombres. Alors,
vous savez diviser les polynômes ! En prime, trouvez le quotient sans diviser … >>> |
Voir Bases
de l'algèbre
|
Cas
simple de division par un monôme |
|
||||||||||
|
Posez la division
comme d'habitude avec les nombres. |
|
||||||||||
|
|
|
||||||||||
|
La division est
terminée |
Résultat: 3a + 1 / a = 3, reste 1 Vérification: 3 x a + 1 = 3a + 1 |
||||||||||
|
|
|
|||||||||||||||
|
Le reste est 1 et
la division est finie. |
Résultat: 3a² + 5 a + 1 / a = 3a + 5, reste 1 Vérification: 3a x a + 5 x a + 1 = 3a² + 5a + 1 |
|
|
|||||||||||||||||
|
a² + 2ab + b² par a + b. |
|
||||||||||||||||
|
|
Résultat: ( a² + 2ab + b² ) / ( a + b ) = a +
b, reste 0 Vérification: (a + b)(a + b) = a² + 2ab + b² |
||||||||||||||||
Remarque
|
Pour effectuer la division d'un polynôme
par un autre,
|
|
Lançons-nous!
et faisons une découverte miraculeuse |
|
||||||||||||||||||||||
|
En développant |
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
Formule que vous
pouvez vérifier en poursuivant les calculs. |
La division engendre la suite de tous les nombres entiers dans l'ordre et jusqu'à l'infini |
||||||||||||||||||||||
Voir Fonction
génératrices des nombres

![]()
|
|
|||||
|
Comment
trouver le développement d'une fraction polynomiale sans effectuer la
division ? |
|
||||
|
Polynôme générique |
|
||||
|
En multipliant |
|
||||
|
Développement sans les termes en x3 et au-delà. En effet, le membre de gauche n'a pas de tels
termes. |
|
||||
|
Égalité des coefficients |
|
||||
|
Les coefficients suivants du développement sont nuls. En reprenant leur valeur en ai , on calcule
la valeur de chacun des ai . |
|
||||
|
Le développement cherché |
|
||||
|
Pour information, le développement complet en ai
Notez que les coefficients ne sont complets que
jusqu'à x5. Vous remarquerez que, cependant, ils ont tous la même
allure. |
|||||
|
Calcul sans limite Maple
donne directement le résultat en utilisant l'instruction series. Ici, jusqu'à
la puissance 9:
Le O(x10) indique que la suite est en
puissance de 10 et plus. |
|||||
Voir Développements
limités / Démonstrations
semblables
![]()
|
Suite |
|
|
Retour Voir résumés en (Très utile) |
|
|
Voir |
|
|
Cette page |