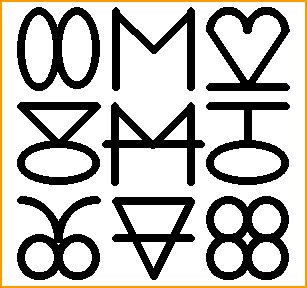|
|||||||||||||||||||||||||||||||||||
![]()
|
Symétries – Novices / Débutants La notion de symétrie est assez naturelle tant nous la
rencontrons dans la vie de tous les jours, parfois sans s'en rendre compte. C'est
le cas de notre image dans le miroir. Ou
même, en gros, la division en deux parties identiques du corps humain: la
gauche et la droite. La symétrie axiale doit être
maitrisée en fin de primaire et consolidée en classe de sixième. La symétrie
centrale est vue en cinquième. |
|
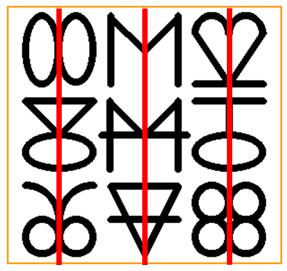
Pouvez-vous
continuez cette suite de figures en ajoutant les trois suivantes en bas ? Indice: nous sommes sur la page des symétries
et, même plus, débutants. Super indice: la figure du motif au centre est OMO. |
|
|
Remarquez que cette coccinelle présente, en
plus, les mêmes dessins sur sa partie droite comme sur sa partie gauche.
Il semble que l'on peut prendre l'une des
images, la faire pivoter d'un demi-tour et alors elle est superposable à
l'autre. Est-ce vrai ?
Le museau proche du miroir dans l'image de
gauche reste proche du miroir dans
l'image de droite. La queue éloignée reste éloignée du miroir. D'une manière générale, sur les deux images
un point identique est à égale distance du miroir.
Pour s'en rendre compte, mettez une
étiquette sur l'oreille gauche du tigre et faîtes pivoter; elle se trouvera à
droite et non à gauche comme l'original Pour réellement passer d'un animal à
l'autre, il faudrait les retourner comme un retourne un gant Tous les points de l'original passent à
travers le miroir à égale distances.
Votre main gauche reste à gauche, votre
tête reste en haut et vos pieds en
bas. On entend parfois la question suivante:
pourqio le miroir inverse la gauche et la droite et pas le haut et le bas? Vous l'avez compris désormais: c'est un
effet de la symétrie verticale de notre corps qui donne l'illusion. |
|
|
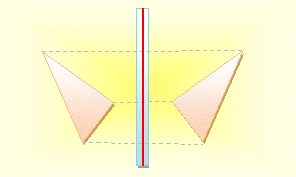
On projette chaque point vers le miroir et
on prolonge d'une longueur égale à celle déjà faite.
-
De A
menez une perpendiculaire à D -
Elle coupe D en a -
Prolongez jusqu'à A', tel que Aa = aA' -
Procédez de même avec B pour obtenir Bb = bB'
avec BB' perpendiculaire à D |
|
|
une
SYMÉTRIE
AXIALE de AB par rapport à la
droite une
SYMÉTRIE
ORTHOGONALE de AB par rapport à la droite |
|
|
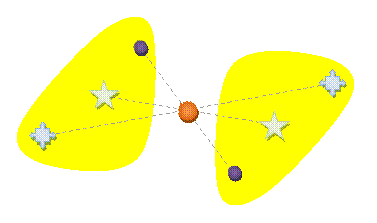
Demi-tour comme si on avait découpé l'image
du tigre et maintenu ce point à sa place par une punaise
Oui, toutes des droites se coupent au point
de rotation (point marron ou punaise)
Prendre chaque point de l'image d'origine
et le transformer en tirant une droite vers le point de rotation Ensuite, prolonger le trait d'une distance
égale à celle déjà parcourue |
|
|
On projette chaque point vers le centre et
on prolonge d'une longueur égale à celle déjà faite.
-
De A
menez une droite vers O -
Prolongez jusqu'à A', tel que AO = OA' -
Procédez de même avec B pour obtenir BO = OB' |
|
|
une
SYMÉTRIE
CENTRALE de AB par rapport à
point |
|
|
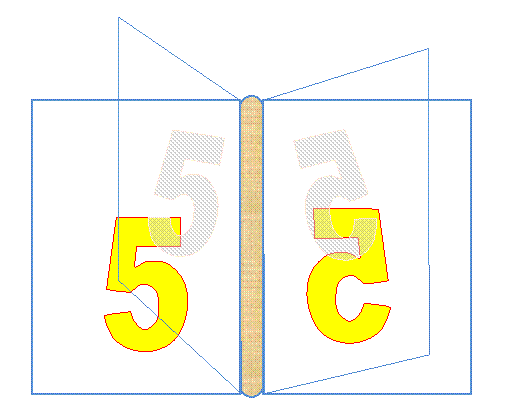
Le
chiffre 5 est retourné comme vu dans un miroir. Célèbre
façon d'écrire de Léonard de Vinci pour rendre ses textes secrets. |
|
![]()
Plus formellement
en classe de sixième – Notions et vocabulaire à maitriser
|
Approche |
|
|
|
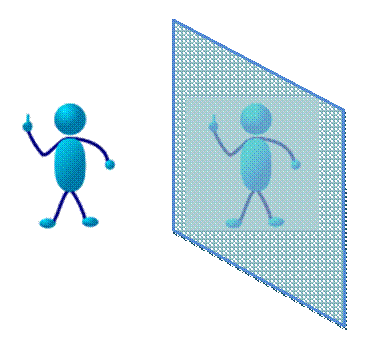
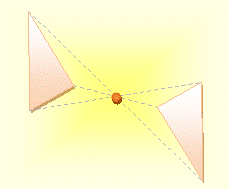
Tu es
devant un miroir. Sais-tu qui est dans ce miroir. – Ben, moi, voyons! – Non, ce n'est pas toi. – Tu rigoles. – Non! L'image que tu vois est ton symétrique. Ce n'est pas
comme cela que tous les gens autour de toi te voient. Ta
cicatrice (exemple) est à droite pour tout le monde, sauf dans le miroir où
elle est à gauche. Sur l'illustration, on montre comment se voir comme les autres nous
voient. On utilise deux miroirs positionnées à un peu moins de 90° l'un de
l'autre. L'image dans le miroir secondaire de l'image dans le miroir principal
est identique à l'original. Fais l'expérience. Ta cicatrice sera du bon côté, cette fois. |
|
|
|
Comment reconnaitre une
symétrie axiale |
|
|
|
Comment détecter
un axe de symétrie? Le truc consiste à placer une règle dans la position de
l'axe imaginé et de comparer les deux côtés. Éventuellement en tournant la
figure pour avoir la règle bien en face. Si les
deux parties sont semblables du haut vers le bas, alors c'est un axe de
symétrie. En tout cas, ce truc à donné le déclic à beaucoup
de jeunes que j'ai pu suivre. Je les voyais mettre la règle et essayer et
découvrir des axes qu'ils n'avaient pas soupçonnés. |
Oui, les bras du pingouin ne sont pas symétrique!
|
|
|
Vocabulaire – Mots-clés |
|
|
|
Symétrie (Symmetry) |
Similitude exacte des deux parties d'un espace de
part et d'autre d'un axe (symétrie axiale) ou autour d'un centre (symétrie
centrale). On dit qu'un point A est symétrique d'un point B
par rapport à une droite (d) si le segment [AB] et la droite (d) forment un
angle droit et si la droite (d) coupe le segment [AB] en son milieu. Dans ce cas, on dit qu'A est l'image de B par la
symétrie d'axe (d). Autrement dit : ' on dit qu'un point A est
symétrique d'un point B par rapport à une droite (d) si la droite (d) est la
médiatrice du segment [AB]. Deux
figures symétriques sont superposables lorsque dessinées sur un
papier-calque. |
|
|
Transformation |
Opération géométrique qui transforme une image en
une autre Chaque
point de l'image est transformé en son point image. La
réalisation d'une symétrie est une transformation. |
|
|
Médiatrice |
Droite perpendiculaire à un segment en son
milieu. Tout
point de la médiatrice est à égale distance des extrémités du segment. |
|
|
Bissectrice |
Droite qui partage un angle en deux angles égaux. Droite qui partage un secteur angulaire en deux
secteurs angulaires de même angle. Tout
point de la bissectrice est à égale distance des côtés de l'angle qu'elle
partage. |
|
|
Image |
Si deux figures, deux droites, deux points … sont
symétriques, l'une est l'image de l'autre par la symétrie considérée. |
|
|
Conservation |
Deux figures symétriques ont des composantes qui
ont les mêmes alignements et les mêmes mesures: longueurs, angles, aires. |
|
|
En
traçant trois axes de symétrie verticaux, on fait apparaitre les nombres de 0
à 8 et leurs images. Devinette
souvent plus facile à trouver par les plus jeunes. |
|
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Transfor/Symetrie/Debutant.htm |
![]()