NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/11/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Outils mathématiques
Débutants Général	GROUPES			Glossaire Symétrie
INDEX Structures algébriques	Introduction	Triangles et carrés	Groupe – Définition	Symétrie
		1D - Bande	2D - Papier peint	3D - Cristallographie
		Sommaire de cette page >>> Approche – La ronde enfantine >>> Symétrie >>> Les 4 opérations fondamentales >>> Billard en rond et symétries >>> Historique

SYMÉTRIES

Symétrie fait penser à image dans un miroir ou alors aux deux parties d'un visage ou d'un museau (voir illustration à droite). Les mathématiciens qui ont le goût de la généralisation y voient beaucoup plus. Les papiers peints et les frises de décoration sont une bonne approche des symétries. Savez-vous que le nombre de types de décorations est limité à 7 pour les frises et, à 17 pour le papier peint ? La cristallographie s'intéresse à toutes les symétries possibles en 3 dimensions.

Approche – La ronde enfantine
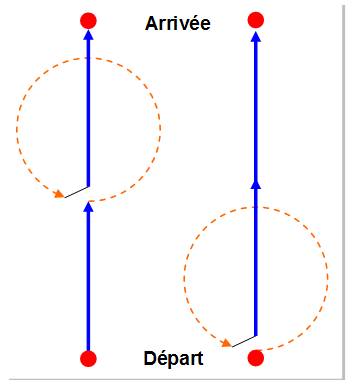
Les deux combinaisons d'opérations conduisent au même résultat.
Un pas en avant Un tour complet Un pas en avant	Un tour complet Un pas en avant Un pas en avant

Les deux combinaisons d'opérations NE conduisent PAS au même résultat.
Un pas en avant Un demi-tour complet Un pas en avant	Un demi-tour complet Un pas en avant Un pas en avant

Symétries

Avec des mouvements de base de cette sorte, on déplace le point rouge. On peut faire la même chose avec des motifs de papier peint. Les dimensions du motif sont conservées. On le transforme par déplacement (translation), par rotation, par utilisation de l'image miroir, etc. Ces mouvements de base peuvent être effectuées séparément ou en combinaison. Le nombre de combinaisons est limité. Certaines redonnent les mêmes résultats. On trouve donc des catégories de résultats, dits groupes de symétries. Le mot symétrie est utilisé au sens mathématique. Ce terme regroupe toutes les isométries possibles et pas simplement une symétrie de type miroir.

Les quatre OPÉRATIONS FONDAMENTALES
Translation (Translation) Répétition du motif	Réflexion (Reflection) Motif vu dans un miroir vertical
Réflexion glissée ^1 (Glide reflection) Motif vu dans un miroir horizontal, et décalé	Rotation (Rotation) Motif après un demi-tour
Note ^1 La réflexion est celle obtenue avec un miroir horizontal: le F image serait en bas du F de départ En fait, on le fait glisser pour le remettre dans la bande de la frise.

Billard en rond et symétries
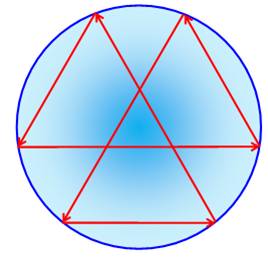
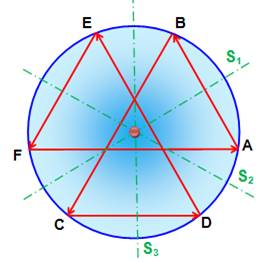
Un billard circulaire. Il se trouve que sur ce billard particulier, la boule rebondit dans une direction à 60°. Lancée de n’importe où, curieusement après le sixième rebond, la boule repasse toujours par sa trajectoire initiale. La démonstration par les symétries est élégante. On dessine en vert les axes de symétries. L’axe S1 fait passer A en B ; S2 donne C pour image de ; etc.
Pour passer de A en B on applique les six symétries successives  (on écrit les symétries dans l’ordre inverse): S = S3 . S2 . S1 . S3 . S2 .S1 Le produit de deux symétries d’axes concourants est une rotation et deux rotations de même centre sont commutatives. S = (S3 . S2) . (S1 . S3) . (S2 .S1) S = (S3 . S2) . (S2. S1) . (S1.S3) En les associant pour mettre des symétries doubles, synonymes d’identité: S = S3 . (S2. S2). (S1 . S1).S3 S = S3 . S3 = identité

Historique

Les décorations sur les bâtiments, les tissus …existent depuis longtemps. Les motifs et leurs dispositions ont été élaborés au fil du temps. C'est la cristallographie qui a conduit à déterminer toutes les manières possibles de répéter des motifs sur 3 dimensions. Ces études commencèrent au XIXe siècle. 1891 : E.S. Federov donne une liste de 230 formes possibles en 3D et 17 en 2D. 1935: H.J. Woods publie une étude sur les symétries des motifs à couleurs des textiles. 1927: G. Polya et A. Speiser, mathématiciens, rapprochent les types cristallographiques et groupes de symétries. 1952: H. Weyl publie un ouvrage devenu un classique sur les symétries. 1960: développements mathématiques sur la symétrie. 1981: J.D. Jarratt et R.L.E. Schwarzenberger publient « Colored frieze groups », et démontrent que le nombre de bandes différentes est 7 pour n impair, 17 lorsque n =- 2 (mod 4), et 19 pour n =- 0 (mod 4). 1987: H.S.M. Coxeter, dans « A simpler introduction to colored symmetry », donne une preuve simple de ces théorèmes.

Retour	Groupe - Introduction
Suite	1D - Bande Symétrie – Glossaire
Voir	DicoMot Géométrie – Index Illusions d'optique Constructions des ensembles de nombres Polyèdres Transformation Triangles
Livre	Mathématiques d'ailleurs - Marcia Ascher
Sites	The 17 Wallpaper Groups - de Xah Lee, spécialiste des groupes de symétries 17 Wall Paper Symmetry Groups to Create a Regular Division of the Plane - Hans Kuiper's Computer Art Pictures Symmetry and Tessellations - Plus de 150 sites sur la symétrie et le pavage Reflection in water -Animations Tour of Symmetry Groups - Éducation & exercices About Symmetry and Pattern - Introduction à un exposé sur les tapis
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Symetrie.htm