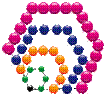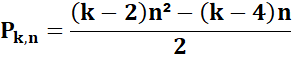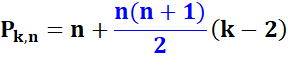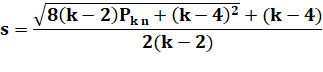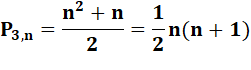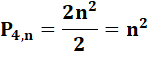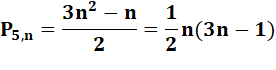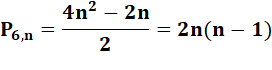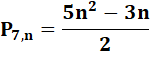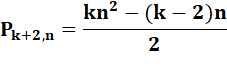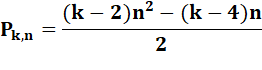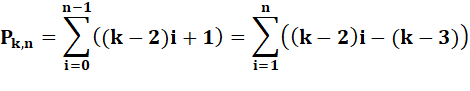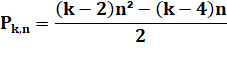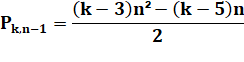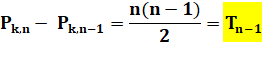|
Édition du: 18/09/2023 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
||||
|
Tables
Poly |
|||||
![]()
|
NOMBRES POLYGONAUX
Nombres
construits en déposant des points sur des polygones
gigognes. L'un s'appuyant sur les autres avec deux côtés en commun. Voir tout de suite les illustrations ou les
tables. |
||
|
|
Sommaire de cette page >>>
Caractéristiques >>>
Savoir si un nombre est k-gonal >>>
Formule >>>
Passage d'un polygonal au polygonal suivant |
Débutants Nombres figurés
ou géométriques Glossaire |
|
Famille |
Nombre / Formes |
|||||||
|
Définitions |
NOMBRE POLYGONAL (ordinaire)
|
|||||||
|
Famille |
|
|||||||
|
|
En bleu, la somme
des entiers de 1 à n.
Voir Exemple nombres
décagonaux
|
|||||||
|
Propriétés |
|
|||||||
|
Triangle de Pascal |
|
|||||||
|
Angl |
|
|||||||
|
Voir |
|
|
|
||
|
On
recherche si le nombre n est k-gonal. Prendre
ce nombre moins 2 et le multiplier par 8. |
8(k – 2) |
|
|
Multiplier
par le nombre visé |
8(k – 2)n |
|
|
Ajouter
le carré de k - 4 |
8(k – 2)n + (k – 4)² |
|
|
Si
ce nombre est un carré alors n est k-gonal |
8(k – 2)n + (k – 4)² = c² ? |
|
|
Exemples
Est-ce
que 36 est triangulaire? |
8(3 – 2) x 36 + (–1)² = 8 x 36 + 1 = 289 = 17² |
|
|
Est-ce
que 25 est carré? |
8(4 – 2) x 25 + (0)² = 16 x 25 = 20² |
|
|
Est-ce
que 210 est pentagonal? |
8(5 – 2) x 210 + (1)² = 24 x 210 + 1 = 5 041 = 71² |
|
|
|
||
|
Triangulaires |
|
|
|
Carrés |
|
|
|
Pentagonaux |
|
|
|
Hexagonaux |
|
|
|
Heptagonaux |
|
|
|
(k + 2)-gonaux |
|
|
|
k-gonaux |
|
|
|
k-gonaux (somme) |
|
|
|
Gnomon |
|
|
Complet en Nomenclature
des nombres polygonaux
|
|
||
|
Polygonal d'ordre k |
|
|
|
Polygonal d'ordre k – 1 |
|
|
|
Différence |
|
|
|
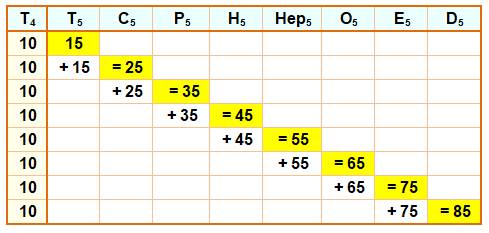
Théorème de Bachet |
On passe
d'un polygonal d'ordre k au polygonal d'ordre k + 1 en lui
ajoutant le triangulaire d'ordre k.
|
|
|
Exemple |
Voir Table
des nombres polygonaux Brève
de maths 489 |
|
Les nombres sur chaque ligne sont en progression
arithmétique.
Observez (flèches) comment, pour n = 4, on passe de 10 à 16 en ajoutant
le triangulaire précédent (6). Propriété générale.
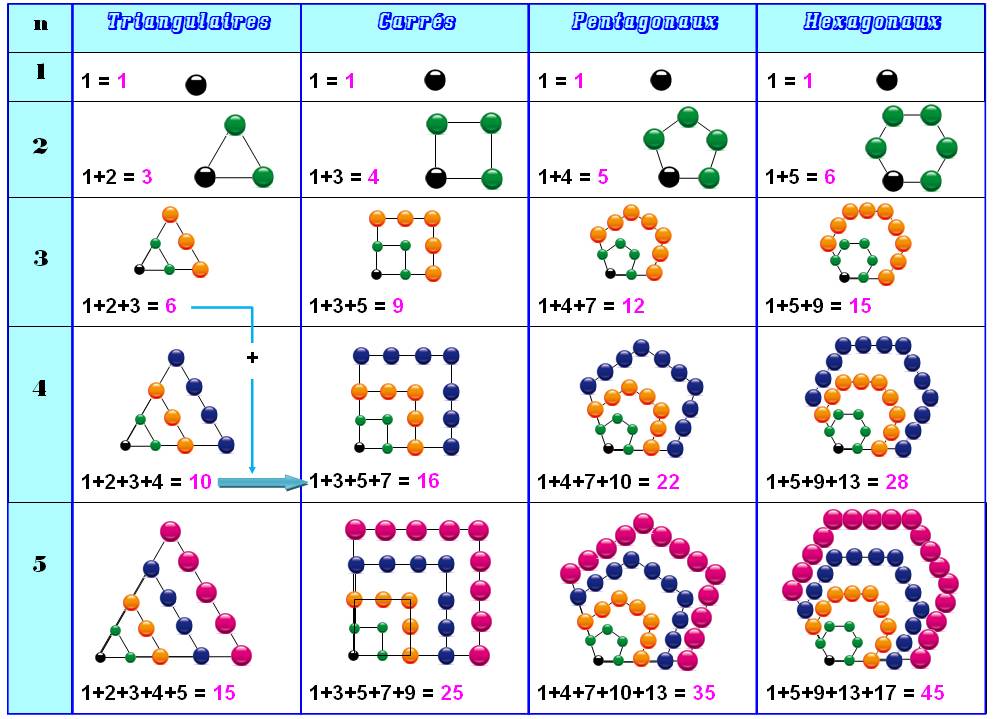
Voir Polygonaux centrés en images
/ Polygonaux simples en images / Brève 53-1053
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()