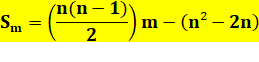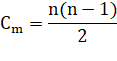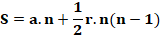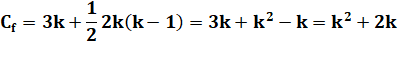|
||||||||||||||||||||||||||||||||
![]()
|
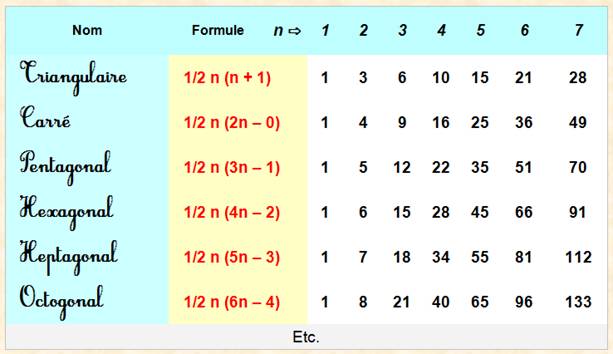
NOMBRES FIGURÉS Cas des nombres polygonaux Liste des premiers nombres
polygonaux, nombres figurés dans le plan et dont la base géométrique est un polygone
régulier. Calcul pas à pas de la
formule générale des nombres polygonaux (nième m-gonal):
Notations: sur cette page les nombres polygonaux sont notés S; la lettre P
habituelle étant réservée ici à la progression arithmétique. Un nombre
pentagonal (exemple) est un 5-gonal. En général on dit k-gonal ou, comme ici,
m-gonal. |
|
|
||
|
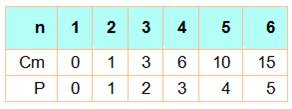
Tableau |
Notez que le
premier est toujours 1 et le deuxième est m,
la quantité de côté du polygone. |
|
|
Propriétés |
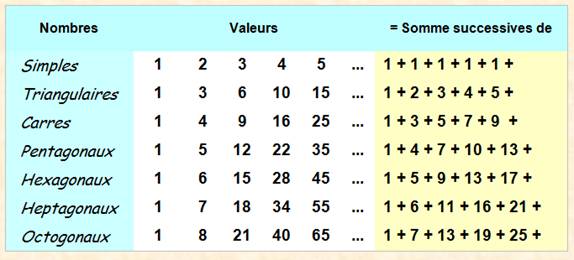
On
obtient un nombre polygonal en additionnant les premiers termes d'une suite
arithmétique >>> On
peut arranger le nombre de points en figures géométriques, d'où leur
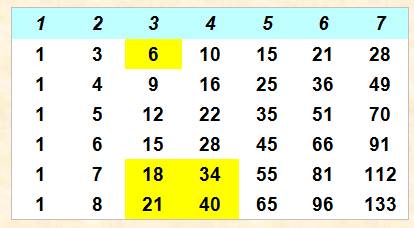
nom. Les
nombres hexagonaux sont aussi triangulaires. Les
nombres pentagonaux sont des tiers de nombres triangulaires. |
|
|
|
||||
|
Suite au chapitre ci-dessus, un nombre polygonal est
égal à son prédécesseur auquel on ajoute la raison de la progression
arithmétique. Celle-ci varie selon le type de polygone à m côtés (appelé m-gone). |
Triangulaire r = 1 Carré r
= 2 Pentagone r
= 3 m-gone r
= m – 2 |
|||
|
Formules
de récurrence pour:
|
Progression arithmétique Pm(n+1) = Pm(n) + (m –
2) Ex: P5(4) = P5(3) + 3 = 7 + 3 = 10 Rappel
calcul du terme (n+1) d'une progression arithmétique de raison (m-2)
commençant par 1: Pm(n+1) = 1 + n(m – 2) Nombre polygonal Sm(n+1)= Sm(n)
+ Pm(n+1) = Sm(n) + { 1 + (n) (m – 2)
} Sm(n+1) = Sm(n) + 1 + n(m
– 2) Ex: S5(4) = S5(3) + 1 + 3(5
– 2) = 12 + 1 + 9 = 22 |
|||
|
Formule
développée du nombre m-gonal |
Sm(n) = 1 + {1 +
(m–2)} + {1 + 2(m–2)} +… + {1 + (n–1)(m–2)} |
|||
|
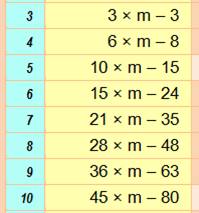
Les
premières formules Par exemple le 5e m-gonal a pour formule générale: 10m – 15. Prenons m = 5 pour les nombres pentagonaux, alors le 5e
pentagonal est 10 x 5 – 15 = 35. |
Voir Table
complète et valeurs |
|||
|
Formule
générale pour le nième m-gonal Les coefficients de m et le coefficient fixe sont en
progression arithmétique. Exemple
de calcul avec la formule 10e hexagonal: n = 10 m = 6.
S6(10)
= (10 x 9 / 2) x 6 + 10² – 2 x10 = 45
x 6 – 80 = 190 Exemple
de formule Pour les triangulaires (m = 3) S3 = ½
n(n – 1) x 3 – n² + 2n S3 = ½
(3n² – 3n – 2n² + 4n) S3 = ½ (n² + n) |
Coefficients
de m
La progression est arithmétique de raison 1 et
commençant par 0, c'est la somme des entiers
Coefficients
fixe
La progression
est arithmétique de raison r = 2 et commençant par a = 3:
Formule
générale
|
|||
|
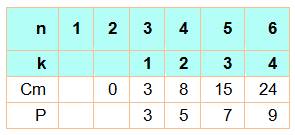
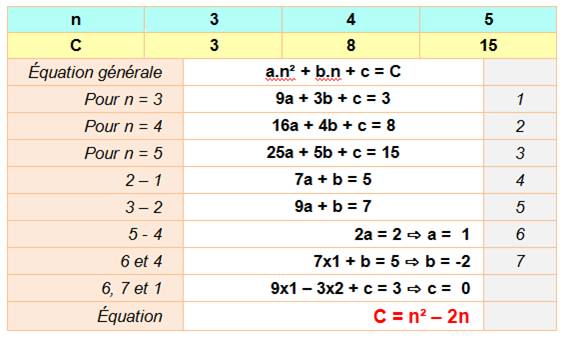
Comme
exercice Calcul des coefficients par utilisation d'un système équations |
Exemple
avec le coefficient fixe
|
|||
|
Nous avons établi la formule des nombres polygonaux par deux
voies différentes, donnant le même résultat. Extraordinaire, cette formule permet le calcul du nième nombre m-gonal quelque soit m et n.
|
|
Voir Table
des valeurs des nombres polygonaux
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Livre |
voir Conway et Guy " The book of
numbers " (Le
livre des nombres) |
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbGeome1.htm
|
![]()