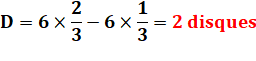|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 53 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
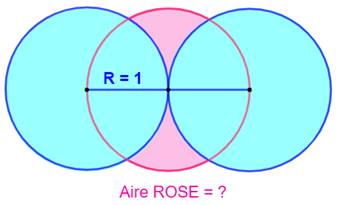
1040. Trois cercles |
|
|||
|
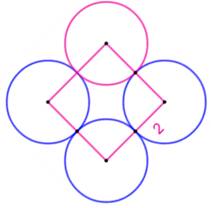
Construction Trois cercles de même rayon (R = 1) de centres
alignés. Les centres des deux cercles tangents sont les
extrémités d'un diamètre du cercle central. Quelle est l'aire de la zone rose ? Piste Construire quatre triangles équilatéraux et évaluer l'aire du disque
rose complet. Aire de la zone rose
|
|
|||
|
Brèves associées |
>>> Trois
cercles dans un rectangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Trois cercles – Solution complète |
>>>
Cercle – Index |
||
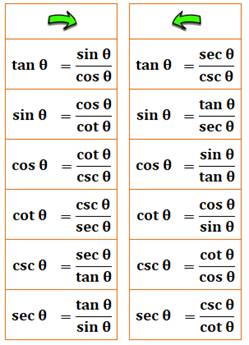
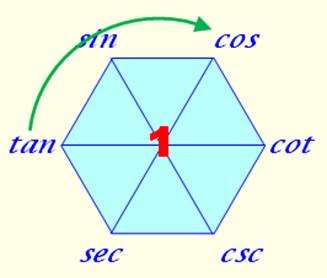
1041. Hexagone magique en trigo. |
|
|||
|
Identités quotients Voyez comme il facile de construire le tableau
par simple lecture du graphique en hexagone.
|
Bien d'autres propriétés trigonométriques sont
contenues dans ce simple hexagone … |
|||
|
Brèves associées |
>>>
Calcul avec les cosinus |
>>>
Brèves Trigonométrie – Index |
||
|
Pour en savoir plus |
>>>
Tout sur l'hexagone magique |
>>>
Fonctions trigonométriques |
||
1042. Chapelets de cercles |
|
|||
|
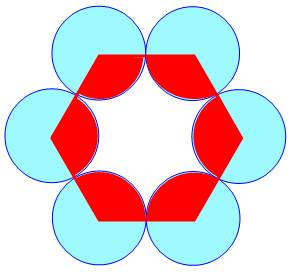
Hexagone et cercles À chaque sommet, on place un cercle centré sur le
sommet et de rayon moitié du côté de l'hexagone. Curieusement, la différence d'aires entre la zone
bleue et la zone rouge est égale à celle de deux cercles complets. Polygone quelconque et cercles La propriété est valable pour tout polygone,
régulier ou non, convexe ou non. La différence d'aires entre la zone bleue et la
zone rouge pour un polygone quelconque formé par un chapelet de cercles est
constante et égale à celle de deux disques. |
Chapelet de cercles: ils sont
tangents deux à deux et ont le même
rayon. |
|||
|
Brèves associées |
>>>
Cercles tangents |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Chapelet de cercles |
>>>
Quatre cercles |
||
1043. Théorème des angles alternés |
|
|||
|
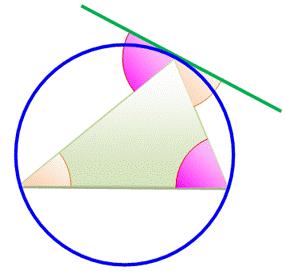
Théorème Un cercle et une tangente. Un triangle quelconque
inscrit dans le cercle. Aux sommets, les angles avec la tangente sont
égaux aux angles alternés du triangle. Explication Les angles interceptent les mêmes arcs. Or, les
angles inscrits interceptant le même arc sont égaux. |
|
|||
|
Brèves associées |
>>>
Angles autour du cercle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème des angles alternés |
>>>
Angles inscrits |
||
1044. Compter avec les doigts |
|
|||
|
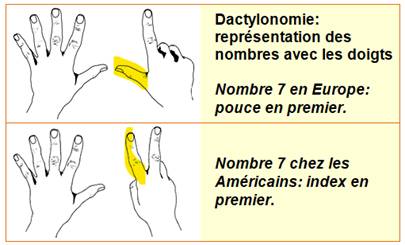
Chiffres
et doigts Notre façon de compter avec la base 10 (système
décimal) est probablement apparue parce que nous avons 10 doigts. Si nous avions évolué avec 8 ou 12 doigts, notre système
de numération aurait pu être très différent. Notez que le mot "digit", dans le sens
de chiffre, vient du latin digitus, qui signifie doigt ou orteil On sait aussi que les gens ont des techniques
très différentes pour garder la trace des chiffres sur leurs mains. |
Deux façons de compter avec les
doigts
|
|||
|
Brèves associées |
>>> Nombres cachés en français |
>>>
Brèves Sémiologie – Index |
||
|
Pour en savoir plus |
>>>
Compter avec les doigts |
>>>
Système décimal |
||
1045. Divisibilité de abc abc |
|
|||
|
Nombres en abc abc En notant que 91 x 11 = 1001 et que, d'une manière
générale, les diviseurs de 1001 sont: 1, 7, 11, 13, 77, 91, 143, 1001 on peut
établir que: Tous les nombres en par 7, 11, 13, 77, 91, 143 et 1001. La barre indique qu'il faut lire un nombre en
entier. Nombres en aba bab Il existe mieux
! Les nombres en aba bab sont divisibles par
1, 3, 7, 13, 21, 37, 39, 91, 111, 259, 273, 481, 777, 1 443, 3 367, 10 101. Ex: 121 212 / 3 367 = 36; 999 999
/ 1 443 = 693 |
Exemple avec abc = 123
Cas de 909 090, nombre en aba bab Le nombre 909
090 est exceptionnel avec 128 diviseurs. |
|||
|
Brèves associées |
>>>
Divisibilité par 137 |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Divisibilité de abc abc >>>
Nombres en 1010… et divisibilités |
>>>
Divisibilité de 909 090 et autres >>>
Diviseurs |
||
1046. Étoile cachée |
|
|||
|
Sur cette
figure, pouvez-vous identifier une étoile
à cinq branches ? Ce défi a été
imaginé par Samuel (Sam) Lyod (1841-1911), un joueur d'échecs, un auteur
d'énigmes et un expert en amusements mathématiques. |
|
|||
|
Brèves associées |
>>> Graphe pentagonal à
colorier |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Pentagone et étoile à cinq branches >>>
Sam Lyod – Biographie |
>>>
Hexagone et étoile à six branches >>> Pesée de Sam
Lyod |
||
1047. La balle plus lourde |
|
|||
|
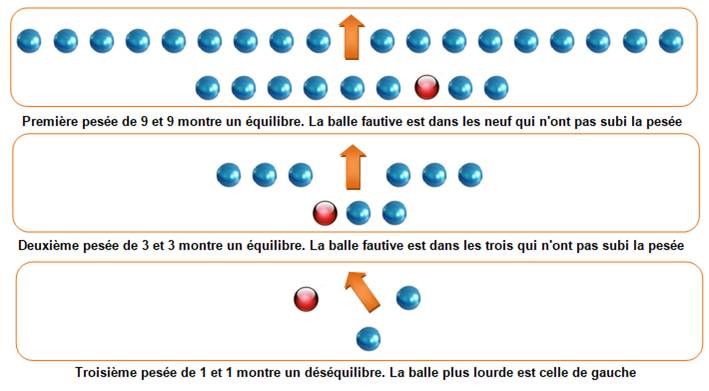
Défi Parmi ces
vingt-sept balles, l'une est plus lourde. Combien
de pesées suffisent pour la détecter ? Réponse :
3 Cet
exemple est assez simple. ll sert d'introduction à des défis de pesées plus
sérieux ! |
|
|||
|
Les trois pesées successives
|
||||
|
Brèves associées |
>>> Pesée des quatre billes |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigmes de pesées |
>>>
Autres types de pesées |
||
1048. Aire de l'urne |
|
|||
|
Construction Une urne
(rose) est dessinée à partir de quatre cercles identiques, de rayon unité,
tangents trois à trois. Quelle
est l'aire de l'urne ? Piste (figure du bas) L'épure du
dessin montre que les centres des cercles forment un carré. L'urne
est formée d'un disque posé sur un pied qui est la zone centrale des quatre
cercles. Celle-ci
est la partie évidée du carré lorsqu'on lui retire quatre quarts de cercle
(soit un cercle). Aire de
l'urne = (Aire du carré – Aire disque) + aire disque = Aire du carré = 4. Calculs (pour le plaisir)
|
L'aire de l'urne rose est égale à celle du carré. |
|||
|
Brèves associées |
>>>
Cercles dans cercles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Quatre cercles |
>>>
Défis géométriques |
||
1049. Omar Khayyam (≈1048-≈1131) |
|
|||
|
Son nom
signifie fabricant de tentes. Khayyam
était un mathématicien et un astronome exceptionnel. ll a écrit plusieurs
ouvrages, dont Problèmes d'arithmétique,
un livre sur la musique et un sur l'algèbre avant l'âge de 25 ans. En 1070 à
Samarkand en Ouzbékistan, il écrit son ouvrage le plus célèbre: Traité sur la démonstration des problèmes
d'algèbre. Khayyam a
dirigé les travaux de compilation de tables astronomiques et a également
contribué à la réforme du calendrier en 1079. Khayyam mesurait la durée de
l'année à 365,24219858156 jours. Khayyam
cherche à résoudre ce problème: trouvez un triangle rectangle ayant la
propriété que l'hypoténuse est égale à la somme d'un côté plus la hauteur à
l'hypoténuse. Ce
problème a conduit Khayyam à résoudre l'équation cubique x3 + 200x
= 20x2 + 2000 et il a trouvé une racine positive de cette cubique
en considérant l'intersection d'une hyperbole rectangulaire et d'un cercle.
Une solution numérique approchée a ensuite été trouvée par interpolation de
tables trigonométriques. Peut-être
encore plus remarquable: Khayyam
déclare que la solution de cette cubique nécessite l'utilisation de sections
coniques et qu'elle ne peut pas être résolue par la méthode de la règle et du
compas, un résultat qui ne sera pas prouvé avant 750 ans. |
Travaux
de Khayyam:
|
|||
|
Brèves associées |
>>>
Actualités 2023 |
>>>
Brèves Histoire – Index |
||
|
Pour en savoir plus |
>>>
Équation du troisième degré >>>
Construction règle et compas |
>>>
Contemporains vers 1000 >>>
Développement du binôme |
||
1050. Passage de l'autre côté |
|
|||
|
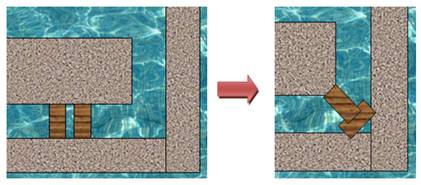
Problème (Dessin de gauche) Je suis
en bas à droite de la jetée et je dois me rendre sur le ponton central. Je ne
dispose que de deux planches qui, hélas, ne mesurent pas plus de la largeur
du gué. Comment
m'y prendre pour passer malgré tout ? Solution (Dessin de droite) Positionnez
les planches à 45° pour former une sorte de T. |
|
|||
|
Brèves associées |
>>> Trois souris sur triangle |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Traversée avec planches |
>>>
Chèvre et carré |
||
1051. Trisection des angles – Théorème |
|
|||
|
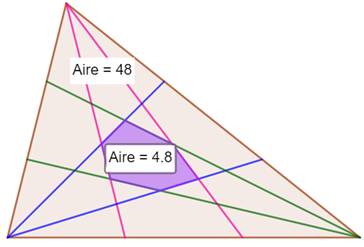
Théorème de Marion Walter – 1993 Les
trisectrices d'un triangle délimitent un hexagone interne dont l'aire est
1/10 de celle du triangle. Marion Walter (1928-2021) est une mathématicienne
allemande. Avec une
division des angles par 4, on obtient un hexagone dont l'aire vaut 8/35 fois
celle du triangle – Luca Goldoni |
|
|||
|
Brèves associées |
>>>
Triangulations des polygones |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème de Marion Walter |
>>>
Trisection des angles |
||
1052. Trisection des angles – Construction |
|
|||
|
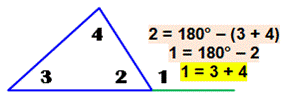
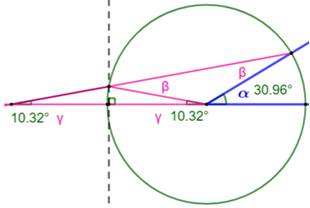
Principe Archimède imagine cette figure pour réaliser la
trisection de l'angle. Rappel
Explications (figure
du bas) Dans le grand triangle:
Dans le petit triangle rose:
Soit la valeur d'alpha:
|
L'angle gamma vaut le tiers de l'angle alpha. |
|||
|
Brèves associées |
>>> Bâton
de comptage partagé |
>>>
Brèves Histoire – Index |
||
|
Pour en savoir plus |
>>>
Trisection de l'angle >>>
Duplication du cube |
>>>
Archimède |
||
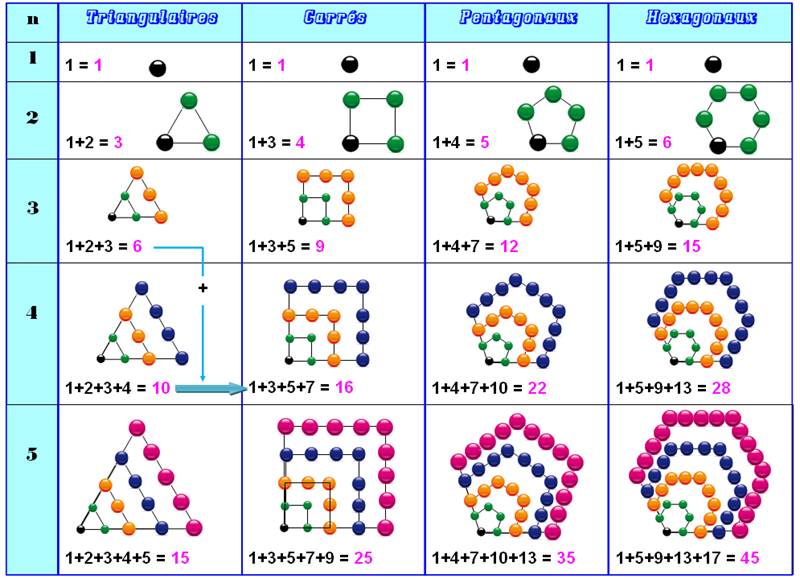
1053. Nombres polygonaux |
|
||
|
|
|||
|
Brèves associées |
>>>
Polygonaux à la courte échelle |
>>>
Brèves Histoire – Index |
|
|
Pour en savoir plus |
>>>
Nombres polygonaux |
>>>
Polygonaux centrés en images >>>
Polygonaux simples en images |
|
1054. Pesée de Sam Lyod |
|
|||
|
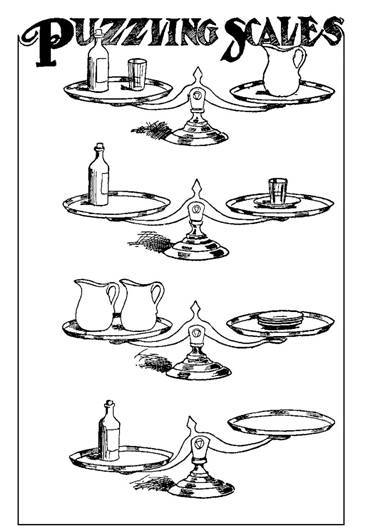
Énigme Revoici Sam Lyod pour notre
plus grand plaisir … Il nous propose trois pesées équilibrées et
demande combien de verres faudra-t-il placer sur l'autre plateau pour équilibrer
la bouteille. Le piège: bien observer
la quantité d'assiettes. Solution On écrit égalités en prenant les lettres
initiales des objets.
Il faut cinq verres pour équilibrer la bouteille. |
|
|||
|
Brèves associées |
>>> Pesée des neuf billes |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigmes de pesées |
>>>
Énigmes virales sur le Net |
||
1055. Combien de rectangles ? |
|
|||
|
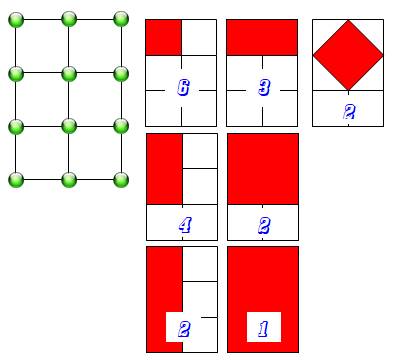
Énigme Une grille 2 x 3 comporte douze points. Combien de rectangles peut-on former avec ces
douze points ? Piste Non, ce n'est pas 18 rectangles. Il faut en
trouver deux de plus. Oui … en travers, avec les diagonales. Solution En comptant les rectangles rouges dans leurs
positions variées: |
|
|||
|
Brèves associées |
>>> Rectangle divisé en neuf |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Compter les rectangles |
>>>
Compter les triangles |
||
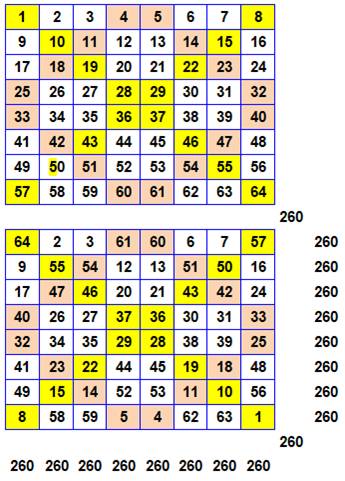
1056. Carré magique 8x8 |
|
|||
|
Construction Une grille
8 x 8 Les nombres de 1 à 64 (=8²) sont disposés dans la
grille en séquence, comme indiqué dans la grille du haut. On marque les diagonales (jaunes) et les
sou-diagonales (marron). Remplacer chacun des nombres des cases colorées
par son complément à 65. Ainsi le 1 devient 65 – 1 = 64. On observe une sorte d'inversion symétrique des
nombres. Calcul de la somme magique La somme magique est 260. C'est la somme des
nombres de 1 à 64 (=64 x 65 / 2 = 2 080), divisée par 8 lignes ou colonnes: 2
080 / 8 = 260. |
|
|||
|
Brèves associées |
>>> Carré
magique 6x6 – Construction |
>>>
Brèves Carrés magiques – Index |
||
|
Pour en savoir plus |
>>>
Carré magique 8 x 8 |
>>>
Carrés magiques – Index |
||
1057. Grenouille et cheval |
|
|||
|
Illusion d'optique ou trompe-l'œil. Très peu de gens arrive à voir un cheval sur ce
dessin montrant une grenouille Indice L'œil du cheval se trouve vers le centre de
l'image |
|
|||
|
Brèves associées |
>>> Rien –
Raymond Devos |
>>>
Brèves Humour – Index |
||
|
Pour en savoir plus |
>>>
Illusions d'optique |
>>>
Humour – Index |
||
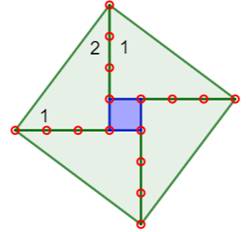
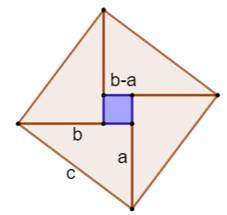
1058. Longueur de l'hypoténuse ? |
|
|||
|
Question On dispose d'un triangle rectangle dont les côtés
de l'angle droit mesurent 3cm et 4cm. Quelle est la longueur du troisième côté,
l'hypoténuse ? Piste On assemble quatre tels triangles de la manière
indiquée sur la figure. Les angles 1 et 2 sont complémentaires. Les
angles du grand carré sont donc des angles droits. Les côtés des triangles sont égaux deux à deux.
Alors, le quadrilatère vert est un carré. Un carré de côté unité est formé au centre. Calculs Aire du grand carré: 4T + 1C = 4 × (1/2×3×4) + 1 = 25 Son côté mesure: √25 = 5 Théorème de Pythagore On retrouve de théorème pour un cas particulier: Mais, celui-ci peut être généralisé en prenant a,
b et c pour côtés du triangle rectangle: |
Ce calcul figure dans un livre chinois (Chou-pei
Suan) qui date de 300 av. J.-C, environ.
|
|||
|
Brèves associées |
>>> Th.
de Pythagore – Réciproque |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème de Pythagore |
>>>
Triangle 3-4-5 |
||
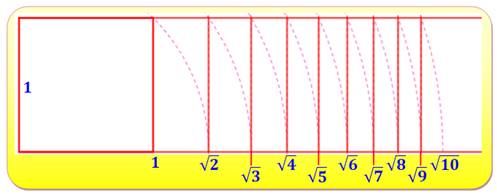
1059. Racines des nombres |
|
|||
|
Construction Carré unité. Arc de cercle avec la diagonale pour rayon. L'intersection en bas
produit la racine de 2 (longueur de la diagonale du carré unité). Etc. |
|
|||
|
Brèves associées |
>>>
Constante Pi – Formules |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Construction des racines des nombres |
>>>
Nombres et leurs représentations |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()

Solution de l'illusion grenouille cheval
Une rotation de 90°
suffit pour visualiser la tête de cheval