|
||||||||||||||||||||||||||||
![]()
|
|
||||
|
Famille |
||||
|
Définitions |
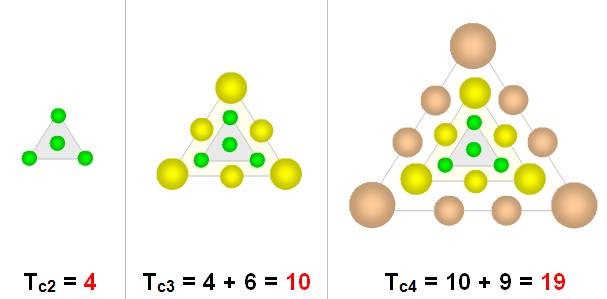
NOMBRE TRIANGULAIRE CENTRÉ
un
de plus pour chaque côté. |
|||
|
Illustr |
|
|||
|
Formule |
|
|||
|
Propriétés |
|
|||
|
Angl |
|
|||
|
Voir |
|
|||
|
|
||||
|
n P 1 1
2 4
3 10 4 19 5 31 6 46 7 64 8 85 9 109 10 136 11 166 12 199 13 235
14 274 15 316 16 361 17 409 18 460 19 514 20 571 21
631 22 694 23 760 24 829 |
25 901 26 976 27 1 054 28 1 135 29 1 219 30 1 306 31 1 396 32 1 489 33 1 585 34 1 684 35 1 786 36 1 891 37 1 999 38 2 110 39 2 224 40 2 341 41 2 461 42 2 584
43 2 710 44 2 839 45 2 971 46 3 106 47 3 244 48 3 385 49 3 529
|
50 3 676 51 3 826 52 3 979 53 4 135 54 4 294 55 4 456 56 4 621 57 4 789 58 4 960 59 5 134 60 5 311 61 5 491 62 5 674 63 5 860
64 6 049 65 6 241 66 6 436 67 6 634 68 6 835 69 7 039 70 7 246 71 7 456 72 7 669 73 7 885 74 8 104 |
75 8 326 76 8 551 77 8 779 78 9 010
79 9 244 80 9 481 81 9 721 82 9 964 83 10 210
84 10 459
85 10 711
86 10 966
87 11 224
88 11 485
89 11 749
90 12 016
91 12 286
92 12 559
93 12 835
94 13 114
95 13 396
96 13 681
97 13 969
98 14 260
99 14 554
100 14 851
101 15 151
… |
|
|
|
|||
|
La somme des n premiers nombres triangulaires
centrés donnent la constante du carré
magique d'ordre n. La formule de la constante magique est donné par: |
|
||
|
|
||||||||||||||||||||||||||||||||||||
|
Un
nombre triangulaire centré est la somme de trois nombres triangulaires: celui
de même rang et les deux précédents. |
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Divisé par 3, un nombre triangulaire centré donne un
quotient égal au nombre triangulaire de même rang et un reste de 1. Exemple: 19 = 3 x 6 + 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
![]()