|
|||||||||||||||||||||||||||||
![]()
|
ÉNIÈMES
racines de 2 La racine carrée est bien
connue: 1,4142 … Quelles les valeurs des racines cubiques, quartiques? Combien y en a-t-il?
|
|
Racine
quatrième |
|
|
|
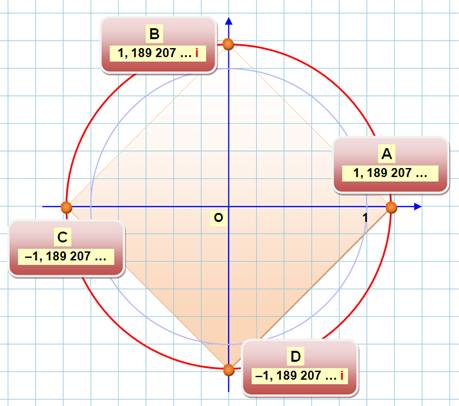
Quatre valeurs à la puissance
4 donnent 2. 1, 189 …
4 = 2 – 1, 189 … 4
= 2 ( 1, 189 … i) 4 = 2 (– 1, 189 … i) 4 = 2 Positionnés sur un système
d'axes, ces nombres forment le carré ABCD. |
|
|
|
L'équation x4 = 2 a donc
quatre racines. Les symétries du carré sont
nombreuses. Les points peuvent être échangés.
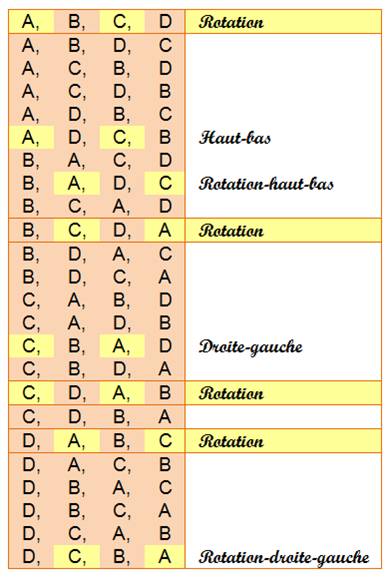
Il y a 4! = 24 permutations
possibles. Seules huit permutations
conservent les propriétés des racines. En fait, le point A doit
faire face à C (cellule en jaune), tout comme B à D. C'est le cas des quatre
permutations circulaires qui correspondent à une rotation du carré (ligne encadrée
en rouge). Deux symétries consistent à faire
pivoter le carré le haut vers le bas et, la gauche vers la droite. Les deux dernières sont
identiques avec en plus une rotation d'un quart de tour. |
A et C sont deux
racines réelles. B et D sont deux
raines imaginaires. Les racines présentent
des symétries en mimétisme avec celles du carré.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()