|
Édition du: 01/10/2021 |
|
INDEX |
Nombres premiers |
||
|
Cube (cuban) |
|||
|
Multi-Premier (C) |
|||
|
Multi-Premier (M) |
|||
![]()
|
MULTI PREMIERS par modification des leurs chiffres Quels sont les
nombres premiers
obtenus par permutations
des chiffres
d'un nombre
? Et s'il est premier lui-même ? Quels sont les records ? Exemple: le
nombre 107 "contient" cinq nombres premiers: 7, 17, 71, 107 et 701 dont deux (107 et 701) sont des anagrammes complètes. Types de nombres
multi-premiers particuliers: Premier
absolu, Emirp,
Primevals |
||
|
|
Sommaire de cette page >>>
Types de nombres multi-premiers >>>
Liste de Jamais-Premier M >>>
Liste de Multi-Premier M |
Débutants Glossaire |
Anglais:
Unprimeable number
|
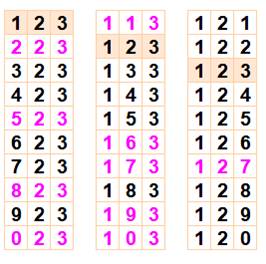
Multi-Premier M (MPM) Il s'agit de considérer tous les nombres formés
en modifiant l'un des chiffres tout en conservant les autres. Avec un nombre à trois chiffres distincts comme
123, il y a 28 nombres possibles (le nombre 123 se retrouve trois fois dans
le tableau). En rose, les dix nombres premiers. Le nombre 123
est un multi-premier par modification
d'ordre 10 (MPM10). |
|
|
|
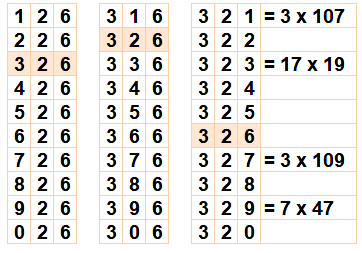
Composés stables ou Il existe des nombres pour lesquels aucune configuration
n'est première. C'est le cas de cet exemple avec le nombre 326. Toutes les configurations avec 6 pour unité sont
divisibles par 2. Dans la colonne de droite, outre les nombres
divisibles par 2 et 5, il reste 4 nombres qui s'avèrent, eux-aussi, composés. |
|
|
|
Jamais-Premier M (JPM) Le plus
petit est 200. Ils sont 95 jusqu'à 1 500. Il y en a une infinité (prouvé). Anglais: Prime-proof
numbers |
200,
204, 206, 208, 320, 322, 324, 325, 326, 328, 510, 512, 514, 515, 516, 518,
530, 532, 534, 535, 536, 538, 620, 622, 624, 625, 626, 628, 840, 842, 844,
845, 846, 848, 890, 892, 894, 895, 896, 898, 1070, 1072, 1074, 1075, 1076,
1078, 1130, 1132, 1134, 1135, 1136, 1138, 1140, 1142, 1144, 1145, 1146, 1148,
1260, 1262, 1264, 1265, 1266, 1268, 1330, 1332, 1334, 1335, 1336, 1338, 1340,
1342, 1344, 1345, 1346, 1348, 1350, 1352, 1354, 1355, 1356, 1358, 1410, 1412,
1414, 1415, 1416, 1418, 1460, 1462, 1464, 1465, 1466, 1468, 1500, … |
|
Voir Brève
721
|
Multi-Premier M (MPM) Pour les nombres de 1 à 205 |
Lecture Nombre n, quantité de premiers, ces nombres premiers Exemple Pour 10, il y a quatre possibilités de former des nombres premiers en
modifiant l'un des chiffres de 10. Ce sont: {11, 13,
17, 19}. |
||
|
1, 4, {2, 3, 5, 7} 2, 4, {2, 3, 5, 7} 3, 4, {2, 3, 5, 7} 4, 4, {2, 3, 5, 7} 5, 4, {2, 3, 5, 7} 6, 4, {2, 3, 5, 7} 7, 4, {2, 3, 5, 7} 8, 4, {2, 3, 5, 7} 9, 4, {2, 3, 5, 7} 10, 4, {11, 13, 17, 19} 11, 8, {11, 13, 17, 19, 31,
41, 61, 71} 12, 5, {2, 11, 13, 17, 19} 13, 10, {3, 11, 13, 17, 19,
23, 43, 53, 73, 83} 14, 4, {11, 13, 17, 19} 15, 5, {5, 11, 13, 17, 19} 16, 4, {11, 13, 17, 19} 17, 9, {7, 11, 13, 17, 19,
37, 47, 67, 97} 18, 4, {11, 13, 17, 19} 19, 8, {11, 13, 17, 19, 29,
59, 79, 89} 20, 2, {23, 29} 21, 7, {11, 23, 29, 31, 41,
61, 71} 22, 3, {2, 23, 29} 23, 8, {3, 13, 23, 29, 43,
53, 73, 83} 24, 2, {23, 29} 25, 3, {5, 23, 29} 26, 2, {23, 29} 27, 8, {7, 17, 23, 29, 37,
47, 67, 97} 28, 2, {23, 29} 29, 6, {19, 23, 29, 59, 79,
89} 30, 2, {31, 37} 31, 6, {11, 31, 37, 41, 61,
71} 32, 3, {2, 31, 37} 33, 9, {3, 13, 23, 31, 37,
43, 53, 73, 83} 34, 2, {31, 37} 35, 3, {5, 31, 37} 36, 2, {31, 37} 37, 7, {7, 17, 31, 37, 47,
67, 97} 38, 2, {31, 37} 39, 7, {19, 29, 31, 37, 59,
79, 89} 40, 3, {41, 43, 47} 41, 7, {11, 31, 41, 43, 47,
61, 71} 42, 4, {2, 41, 43, 47} 43, 9, {3, 13, 23, 41, 43,
47, 53, 73, 83} 44, 3, {41, 43, 47} 45, 4, {5, 41, 43, 47} 46, 3, {41, 43, 47} 47, 8, {7, 17, 37, 41, 43,
47, 67, 97} 48, 3, {41, 43, 47} 49, 8, {19, 29, 41, 43, 47,
59, 79, 89} 50, 2, {53, 59} 51, 7, {11, 31, 41, 53, 59,
61, 71} 52, 3, {2, 53, 59} 53, 8, {3, 13, 23, 43, 53,
59, 73, 83} 54, 2, {53, 59} 55, 3, {5, 53, 59} 56, 2, {53, 59} 57, 8, {7, 17, 37, 47, 53,
59, 67, 97} 58, 2, {53, 59} 59, 6, {19, 29, 53, 59, 79,
89} 60, 2, {61, 67} 61, 6, {11, 31, 41, 61, 67,
71} 62, 3, {2, 61, 67} 63, 9, {3, 13, 23, 43, 53,
61, 67, 73, 83} 64, 2, {61, 67} 65, 3, {5, 61, 67} 66, 2, {61, 67} 67, 7, {7, 17, 37, 47, 61,
67, 97} 68, 2, {61, 67} 69, 7, {19, 29, 59, 61, 67,
79, 89} 70, 3, {71, 73, 79} 71, 7, {11, 31, 41, 61, 71,
73, 79} 72, 4, {2, 71, 73, 79} 73, 9, {3, 13, 23, 43, 53,
71, 73, 79, 83} 74, 3, {71, 73, 79} 75, 4, {5, 71, 73, 79} 76, 3, {71, 73, 79} 77, 9, {7, 17, 37, 47, 67,
71, 73, 79, 97} 78, 3, {71, 73, 79} 79, 7, {19, 29, 59, 71, 73,
79, 89} 80, 2, {83, 89} 81, 7, {11, 31, 41, 61, 71,
83, 89} 82, 3, {2, 83, 89} 83, 8, {3, 13, 23, 43, 53,
73, 83, 89} 84, 2, {83, 89} 85, 3, {5, 83, 89} 86, 2, {83, 89} 87, 8, {7, 17, 37, 47, 67,
83, 89, 97} 88, 2, {83, 89} 89, 6, {19, 29, 59, 79, 83,
89} 90, 1, {97} 91, 6, {11, 31, 41, 61, 71,
97} 92, 2, {2, 97} 93, 8, {3, 13, 23, 43, 53,
73, 83, 97} 94, 1, {97} 95, 2, {5, 97} 96, 1, {97} 97, 6, {7, 17, 37, 47, 67,
97} 98, 1, {97} 99, 6, {19, 29, 59, 79, 89,
97} 100, 4, {101, 103, 107, 109} 101, 11, {101, 103, 107,
109, 131, 151, 181, 191, 401, 601, 701} 102, 5, {2, 101, 103, 107,
109} 103, 10, {3, 101, 103, 107,
109, 113, 163, 173, 193, 503} 104, 4, {101, 103, 107, 109} 105, 5, {5, 101, 103, 107,
109} 106, 4, {101, 103, 107, 109} 107, 13, {7, 101, 103, 107,
109, 127, 137, 157, 167, 197, 307, 607, 907} 108, 4, {101, 103, 107, 109} 109, 12, {101, 103, 107,
109, 139, 149, 179, 199, 409, 509, 709, 809} 110, 1, {113} 111, 11, {11, 101, 113, 131,
151, 181, 191, 211, 311, 811, 911} 112, 1, {113} 113, 8, {13, 103, 113, 163,
173, 193, 313, 613} 114, 1, {113} 115, 1, {113} |
116, 1, {113} 117, 10, {17, 107, 113, 127,
137, 157, 167, 197, 317, 617} 118, 1, {113} 119, 11, {19, 109, 113, 139,
149, 179, 199, 419, 619, 719, 919} 120, 1, {127} 121, 9, {101, 127, 131, 151,
181, 191, 421, 521, 821} 122, 1, {127} 123, 10, {23, 103, 113, 127,
163, 173, 193, 223, 523, 823} 124, 1, {127} 125, 1, {127} 126, 1, {127} 127, 9, {107, 127, 137, 157,
167, 197, 227, 727, 827} 128, 1, {127} 129, 10, {29, 109, 127, 139,
149, 179, 199, 229, 829, 929} 130, 3, {131, 137, 139} 131, 11, {31, 101, 131, 137,
139, 151, 181, 191, 331, 431, 631} 132, 3, {131, 137, 139} 133, 11, {103, 113, 131,
137, 139, 163, 173, 193, 233, 433, 733} 134, 3, {131, 137, 139} 135, 3, {131, 137, 139} 136, 3, {131, 137, 139} 137, 11, {37, 107, 127, 131,
137, 139, 157, 167, 197, 337, 937} 138, 3, {131, 137, 139} 139, 11, {109, 131, 137,
139, 149, 179, 199, 239, 439, 739, 839} 140, 1, {149} 141, 11, {41, 101, 131, 149,
151, 181, 191, 241, 541, 641, 941} 142, 1, {149} 143, 10, {43, 103, 113, 149,
163, 173, 193, 443, 643, 743} 144, 1, {149} 145, 1, {149} 146, 1, {149} 147, 12, {47, 107, 127, 137,
149, 157, 167, 197, 347, 547, 647, 947} 148, 1, {149} 149, 7, {109, 139, 149, 179,
199, 349, 449} 150, 2, {151, 157} 151, 8, {101, 131, 151, 157,
181, 191, 251, 751} 152, 2, {151, 157} 153, 12, {53, 103, 113, 151,
157, 163, 173, 193, 353, 653, 853, 953} 154, 2, {151, 157} 155, 2, {151, 157} 156, 2, {151, 157} 157, 12, {107, 127, 137,
151, 157, 167, 197, 257, 457, 557, 757, 857} 158, 2, {151, 157} 159, 11, {59, 109, 139, 149,
151, 157, 179, 199, 359, 659, 859} 160, 2, {163, 167} 161, 11, {61, 101, 131, 151,
163, 167, 181, 191, 461, 661, 761} 162, 2, {163, 167} 163, 10, {103, 113, 163,
167, 173, 193, 263, 463, 563, 863} 164, 2, {163, 167} 165, 2, {163, 167} 166, 2, {163, 167} 167, 11, {67, 107, 127, 137,
157, 163, 167, 197, 367, 467, 967} 168, 2, {163, 167} 169, 10, {109, 139, 149,
163, 167, 179, 199, 269, 569, 769} 170, 2, {173, 179} 171, 11, {71, 101, 131, 151,
173, 179, 181, 191, 271, 571, 971} 172, 2, {173, 179} 173, 10, {73, 103, 113, 163,
173, 179, 193, 373, 673, 773} 174, 2, {173, 179} 175, 2, {173, 179} 176, 2, {173, 179} 177, 13, {107, 127, 137,
157, 167, 173, 179, 197, 277, 577, 677, 877, 977} 178, 2, {173, 179} 179, 9, {79, 109, 139, 149,
173, 179, 199, 379, 479} 180, 1, {181} 181, 7, {101, 131, 151, 181,
191, 281, 881} 182, 1, {181} 183, 12, {83, 103, 113, 163,
173, 181, 193, 283, 383, 683, 883, 983} 184, 1, {181} 185, 1, {181} 186, 1, {181} 187, 11, {107, 127, 137,
157, 167, 181, 197, 487, 587, 787, 887} 188, 1, {181} 189, 8, {89, 109, 139, 149,
179, 181, 199, 389} 190, 4, {191, 193, 197, 199} 191, 11, {101, 131, 151,
181, 191, 193, 197, 199, 491, 691, 991} 192, 4, {191, 193, 197, 199} 193, 10, {103, 113, 163,
173, 191, 193, 197, 199, 293, 593} 194, 4, {191, 193, 197, 199} 195, 4, {191, 193, 197, 199} 196, 4, {191, 193, 197, 199} 197, 13, {97, 107, 127, 137,
157, 167, 191, 193, 197, 199, 397, 797, 997} 198, 4, {191, 193, 197, 199} 199, 10, {109, 139, 149,
179, 191, 193, 197, 199, 499, 599} 200, 0, {} 201, 9, {101, 211, 241, 251,
271, 281, 401, 601, 701} 202, 1, {2} 203, 8, {3, 103, 223, 233,
263, 283, 293, 503} 204, 0, {} 205, 1, {5} |
||
|
Exemple de "grosse"
production 357, 14, {157,
257, 307, 317, 337, 347, 353, 359, 367, 397, 457, 557, 757, 857} 11487, 19,
{1487, 10487, 11087, 11287, 11437, 11447, 11467, 11483, 11489, 11497, 11587,
11887, 11987, 12487, 13487, 16487, 21487, 51487, 61487} 14421, 19,
{4421, 12421, 13421, 14221, 14321, 14401, 14411, 14423, 14431, 14461, 14621,
14821, 16421, 19421, 24421, 34421, 54421, 84421, 94421} 42189, 20,
{22189, 32189, 40189, 41189, 42089, 42139, 42169, 42179, 42181, 42187, 42589,
42689, 42989, 43189, 44189, 47189, 52189, 62189, 82189, 92189} |
|||
![]()
|
Retour et suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/MultiPMo.htm
|