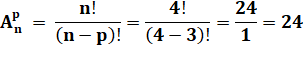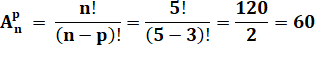NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/11/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Compter	ARRANGEMENTS			Glossaire Combinatoire
INDEX Combinatoire		Général	Exemples	La moto
		Sommaire de cette page >>> Moteur de moto et son allumage >>> Cas 3 x 3 >>> Cas 3 x 4 >>> Cas 3 x 5

ARRANGEMENTS – Exemple

Allumage de la moto

Moteur de moto et son allumage
Il s'agit de faire fonctionner une moto à six cylindres, qui a trois modules d'allumage électronique et trois capteurs. Quels sont tous les essais à faire pour vérifier le fonctionnement de tous les capteurs avec tous les modules ? Une moto ayant trois capteurs magnétiques (P, Q, R), et trois modules électroniques (1, 2, 3) qui commandent les bougies. Il semble que certains capteurs fonctionnent avec certains modules mais pas tous. 1) On voudrait faire un essai exhaustif de toutes les combinaisons possibles de trois capteurs vers trois modules. Combien d'essais possibles ? 2) On dispose d'un 4^e module (C). Combien d'essais à faire pour tester les trois capteurs avec trois modules pris parmi quatre ?

Cas trois départs pour trois destinations
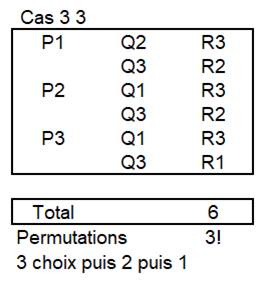
Le tableau montre les six possibilités de branchement. Le capteur P est relié au module 1, 2 ou 3, soit trois cas (P1, P2 et P3). Une fois ce choix effectué, il reste deux possibilités de branchements pour le capteur Q, soit deux choix pour chaque choix de P: 3 x 2 cas possibles. Quant au dernier capteur, il est branché sur le module restant: 3 x 2 x 1 = 6 cas possibles. Avec autant de départs (n) que d'arrivées, il s'agit de la permutation des câbles. Dans ce cas, il y a n! possibilités.

Illustration des six types de branchements

Cas trois départs pour quatre destinations
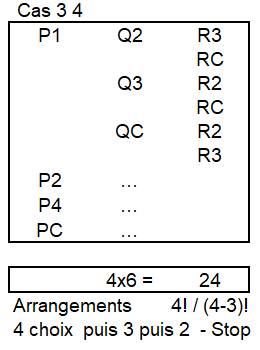
Le 4^e module étant nommé C, le tableau montre les 24 possibilités de branchement. Le capteur P est relié au module 1, 2, 3 ou C, soit quatre cas. Une fois ce choix effectué, il reste trois possibilités de branchements pour le capteur Q, soit trois choix pour chaque choix de P: 4 x 3 cas possibles. Quant au dernier capteur, il est branché sur un des deux modules restants: 4 x 3 x 2 = 24 cas possibles. Il s'agit ici des arrangements de p câbles parmi n:

Cas trois départs pour cinq destinations
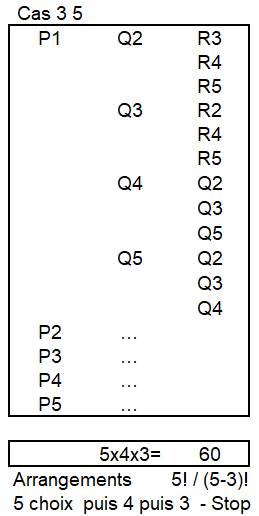
Avec cinq destinations notées (1, 2, 3, 4, 5), il s'agit des arrangements de 3 câbles parmi 5:

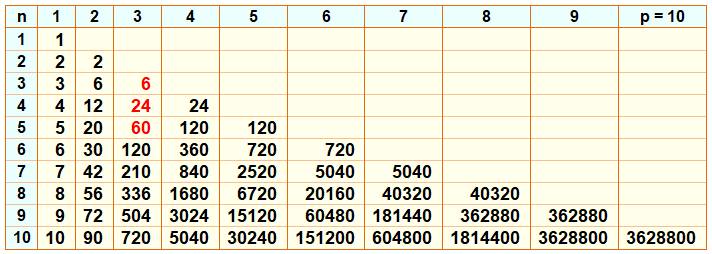
Table des valeurs pour n et p de 1 à 10

En rouge, les trois cas vus ci-dessus (n = 3, 4, ou 5 et p = 3)

Merci à Jean-Paul Corbier pour l'idée de cette page

Suite	Arrangements Willow – Énigme
Voir	Combinatoire – Index Factorielles
Cette page	http://villemin.gerard.free.fr/Denombre/ArraMoto.htm