|
||||||||||||||||||||||||||||||||||||
![]()
|
FACTORIELLES Index et introduction
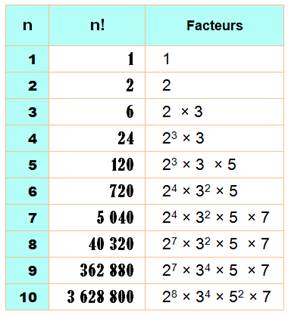
Factorielle n, avec n un entier naturel, est notée n! (1808 –
Christian Kramp). Sa valeur est le produit de tous les entiers de 1 à n. n! = 1 x 2
x 3 x … x n 5! = 1 x
2 x 3 x 4 x 5 = 120 Extraordinaire: 40 585 = 4! + 0! + 5! + 8! + 5! Trouvé en 1964 À partir de 2!, tous les nombres factoriels sont pairs. La quantité
de permutations de n
objets est égale à factorielle n. Il existe de nombreuses variantes
impliquant le produit des nombres successifs d'une suite: factorielle de premiers, de Fibonacci
… Relation fondamentale: 10! = 10
x 9! => n! = n (n –
1)! ou (n + 1)! = (n + 1) n! |
Vocabulaire
|
Une
factorielle (nom féminin): nombre notée n! Un
nombre premier factoriel, une valeur factorielle (adjectif). Anglais: factorial; Espagnol: factorial; Italien: fattoriale; Allemand: Facultät. |
Quelle est la suite ?
|
Réponse:
120 = 5!. Chaque nombre est
suivi de sa factorielle. Après 4, on trouve 4! = 24. |
|
|
||||||||||||||||||
|
Factorielles & ses formes variées |
|
|||||||||||||||||
|
||||||||||||||||||
|
Les
factorielles en question sont en fait les factorielles
|
||||||||||||||||||
|
Forme |
||||||||||||||||||
|
Relations |
|
|||||||||||||||||
![]()
|
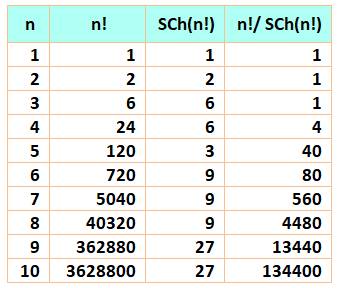
Notations On trouve
aussi: la somme cumulée des factorielles,
parfois notée !!n Exemple:
!!4 = 0! +
1! + 2! + 3! = 10. |
Note: pour avoir le symbole dièse: Alt étant
enfoncé, tapez 9839 et lâchez; pour bémol, idem avec 9836
![]()
|
Calculs |
|
||||||||||||||||
|
|
|||||||||||||||||
|
|
|
Quel
est le dernier chiffre du produit suivant: 1
x 2 x 3 x 4 x 5 … x 257 |
![]()
Une idée
des factorielles
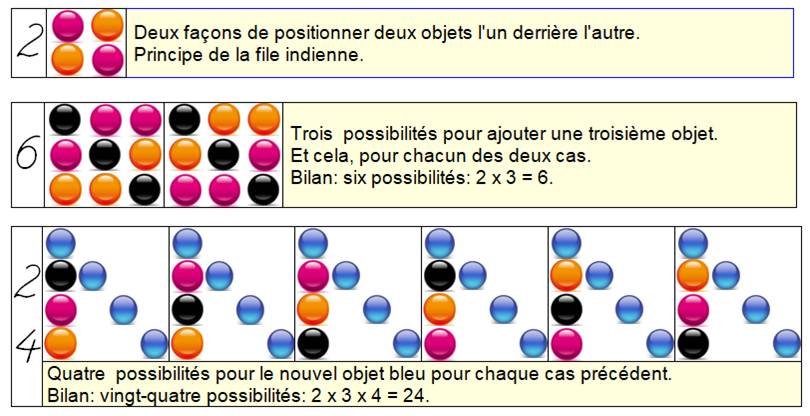
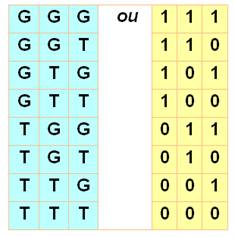
Dans le troisième tableau, les objets
noirs rouges et orange ne sont pas répétés.
Ils sont disposés dans l'ordre du
représentant figurant dans la première colonne.
Voir Les nombres
factoriels par Nathan 8 ans

Voir Brève
692
![]()
|
|
||
|
|
|
|
|
Quantité de permutations sur un banc: n! |
||
|
|
|
|
Quantité de permutations autour d'une table ronde: (n – 1)! |
|
|
|
|
Voir Dénombrement
– vue générale / Problème des
places assises autour d'une table
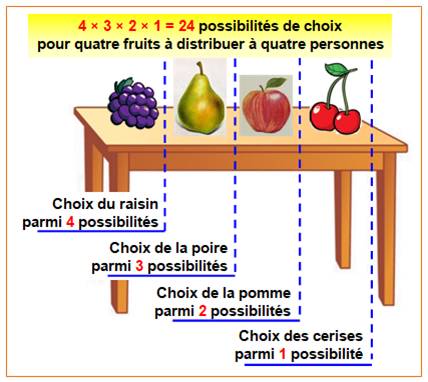
Illustration
avec choix de quatre fruits
Voir Brève
de maths - Factorielles
|
|
|
|
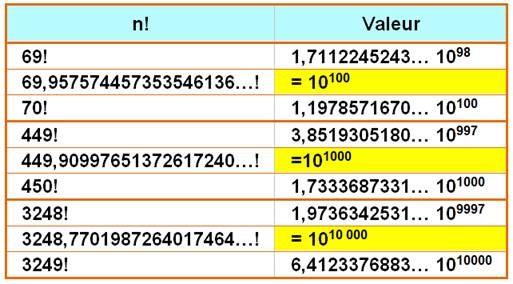
Exemples de valeurs
Valeurs
de transition en puissances 10
Explications: les factorielles sont limitées aux nombres entiers. La fonction Gamma
est la fonction des factorielles généralisées aux nombres réels.
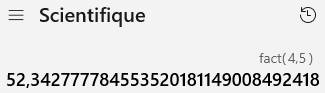
Cependant les logiciels et calculettes calculent directement les
factorielles de nombres réels. Exemple
avec calculette
Exemple
avec logiciel Maple
Merci à Denis Bertin pour cette remarque
|
|
Suite en Table des factorielles / Calcul des factorielles / Quantité de permutations des nombres
/
|
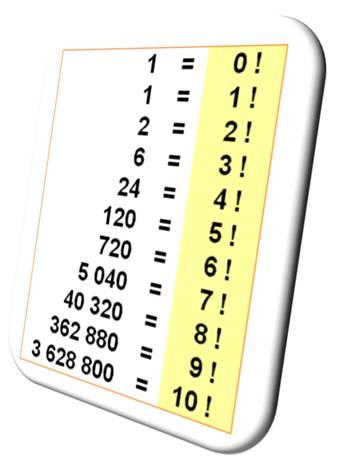
Comment
montrer logiquement que 0! = 1
Autre
méthode: (x
+ 1)! = (x + 1) x! Avec x = 0: (0+1)! = (0 + 1) 0! 1! = (1) 0! 1 = 0! |
Voir Nombre
0
|
Amusement avec
des factorielles: En effet,
soustraction de fractions: Or 100! = 99! x
100: |
|
Racine
carrée des factorielles

|
Harshad Factorielles
divisible par la somme de ses chiffres: nombres de Harshad. NON-Harshad Il
faut atteindre 432 pour trouver un nombre factoriel qui n'est pas divisible
par la somme de ses chiffres. Liste: 432, 444,
453, 458, 474, 476, 485, 489, 498, … |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette
page |
![]()