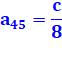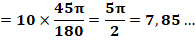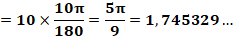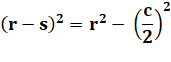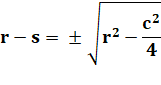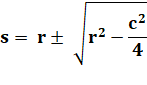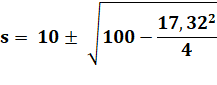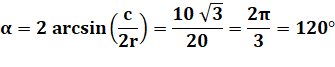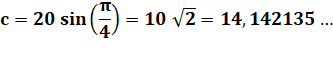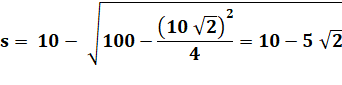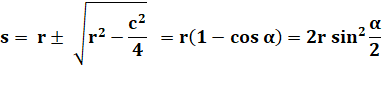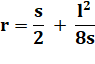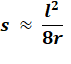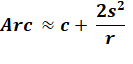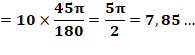|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ARCS, CORDES & SAGITTAS Définition, calcul des
longueurs et exemples.
|
Voir Formules
du cercle
Voir Angles en
radians
Voir Angles en
radians
Merci à Emmanuel B.
|
|
||
|
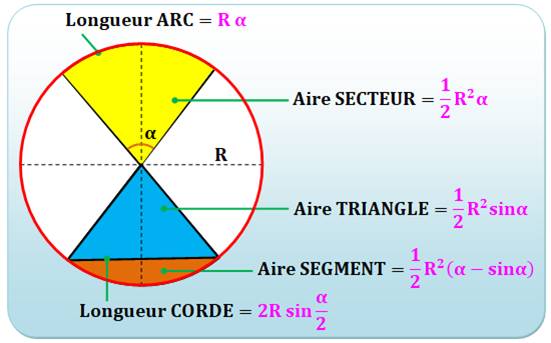
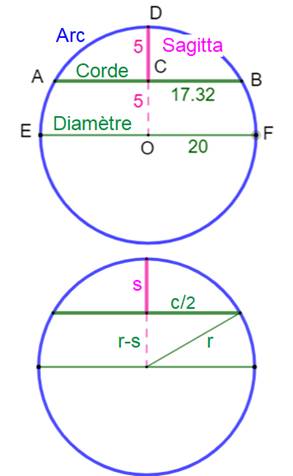
Définition La sagitta (abréviation: sag) est la
hauteur d'un arc de cercle. C'est le segment qui relie le milieu de la corde
au milieu de l'arc. C'est la flèche de
l'arc. Elle est située sur le rayon perpendiculaire à la
corde. Notion utilisée notamment en architecture et en
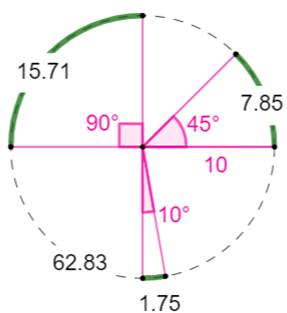
optique. Cas où la corde est connue Dans le
triangle rectangle
Exemple La distance h du centre du cercle à la corde (apothème) est égale au rayon diminué de la
sagitta. L'angle intercepté par la corde vaut: |
|
|
|
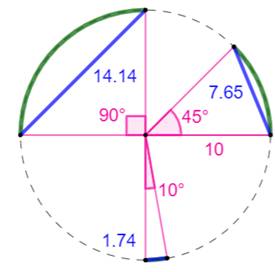
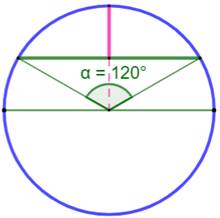
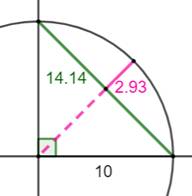
Exemple avec un angle de 90°
|
|
|
Formulaire avec sagitta (ou versin
alpha)
|
Général
Pour s petit comparé à r
|
Graphe pour c (rouge) et s (bleu) avec un cercle de
rayon unité
En radians
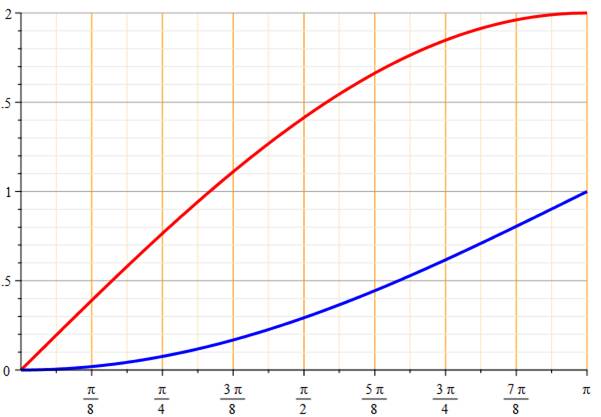
En degrés
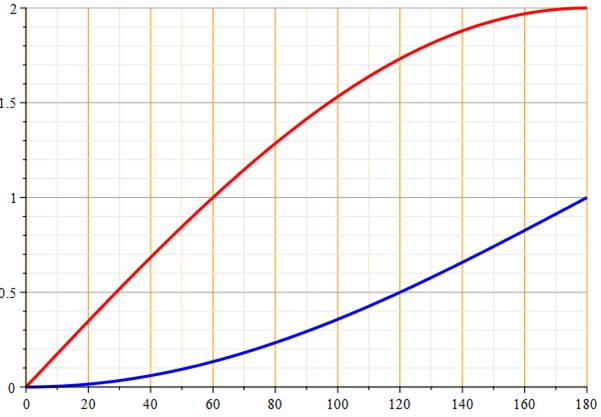
Verse sinus (anglais: versine)
|
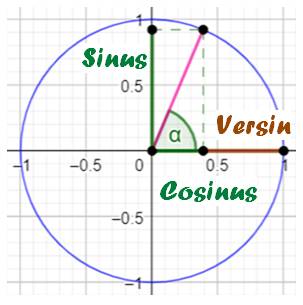
VERSE SINUS: fonction trigonométrique
(notée versin) utilisée autrefois en astronomie. Sur le cercle trigonométrique c'est le complément
du cosinus pour atteindre le rayon; c'est la flèche de l'arc ou sagitta.
Famille
ce des fonctions trigonométriques: Versin, coversin,
versosin, covercosin, haversin,hacoversin, haversosin, hacovercosin. |
Graphe sinus (rouge, cosinus (bleu) et versin (vert)
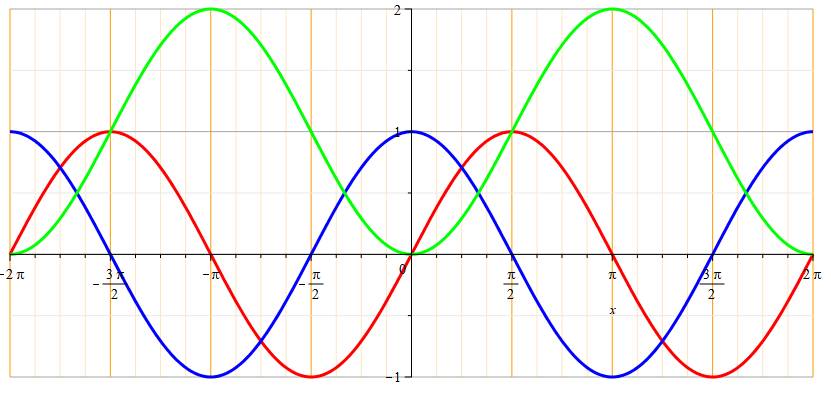
Diverses fonctions trigonométriques
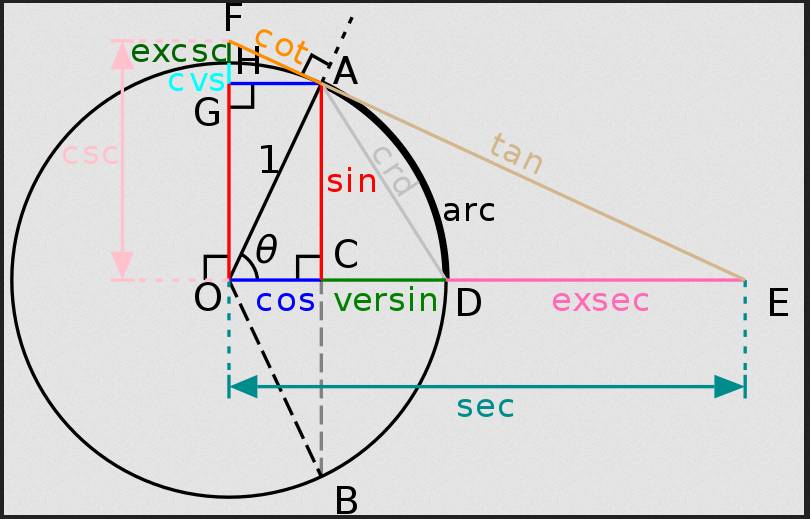
Source
Wikipédia
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()