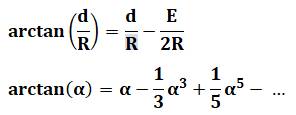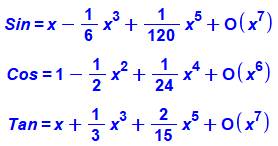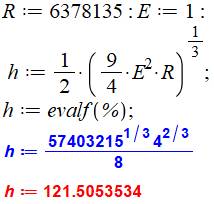|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
Corde enroulée tendue autour d'un cercle La longueur de la corde est
légèrement supérieure au périmètre. Trois
Le premier cas correspond à
un paradoxe classique, expliqué sur la page périmètre
du cercle. Le deuxième cas se déduit du
premier: la hauteur est doublée. Le troisième cas est très
inattendu du fait la hauteur atteinte. Le calcul formel est assez simple. Les
applications numériques sont plus délicates. |
Anglais: Rope aroud the earth riddle
|
Nom |
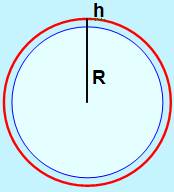
CONCENTRIQUE |
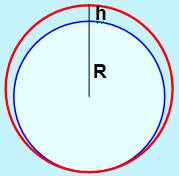
TANGENT |
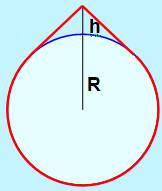
CHAPEAU de CLOWN |
|
Illustration E est l'allongement
de la corde (rouge – bleu) |
|
|
|
|
CERCLE R = 10 cm E = 7 cm |
1,12 cm |
2,25 cm |
6 cm |
|
TERRE R = 6 400 km E = 1 m |
0,16 m |
0,32 m |
121 m |
Pour h
très petit devant R
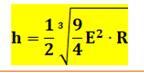
|
|
||||||
|
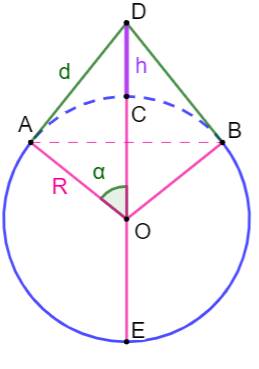
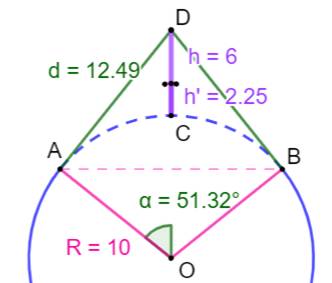
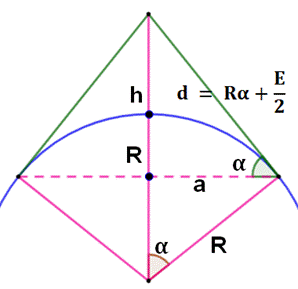
Problème Une corde est tendue autour d'un cercle. Cette corde est allongée et, elle est soulevée en
un point. Quelle est la hauteur maximale de ce point. Solution (Illustration
du haut) La corde allongée dessine le contour d'un grand
cercle jusqu'aux deux points de tangence (AEB). Elle est prolongée par les
deux segments de tangence (ADB). Différence de longueur: E = VERT – Pointillé
BLEU. C'est l'allongement de la corde.
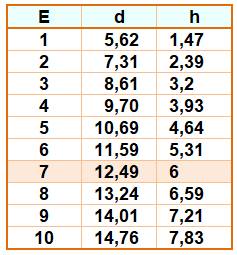
Le tableau ci-dessous présente la mise en
équation. Pas de difficulté particulière. La colonne de droite permet la
vérification de la formulation selon les valeurs indiquées sur la figure. La résolution de l'équation pour trouver
"d" a été réalisée par logiciel. |
|
|||||
|
Formulation
Résolution par logiciel (Maple)
|
||||||
|
|
||
|
Approximation de l'angle alpha Nous avons vu que l'équation à résoudre est
"compliquée". Tout tient à l'évaluation de l'angle alpha. Or, lorsque l'angle est petit, sa tangente est
proche de sa valeur en radians. Cela ne suffit pas. Un développement
en série est nécessaire. On se limitera au terme du troisième degré. |
|
|
|
Formulation
|
||
|
|
||
|
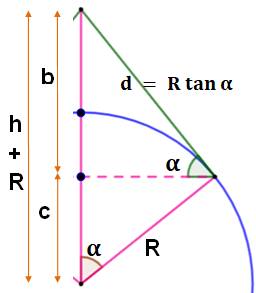
Principe Ce calcul produit une formule approchée pour la
hauteur h. Elle est un peu plus subtile que la précédente. Elle recourt aussi aux développements en série. Calcul de l'angle
Calcul de la hauteur
|
Développées
Figure pour calcul de l'angle
Figure pour calcul de la hauteur Application numérique |
|
Voir Brève
728
|
Le paradoxe
de la corde tendue est surprenant. Celui de la corde soulevée l'est
encore plus. En effet, la hauteur atteinte par la corde soulevée défie
l'intuition. Le calcul formel est délicat sans logiciel
mathématique (Maple).
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()