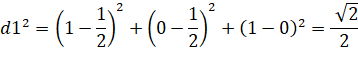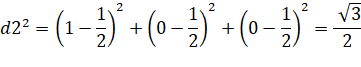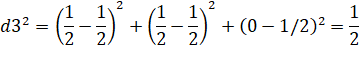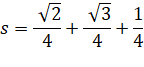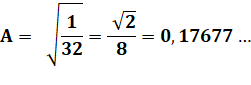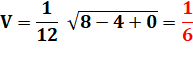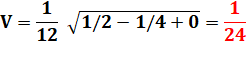|
Édition du: 08/03/2022 |
|
INDEX |
Tétraèdre |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Volume du tétraèdre Exercice
particulier, occasion de calculs sur le tétraèdre quelconque. |
||
|
|
Sommaire de cette page >>> Le tétraèdre à étudier >>> Calcul de l'aire du triangle >>> Volume du grand tétraèdre >>>
Volume du grand tétraèdre – Calcul matriciel |
Débutants Glossaire |
|
Coordonnées des sommets On connait
le tétraèdre par les coordonnées dans l'espace de ses quatre sommets. On
demande de calculer son volume. |
A (1, 0,
0) B (0, 0,
0) C (1, 1,
0) D (1, 1,
1) |
|
|
On
partage le tétraèdre initial par un triangle AJK. les points j et k sont sur
les arêtes du tétraèdre. Calculer l'aire
de ce triangle. Calculer
le volume du petit tétraèdre dégagé au sommet. |
A (1, 0,
0) J (1/2,
1/2, 1/2) K (1/2,
1/2, 0) |
|
|
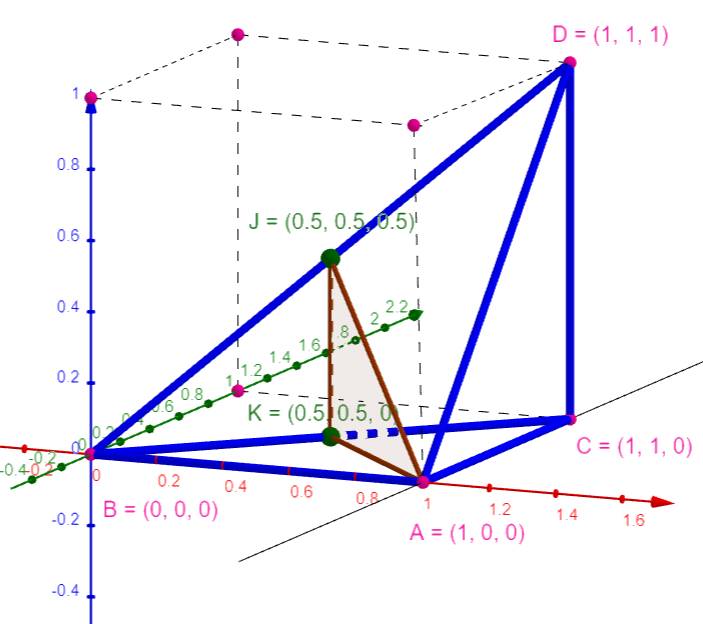
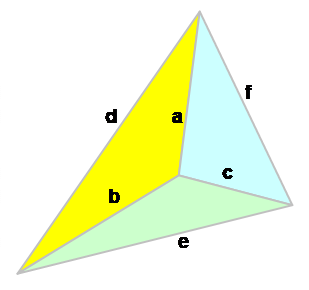
Représentation Dessin avec le logiciel GeoGebra 3D. Système de coordonnées à trois axes et
positionnement des points A, B, C, D, J et K. Le tétraèdre est en bleu. Le triangle de partage
est en marron.
|
|
Longueur
des côtés du triangle |
|
|
|
Demi-périmètre |
|
|
|
et tous
calculs faits: |
|
|
|
|
|
|
|
|
Grand tétraèdre |
Petit tétraèdre |
|
Côtés |
a = b = 1 c = 1 d = e = f = 1 |
a = 1/2 b = c = d = 1/2 e = 1 f = |
|
Calculs |
D = a² + b² – d² = 2 + 1 – 3 = 0 E = b² + c² – e² = 1 + 1 – 2 = 0 F = a² + c² – f² =
2 + 1 – 1 = 2 |
D = 1/4 + 1/2 – 1/4 = 1 E = 1/2 + 1/2 – 1 = 0 F = 1/4 + 1/2 – 3/4 = 0 |
|
|
P = 4 a² b² c² = 8 Q = a² E² + b² F² + c² D² =
0 + 4 + 0 = 4 R = D E F = 0 |
Q = 1/4 P = 0 + 0 + 1/2 R = 0 La somme sous le radical doit être positive |
|
|
|
|
|
Rapport |
1 |
1/4 |
|
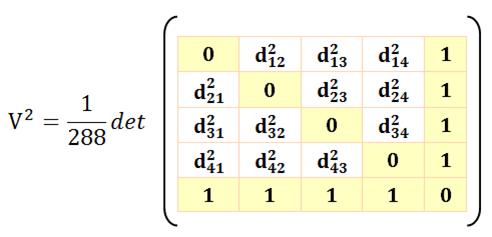
Calcul matriciel |
|||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
Calcul réalisé avec le logiciel Maple Le déterminant vaut 8. |
|
||||||||||||||||||||||||||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |