|
|||||||||||||||||||||||||||||||||||||
![]()
Humour
|
Un octogone a huit côtés et un décagone en a dix; et un Carlos Ghosn ? Il en a des millions de côté, des euros … Carlos Ghons:
né en 1954, PDG de Renault-Nissan de 2005 à 2019 |
Voir Pensées et Humour
|
Ligne
brisée fermée; ligne polygonale. Polygone Figure plane formée par une ligne polygonale (S1
, S2 … Sn ) telle que l'extrémité de S1
non commune à S2 soit confondue avec l'extrémité de Sn
non commune à Sn-1 Côtés du polygone Les segments S1 S2 , S2
S3 … s'appellent les côtés
du polygone et leurs extrémités les sommets. Un segment joignant deux sommets non-consécutifs est
une diagonale. Ordre du polygone Le nombre de ses côtés. Un polygone d'ordre cinq (pentagone) possède cinq sommets, cinq angles et cinq
côtés. |
Polygones réguliers
|
Triangle équilatéral / Carré / Pentagone /
Hexagone / Heptagone / Octogone / Décagone / Dodécagone
Polygones étoilés |
Voir Nom des polygones
Arithmétique des polygones – Énigme
|
Résoudre Triangle² =
Pentagone + Carré. Carré² =
Hexagone + Hexagone Carré. Pentagone² =
Hexagone + Hexagone + Hexagone + Carré + Triangle. Hexagone² = Octogone
+ Octogone + Octogone + Octogone + Carré. |
Solution 3 => 3² = 5 + 4 4 => 4² = 6 + 6 + 4 5 => 5² = 6 + 6 + 6 + 4 + 3 6 => 6² = 8 + 8 + 8 + 8 + 4 |
|
|
Résoudre
|
Au moins, trois
solutions 1)
Il s'agit
du carré du nombre de côtés. 2)
Il s'agit
de la quantité de sommets. 3)
Il s'agit du
périmètre au carré. |
|
Voir Nombres
polygonaux / Énigmes
virales
![]()
|
|
|||
|
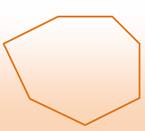
Convexe Convex |
|
Toutes les diagonales sont internes au
polygone. |
|
|
Croisé Crossed |
|
Son enveloppe est la ligne brisée qui forme le
contour. |
|
|
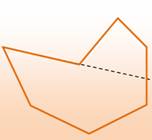
Concave Concave |
|
Il existe au moins une diagonale non
complètement incluse dans le polygone. |
|
|
Équilatéral Equilateral |
|
|
|
Équiangle Equiangle |
|
|
|
Régulier Regular |
|
Et équiangle A regular polygon is a polygon
that is both equilateral (all sides are congruent) and
equiangular (all angles are congruent).
|
|
Irrégulier |
|
|
|
Irrégulier inscrit Inscribed irrégular |
|
|
|
Irrégulier non-inscrit Non-inscribed irrégular |
|
|
|
Étoilé Star |
|
|
Les
premiers polygones réguliers étoilés
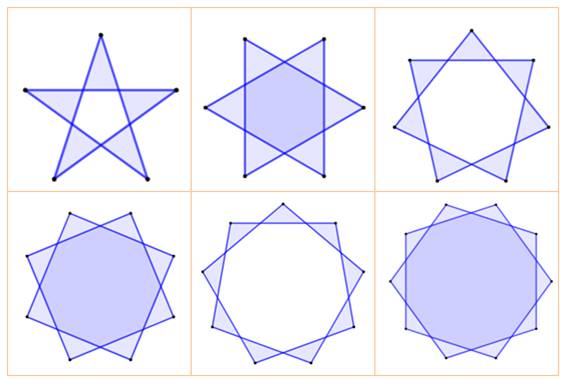
![]()
Accès par
la quantité de côtés
|
1.
De tous les polygones à n côtés, c'est le
polygone régulier à n côtés qui offre le maximum
de surface. 2.
De tous les polygones à n côtés ayant une
aire donnée, c'est le polygone régulier à n côtés qui offre le périmètre minimum. 3.
L'aire A et le périmètre P d'un polygone
à n côtés satisfont l'inégalité (l'égalité étant établie pour un polygone
régulier à n-côtés):
|
|
|
||
|
|
||
|
monogone,
hénagone (n'existe pas, du domaine du segment) |
||
|
2 |
digone
(angle) (polygone dégénéré) |
|
|
3 |
trigone
(triangle), trilatère |
|
|
4 |
tétragone
(quadrilatère) |
|
|
5 |
||
|
6 |
||
|
7 |
||
|
8 |
octogone |
|
|
9 |
ennéagone, nonagone |
|
|
hendécagone
ou un décagone |
||
|
12 |
||
|
13 |
triskaidécagone
("kai" signifie "plus"), tridécagone |
|
|
14 |
tétrakaidécagone,
tétradécagone, quadridécagone |
|
|
15 |
pentakaidécagone,
pentadécagone, quidécagone |
|
|
16 |
hexakaidécagone,
hexadécagone |
|
|
17 |
heptakaidécagone,
heptadécagone |
|
|
18 |
octakaidécagone,
octadédagone |
|
|
19 |
ennéakaidécagone,
ennéadécagone |
|
|
icosagone |
||
|
21 |
icosikaihenagone,
icosihenagone |
|
|
22 |
icosikaidigone |
|
|
icosikaitrigone |
||
|
24 |
icosikaitétragone |
|
|
25 |
icosikaipentagone |
|
|
26 |
icosikaihexagone |
|
|
27 |
icosikaiheptagone |
|
|
28 |
icosikaioctagone |
|
|
29 |
icosikaiennéagone |
|
|
30 |
triacontagone
("conta" = "dizaine") |
|
|
31 |
triacontakaihenagone |
|
|
40 |
tétracontagone |
|
|
pentacontagone |
||
|
60 |
hexacontagone |
|
|
70 |
heptacontagone |
|
|
80 |
octacontagone |
|
|
90 |
ennéacontagone |
|
|
hectogone,
hecatontagone |
||
|
chiliogone
ou chiliagone |
||
|
myriagone |
||
|
Et en anglais? For example, a 100-sided
polygon is called a hectagon, centagon or 100-gon. In general, any n-sided
polygon with over 12 sides is called an
n-gon. While there are other conventions for naming polygons with any number
of sides, it is most common to use the n-gon form. |
||
Voir Nombres en grec / Nom des grands nombres / Tables de nombres / Alcanes /
Nom des bases de numération
|
|
|
|
|
|
Voir Calcul
de Pi
Théorème de Viviani
|
Pour
tout polygone régulier, la somme des distances d'un point intérieur
quelconque aux côtés est égale à la longueur de la hauteur. >>> |
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Polygone.htm |
![]()