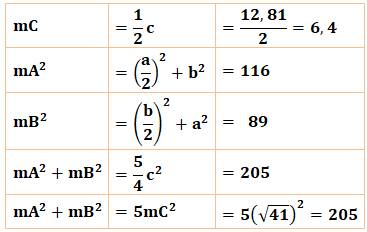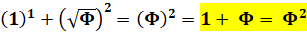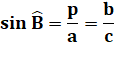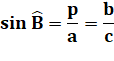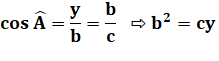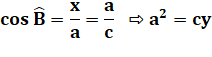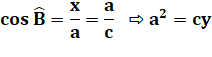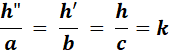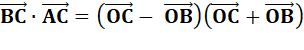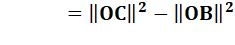NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 09/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Types de TRIANGLES				Glossaire Triangle
INDEX Triangle rectangle Triangle Géométrie	Types	Rectangle	Isocèle	Équilatéral
	Quelconque	Obtusangle	Sphérique	Calabi
	Isométriques	Semblables	Homologique	Particuliers
	Triangles rectangles	Rectangle	Isiaque	Propriétés diverses
		Congruents	de Pythagore	Constructions
		Sommaire de cette page >>> Propriétés du triangle rectangle >>> Médianes dans le triangle rectangle >>> Le plus célèbre: le triangle 3456 >>> Triangles rectangles entiers >>> Triangle c = 2b >>> Triangles rectangles typiques >>> Triangle doré de Kepler >>> RELATIONS MÉTRIQUES >>> Triangle rectangle & rectangle >>> Triangle rectangle & cercle >>> Triangle rectangle & cône >>> Hypoténuse et côté plus un >>> Trigonométrie >>> Périmètres identiques >>> Aire en nombres entiers >>> Triangle rectangle – Index

Perle mathématique (vu sur copie du bac): le triangle rectangle est un triangle qui a trois côtés parallèles.

Voir Pensées & humour

TRIANGLE RECTANGLE

Célèbre triangle ! Si simple et si étudié.

Ceinturé par l'extraordinaire théorème de Pythagore, et

Mesuré sous toutes les coutures par la trigonométrie.

Le grand côté est l'hypoténuse. Les deux autres sont les cathètes.

Un triangle rectangle qui a deux côtés égaux est un triangle rectangle isocèle, sinon c'est un triangle rectangle scalène.

Un rectangle coupé en deux par une de ses diagonales forme deux triangles rectangles.

Tout triangle partagé par une de ses hauteurs donne naissance à deux triangles rectangles.

Anglais: Right triangle, right-angled triangle;

The side opposite the right angle is called the hypotenuse

Devinette

Le Dab de Paul Pogba est-il parfait? Claire, une prof de maths à Aubervilliers, en a fait un problème divertissant de mathématiques (nov. 2016) pour ses élèves de 4^ème.

La question revient à demander si les deux triangles sont rectangles.

Paul Pogba, né en 1993 en Seine-et-Marne, est un joueur de football.

Solution

Propriétés du triangle rectangle
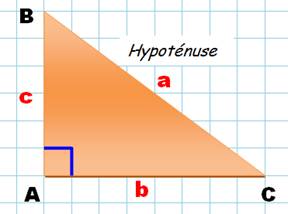
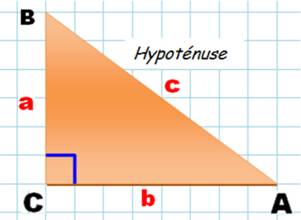
Le triangle rectangle possède un angle droit (A). Cet angle est signalé par la petite équerre bleue) Le côté opposé (BC) à l'angle droit se nomme l'hypoténuse. Les deux autres côtés (AB et AC), adjacents à l'angle droit, sont les cathètes. Selon l'angle considéré (B ou C), les cathètes deviendront sinus pour l'une et cosinus pour l'autre; c'est la base de la trigonométrie.	A < 90° Triangle acutangle A = 90° Triangle rectangle A > 90° Triangle obtusangle
Le triangle rectangle est inscrit dans un demi-cercle. L'hypoténuse est son diamètre. Voir Bissectrice de don angle droit
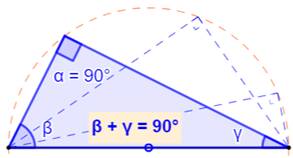
Ses trois angles A, B et C. Les angles B et C sont complémentaires. Si B = C = 45°, le triangle est rectangle-isocèle.	A + B + C = 180° A = 90° B + C = 90° B 45° C 45°
Ses trois côtés a, b, c: (Théorème de Pythagore)	a < b + c a² = b² + c² Voir Relations métriques
Périmètre Aire	P = a + b + c A = ½ c . b
Relations trigonométriques Voir Relations dans le triangle quelconque
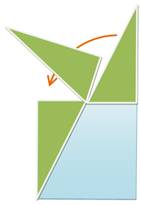
Le triangle rectangle est un demi-rectangle coupé par une de ses diagonales. Tout triangle peut être partagé en deux triangles rectangles de trois façons en dessinant les hauteurs. C'est la base du calcul de son aire. La trigonométrie s'applique au triangle rectangle. L'hypoténuse est l'un des diamètres du cercle circonscrit. Sa longueur est double de celle de la médiane issue de l'angle droit. Voir ci-dessous.

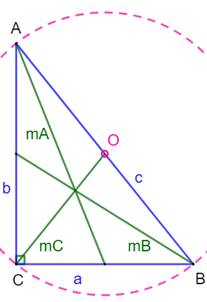
Médianes dans le triangle rectangle

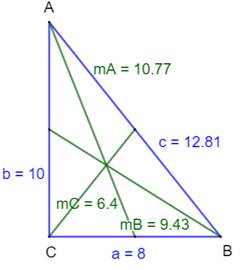
Formules Hypoténuse AB = c = diamètre du cercle circonscrit = 2R Application numérique

Médianes mA, mB et mC Exemple

Le plus célèbre! – Le triangle 3456
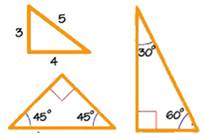
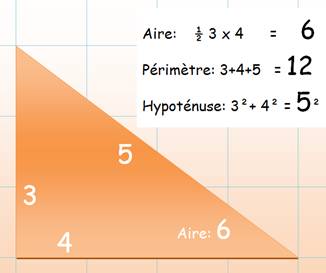
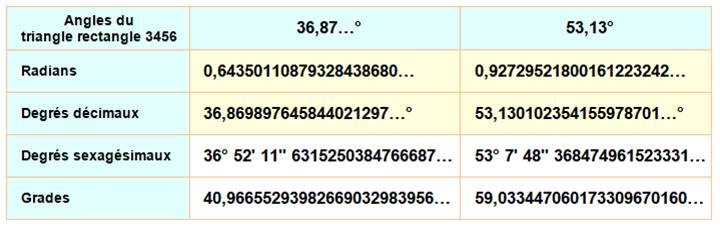
Un triangle rectangle qui arrive à faire une suite de nombres: 3, 4, 5, 6. Un triangle dont l'hypoténuse et l'aire sont des entiers, dit aussi triangle isiaque. Note: un triangle dont les mesures des côtés et de l'aire sont entières ou rationnelles est dit héronien. Les deux angles: 36,87…° et 53,13…° >>>	Diamètre du cercle inscrit : 2
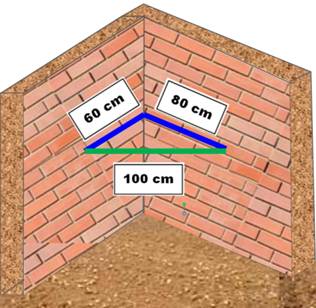
En adoptant un coefficient 20 (rapport d'homothétie), ce triangle devient celui des maçons ou, plus généralement, des arpenteurs. Avec 60 cm et 80 cm marqués sur les murs, ils contrôlent que la distance entre les extrémités est bien de 1 m. Voir Corde du jardinier

Voir Triangles rectangles héroniens et nombres congruents / Triangle 345 en équation / Énigme du carré dans ce triangle /

Humour avec ce triangle / Origine du préfixe penta et ce triangle

Valeurs précises des angles

Voir Angles et leurs notations

Triangles rectangles entiers (Pythagoriens)
Nous venons de voir le cas (3, 4, 5). Cas général Pour tout nombre entier a > 3, il existe toujours un triangle dont les longueurs des côtés sont des nombres entiers (triplets de Pythagore). Formules Si a = 2n, le triangle est: {2n, n² – 1, n² + 1} Si a = 2n + 1, le triangle est: {2n + 1, 2n(n + 1), 2n(n + 1) + 1}		Exemple {6, 8, 10} c² = a² + b² = 6² + 8² = 64 + 36 = 100 = 10²
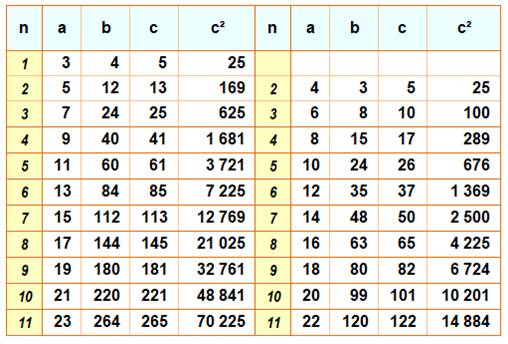
Valeurs des côtés Pour a allant de 3 à 23. Nombres impairs à gauche et pairs à droite. Et valeur correspondante de n en colonne jaune.	Tableau Exemples de lecture a = 10; alors n = 5 et b = 5² – 1 = 24 et c = 5² + 1 = 26. a = 11; alors n = 5 et b = 2x5x6 = 60 et c = 2x5x6 + 1 = 61. Commentaires Lorsque que a est impair les valeurs de b et c sont consécutives. Lorsque a est pair, ces valeurs sont écartées de deux unités.

Merci à Luc et à Michel pour leurs idées d'améliorations

TRIANGLE c = 2b
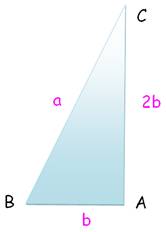
Ce triangle rectangle a la même aire qu'un carré de côté mesurant b. Aire = ½ b x 2b = b² Ce type de rectangle est à la base d'une énigme de découpage du carré en cinq parties égales. Avec Pythagore: a² = b² + (2b)² = 5b² a = b5 Voir Racine de 5 Angle en C: = Artg(1/2) = 26,5650 …°

Voir Rectangle d'or

Triangles rectangles typiques
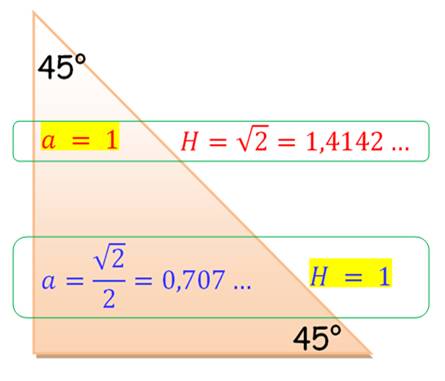
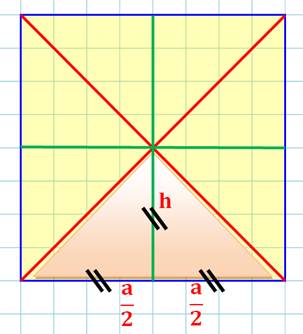
Triangle rectangle isocèle 45-45 (demi-carré) Dimensions selon que le côté a mesure 1 ou l'hypoténuse H mesure 1. En effet, théorème de Pythagore: H² = a² + a² H = a Hauteurs du triangle rectangle-isocèle Une des hauteurs du triangle rectangle-isocèle est égale à la demi-base. Les deux autres sont confondues avec les côtés.

Voir Triangle rectangle isocèle rationnel / Aire du carré et des couronnes

Triangle rectangle 30-60

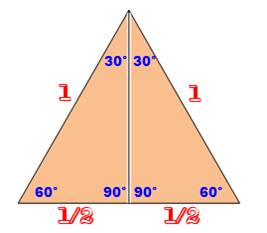
(triangle hémi-équilatéral ou triangle de l'écolier)

Première propriété: la longueur du plus long côté (hypoténuse) est le double de celle du plus petit côté. Pour s'en persuader, il suffit de coller deux de ces triangles côte à côte et de former un triangle équilatéral.

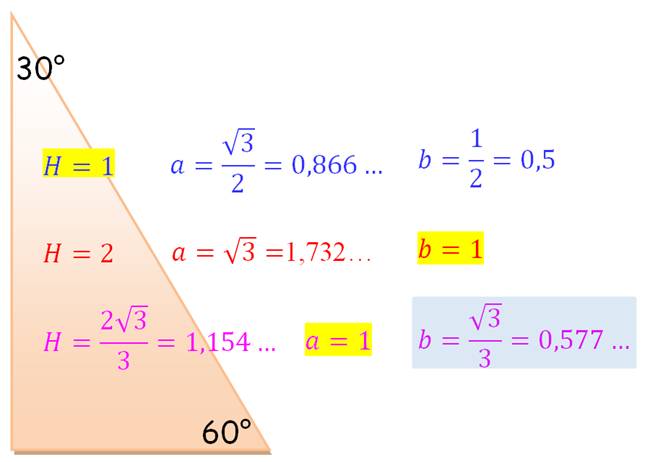
Dimensions selon que l'hypoténuse H mesure 1, ou les côtés a ou b.

Deux tels triangles accolés par le grand côté donne un triangle équilatéral.

L'hexagone est formé de 16 tels triangles.

Voir Sangaku aux cinq cercles / Énigme du carré et quatre demi-cercles

Triangle rectangle 20-70 (ou presque: 20,01-69,99)

Triangle qui est impliqué dans la construction d'un ennéagone presque parfait.

Triangle rectangle a-b

Table de ce type de triangles rectangles

Triangle rectangle d'or 18-72

Deux tels triangles accolés par le grand côté forment un triangle isocèle d'or, lequel constitue chacune des cinq branches de l'étoile à cinq branches.

Il existe deux autres triangles rectangles à section dorée.

Triangle doré de Pythagore

Triangle rectangle dont le nombre d'or est l'hypoténuse >>>

Triangle isiaque et voisins

Triangle rectangle sacré ou isiaque ou 345 … >>>

Triangle (1 , 2 , )

Base de la construction du losange doré >>>

Triangle Sangaku

Deux côté sont somme et différence de deux longueurs >>>

Voir Triangles rectangles et leur hypoténuse

Triangle de Kepler

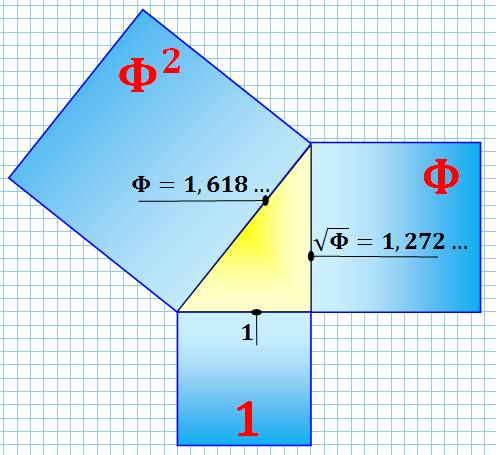
Triangle rectangle dont les longueurs des côtés sont en progression géométrique de raison dorée. Basé sur la relation du nombre d'or qui épouse le théorème de Pythagore:

Curiosité

Périmètre du cercle circonscrit au triangle:
Périmètre du carré de droite:
Écart:	0,0048… soit 0,095%

Voir Kepler – Biographie / Brève 691

RELATIONS MÉTRIQUES

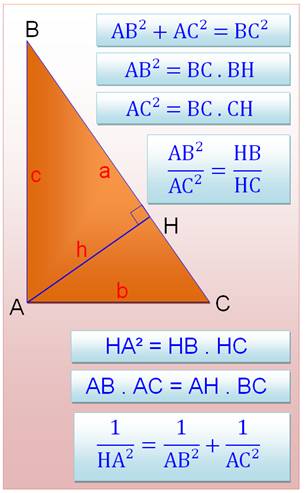
Principales relations dans le triangle rectangle:

	a, b, c	h
Hauteur	h = b.c / a	h² = HB.HC
Côtés	a² = b² + c²
Aire	A = ½ b.c	A = ½ a.h

Voir SUITE / Moyenne géométrique
/ Théorème de Pythagore

Voir RAYON du cercle inscrit

Voir Calcul de l'aire de l'arbelos / Quadrature du triangle / Brève 667

Démonstration de l'inverse du théorème de Pythagore

Démonstrations pour quelques relations		haut
ab = pc Avec expression de l'aire de deux manières: 1/2 ab = 1/2 pc Avec le sinus de B exprimé de deux manières: Voir autre Illustration
a² + b² = c² Démonstration du théorème de Pythagore), avec expression des cosinus des angles: a² + b² = cx + cy = c (x + y) = c²	1/p² = 1/a² + 1/b² En reprenant la première relation: ab = pc p = ab / c En utilisant le théorème de Pythagore:

Exemple de calcul
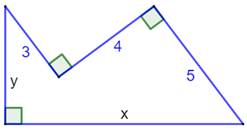
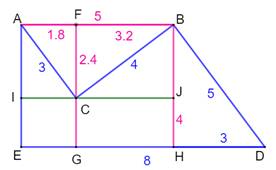
Problème Soit cette forme avec trois angles droits. Est-il possible de déterminer les longueurs x et y ? Solution (figure du bas)

Voir Triangles fsemblables

Triangle RECTANGLE et sa HAUTEUR

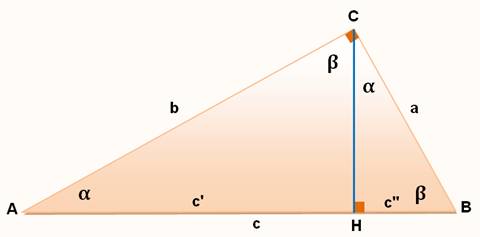
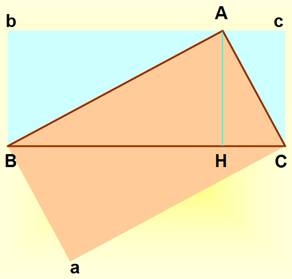
Angles égaux et complémentaires La somme des angles d'un triangle est 180° Dans un triangle rectangle, avec un angle droit, la somme des deux autres angles est 90°. Ils sont complémentaires. C'est le cas pour les angles et notés sur la figure. Triangles semblables: Thales et Pythagore Les trois triangles de la figure: ABC, CBH et ACH ont des angles égaux ( et et un angle droit), ils sont semblables (ou homothétiques). Nous pouvons emboiter ces trois triangles comme indiqué sur la figure. Le théorème de Thales s'applique à ces trois triangles. 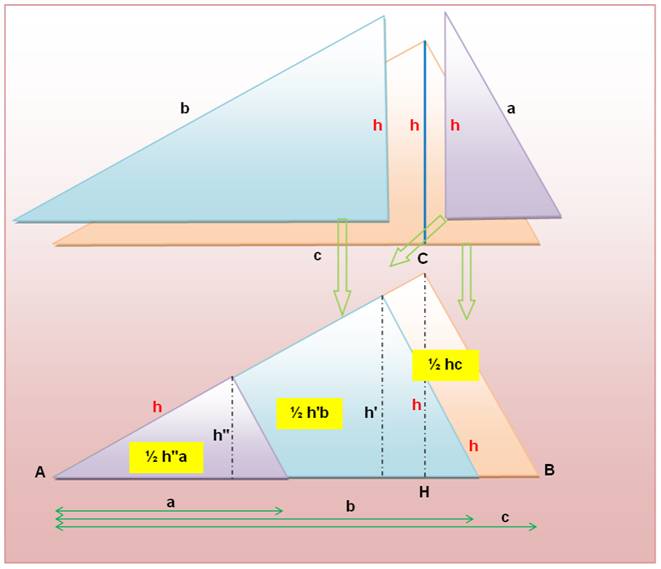Outre le rapport des longueurs des côtés, celui des hauteurs à la base est constant: De part notre construction (figure du haut), l'aire du grand triangle est égale à la somme des deux plus petits: ½ h.c = ½ a.h" + ½ b.h' h.c = a.h" + b.h' Remplaçons les h par leur valeur donnée ci-dessus en fonction de k, le rapport d'homothétie: k.c.c = k.a.a + k.b.b c² = a² + b² Soit, une démonstration originale du théorème de Pythagore.

TRIANGLE rectangle & RECTANGLE

Plus facile avec deux rectangles !

AB . AC = BC . AH

Démonstration

Aire du rectangle ocre	AB . AC
et aussi, 2 fois celle du triangle ABC	2 x AT
Aire du rectangle bleu	BC . AH
et aussi, 2 fois celle du triangle ABC	2 x AT
En constatant l'égalité	AB . AC = BC . AH

Voir Démonstrations de quelques relations

TRIANGLE RECTANGLE et CERCLE
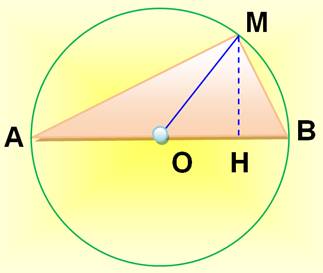
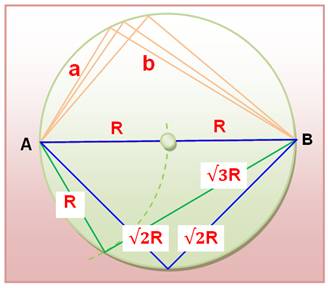
Tous les triangles inscrits dans le cercle et dont un côté est le diamètre (comme AMB) sont rectangles. Dans un triangle rectangle, le milieu de l'hypoténuse est le centre du cercle circonscrit à ce triangle. OM est l'une des médianes du triangle rectangle ABM. Elle découpe le triangle rectangle en deux triangles – AOM et MOB – qui ont même aire. Base égale (AO = OB) et même hauteur (MH); L'angle MOB est le double de l'angle MAB. Tous les triangles de cette figure sont rectangles. Avec le théorème de Pythagore: a² + b² = 4R² si a = b => a = R si a = R => b = R

Voir Cercle inscrit

Démonstration avec somme de vecteurs		haut
Vecteurs bleus Produit scalaire Les normes des vecteurs OC et OB (leur longueur) sont égales.	AB est un diamètre et C est un point sur le cercle, alors l'angle en C est droit.

TRIANGLE RECTANGLE et CÔNE
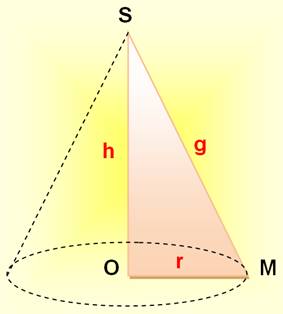
Un triangle rectangle en rotation autour d'un de ses côté engendre un cône. Le disque (directrice du cône) de centre O et de rayon r est la base du cône. La surface engendrée par l'hypoténuse du triangle rectangle, la génératrice g du cône, engendre la surface latérale du cône. Le point S est le sommet du cône. Le segment OS est la hauteur du cône.	Suite en Cône

Hypoténuse égal côté + 1

Trouver les triangles rectangles

dont la longueur de l'hypoténuse est égale à celle d'un côté plus 1.

H² =	A² + B²
(A+1)² =	A² + B²	Exemple:
2A + 1 =	B²	B = 9	A = (81-1)/2 = 40
A =	(B² - 1) / 2		H = 41

B	A	H
1	0	1
2	1,5	2,5
3	4	5
4	7,5	8,5
5	12	13
6	17,5	18,5
7	24	25
8	31,5	32,5
9	40	41
10	49,5	50,5

Le seul triangle dont les trois mesures sont consécutives est le triangle 3, 4 et 5.

Voir Triangles Pythagoriciens

Trigonométrie
On rappelle que la trigonométrie s'applique exclusivement aux triangles rectangles. Il faut donc, en premier lieu, montrer que le triangle est rectangle. Soit, c'est une donnée de l'énoncé; Soit, il faut le démontrer: par égalité avec un autre angle, le triangle est inscrit dans un cercle et l'un des côtés passe par son centre, on identifie un carré, etc.

Voir Exemples de relations trigonométriques

Périmètres identiques

Trois triangles rectangles, même périmètre: 120

30 - 40 - 50

24 - 45 - 51

20 - 48 - 52

Six triangles rectangles, même périmètre: 720

180 - 240 - 300	120 - 288 - 312	144 - 270 - 306
72 - 320 - 328	45 - 336 - 339	80 - 315 - 325

Voir Triangles de périmètre 20 / Côtés en progression arithmétique

Aire en nombres entiers
On cherche les triangles rectangles ayant pour côtés des fractions d'entiers, et dont l'aire est un entier. Cet entier est un nombre congruent. Les premiers nombres congruents sont 5, 6, 7, 13, 14, 15, 20, 21, 22, 23 …

Voir Triangle (13, 14, 15) / Périmètre = aire / Côtés en progression arithmétique

Devinette – Solution

Est-ce que les deux triangles sont rectangles?

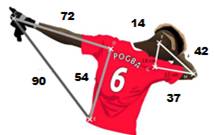
Solution classique

Avec le théorème de Pythagore, on calcule:

72² + 54² = 8 100 et 90² = 8 100 => Rectangle

14² + 37² = 1 565 et 42² = 1 764 => NON

Solution minimaliste (calcul de tête sur les unités seulement)

2² + 4² = 4 + 16 => 0 et 0² = 0 => Potentiellement rectangle.

4² + 7² = 16 + 49 => 5 et 2² = 4 => Incompatible; non rectangle.

Solution avec théorie des nombres (petit triangle)

Propriété des triplets de Pythagore: dans un triplet primitif, le nombre le plus grand est impair. Le triplet {14, 37, 42} est primitif (aucun facteur commun), or le nombre le plus grand est pair. Ce n'est pas un triplet de Pythagore.

Plus simplement: pair² + impair² = impair, incompatible avec pair² = pair.

Retour / Voir Proportions du corps humain / Autres problèmes à la mode sur le Net

Triangle rectangle	Triangle rectangle – Suite (propriétés diverses) Triangle rectangle – Aire minimale Triangle rectangle – Avec lunule Triangle rectangle – Bissectrice, hauteur et médiane Triangle rectangle – Carrés inscrits Triangle rectangle – Cercle inscrit Triangle rectangle – Constructions élémentaires Triangle rectangle – Conway Triangle rectangle – Doubler Triangle rectangle – Exercices de quatrième Triangle rectangle – Isiaque (3, 4, 5) Triangle rectangle – Progression arithmétique Triangle rectangle – Propriétés diverses, énigmes Triangle rectangle – Quadrupler Triangle rectangle – Résolution, cas classiques Triangle rectangle – Résolution, cas spéciaux Triangle rectangle – Résolution avec aire et périmètre Triangle rectangle – Théorème de Pythagore Triangle rectangle – Type 345 en équation Triangles dans le Stomachion (puzzle d'Archimède) Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles Allumettes Angle Carrés Cercles DicoMot	Droite Égalités des triangles Géométrie – Index Jeux – Index Polygones Probabilité d'obtenir un triangle obtusangle Quadrupler le triangle Résolution du triangle quelconque Symétries
DicoNombre	Nombre Racine de 5
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TriaRect.htm