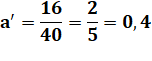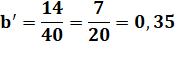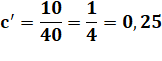|
Édition du: 20/06/2021 |
|
INDEX |
TRIANGLES Éléments remarquables |
||||
|
Éléments remarquables – Index |
|||||
![]()
|
Systèmes de coordonnées
barycentriques (scb) Barycentric coordinates Triplets
de nombres qui permettent de situer un point dans le triangle quelconque.
Focalisation sur le centre
de gravité. |
||
|
|
Sommaire de cette page >>> Coordonnées barycentriques >>> Triangle équilatéral et triangle rectangle >>> Points remarquables |
Débutants Glossaire |
|
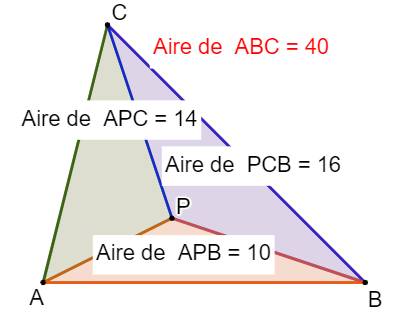
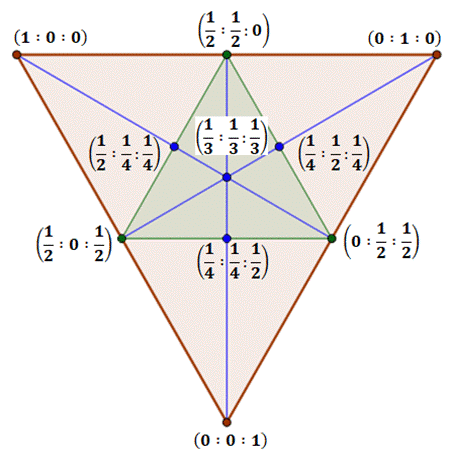
Approche Les coordonnées barycentriques
du point P par rapport au triangle ABC:
Il s'agit du rapport de l'aire des triangles
élémentaires avec l'aire du triangle complet. Propriété On note que selon le calcul: 0,4 + 0,35 + 0,25 = 1 Donc, il suffit de calculer deux coordonnées pour
connaitre la troisième. Par exemple: Avec la somme 1, on parle se systèmes de
coordonnées barycentriques normalisées |
|
|
|
Avec le déterminant |
Les |
|
|
Triangle
équilatéral
|
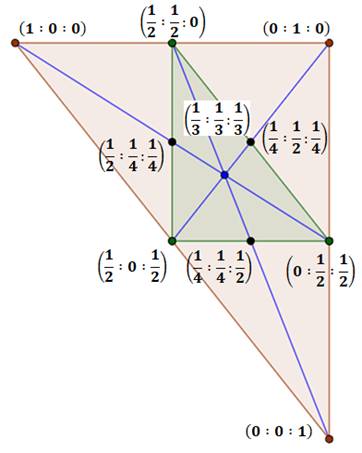
Triangle
rectangle |
|
|
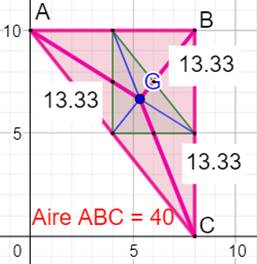
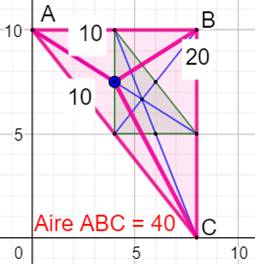
Deux exemples de
calcul des coordonnées barycentriques
|
||
|
Point |
Coordonnées barycentriques |
|
A |
(1, 0, 0) |
|
B |
(0, 1, 0) |
|
C |
(0, 0, 1) |
|
Milieu de BC |
(0, 1, 1) |
|
Milieu de CA |
(1, 0, 1) |
|
Milieu de AB |
(1, 1, 0) |
|
Centre de gravité G |
(1, 1, 1) ou
(1/3, 1/3, 1/3) en coordonnées normalisées |
|
Centre du cercle inscrit I |
(a, b, c)
|
|
Centre du cercle circonscrit O |
(a²(b²+c²–a²), b²(c²+a²–b²), c²(a²+b²–c²)) |
|
Orthocentre H |
|
|
Centre du cercle d'Euler |
|
|
Point symédian |
(a², b², c²) |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Remarqua/Barycent.htm
|