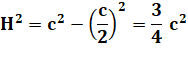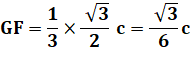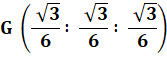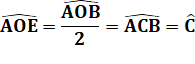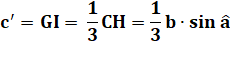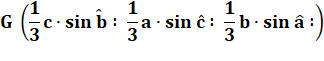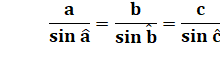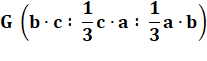|
Édition du: 03/07/2023 |
|
INDEX |
TRIANGLES Éléments remarquables |
||||
|
Éléments remarquables – Index |
|||||
![]()
|
Système de coordonnées trilinéaires
(sct) Trilinear coordinates Triplets
de nombres qui permettent de situer un point dans le triangle quelconque.
Focalisation sur le centre du cercle inscrit. |
||
|
|
Sommaire de cette page >>> Coordonnées trilinéaires >>> Distance algébrique aux côtés |
Débutants Glossaire |
|
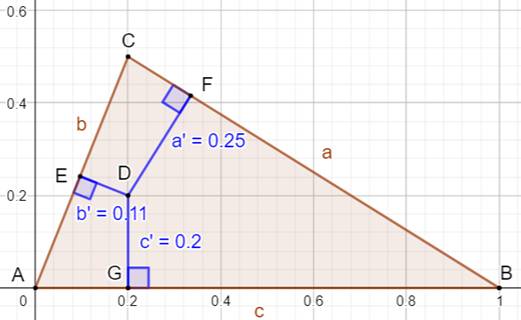
Approche Le point D dans le triangle ABC a pour
coordonnées trilinéaires:
Ce sont les distances du point aux droites
portant les côtés. Ce sont les perpendiculaires au côté à partir du point Ou
encore, les projections orthogonales du
point sur les côtés. Intérêt: Caractériser
les points remarquables du triangle par ce
simple triplet. |
Distances algébriques du point par
rapport aux côtés
|
|
|
Exemple - Coordonnées trilinéaires des sommets
|
Les coordonnées sont normalisées avec ces mesures
unités pour les sommets. Comme pour les fractions, il est possible de
diviser les trois valeurs par un facteur commun. Des triangles semblables produisent les mêmes
coordonnées trilinéaires. Le signe de chaque coordonnée indique de quel
côté se trouve le point par rapport au côté: positif du côté de l'intérieur
et négatif de l'autre côté. |
|
|
Distance par rapport à AB, côté du
triangle:
Coordonnées d'un point Trois valeurs de distance algébrique, chacune par
rapport à un côté. |
Distances positives ou négatives
|
|
|
Exemple avec le triangle
équilatéral et point G centre du cercle circonscrit Les coordonnées trilinéaires de G sont du type: Hauteur du triangle isocèle: Distance du point G par rapport à AB, valeur
positive: Coordonnées trilinéaires de ce centre G: |
Cas du triangle équilatéral et son
centre G
|
|
CT
= Coordonnées Trilinéaires
|
CT du centre
du cercle circonscrit |
||||||||||||||||
|
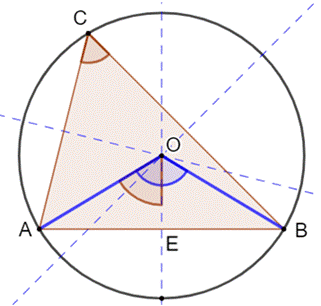
Construction Le point O est le centre du cercle circonscrit du
triangle quelconque ABC. En pointillés verts, les médiatrices qui ont servi à
la construction du point O. Rappel: l'angle
bleu au
centre vaut deux fois l'angle marron en C => Angle ACB = angle AOE.
|
Triangle ABC et son cercle
circonscrit
Coordonnées trilinéaires du centre
O
|
|||||||||||||||
|
CT de
l'orthocentre |
||
|
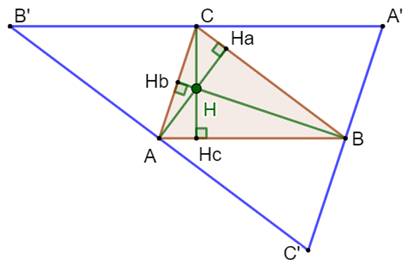
Construction de la figure On reprend la figure
qui permet de démontrer que les hauteurs se coupent en un unique point:
l'orthocentre. Le triangle A'B'C' est formé avec les parallèles
aux côtés de ABC. De sorte que les hauteurs de ABC sont aussi les médiatrices
de A'B'C'. Les coordonnées trilinéaires de H sont: (HHa :
HHb : HHc). |
|
|
|
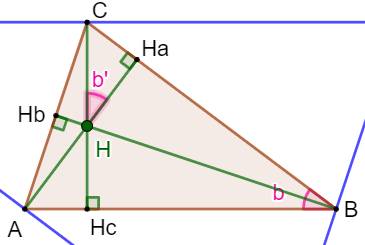
Mesure de la première coordonnée Dans le triangle rectangle CHHa puis dans le
triangle rectangle semblable BCHc. Notez que b = b' car ces deux angles ont le même
complémentaire en C.
|
|
|
|
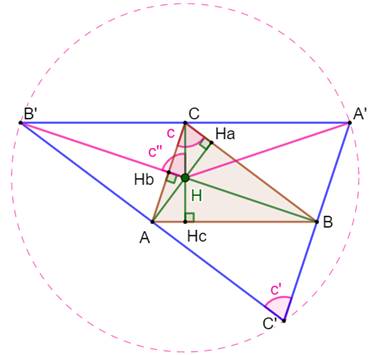
Mesure de CH Dans le triangle rectangle HCB':
Le grand triangle est inscrit dans un cercle car
H est le point de concours des médiatrices. Alors, comme ci-dessus: Du fait des parallèles: Bilan
|
|
|
|
Conclusion Avec H équidistant de A', B' et C': |
Coordonnées trilinéaires du centre
H
|
|
|
CT du centre
de gravité |
||
|
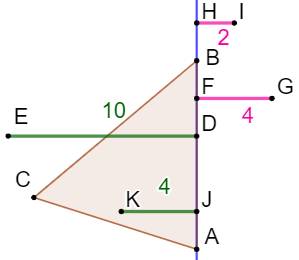
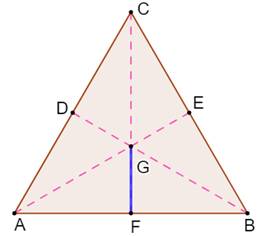
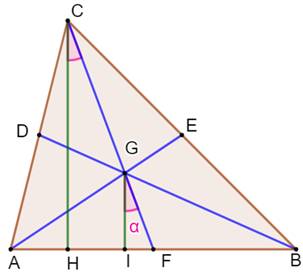
Construction de la figure Le centre de gravité G est le point de concours
es médianes. Le point G est situé aux (2/3 ; 1/3) de la médiane. On trace les deux perpendiculaires vertes. Les angles marqués en rose sont égaux
(congruents). La proportion sur la médiane se retrouve sur les
deux segments CH et GI (Thalès). Il s'agit d'évaluer GI
Soit une première expression des coordonnées
trilinéaires de G
En multipliant les CT de G par 3 et par l'une des
ces fractions en simplifiant:
|
Coordonnées trilinéaires du centre
G G ( AB · AC : BA · BC : CA · CB) |
|
Anglais
|
In geometry, the trilinear coordinates x:y:z of a
point relative to a given triangle describe the relative directed distances
from the three sidelines of the triangle. Trilinear coordinates are an example of
homogeneous coordinates. The ratio x:y is the ratio of the perpendicular
distances from the point to the sides (extended if necessary) opposite
vertices A and B respectively; the ratio y:z is the ratio of the
perpendicular distances from the point to the sidelines opposite vertices B
and C respectively; and likewise for z:x and vertices C and A. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Remarqua/Coordon.htm
|