|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
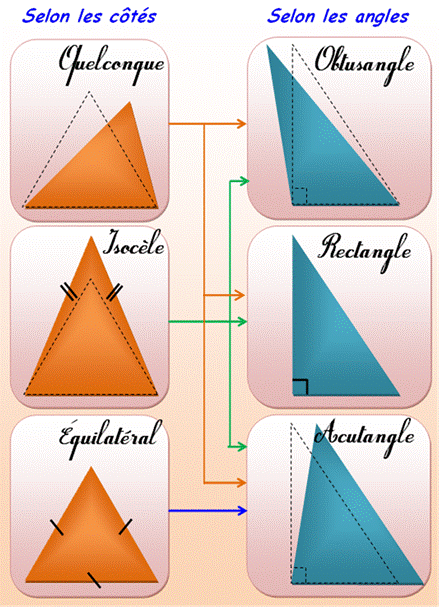
TYPES de TRIANGLES Le triangle est un polygone
à trois côtés, trois sommets et donc trois angles dont la somme vaut 180°. Le triangle de sommet A, B et C est noté: Sans particularités saillantes, il est dit quelconque.
Certaines familles de triangles sont définies en fonction des propriétés
des côtés et des angles. Objet de cette page. |
Humour

Source image: Grundy, Doug – Légende originale en anglais: "Nothing to worry about …
just a sprained ankle":
Rien de grave.. juste une entorse à la
cheville.
Voir
Pensées & humour
|
|
||
|
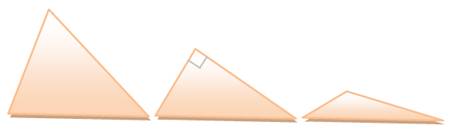
ACUTANGLE: trois
angles
aigus. RECTANGLE: un droit
et deux aigus. OBTUSANGLE: Un
obtus et deux aigus. |
|
|
Cas pathologiques
|
Un triangle ayant deux sommets confondus
est dégénéré. Il y a un angle plat et deux
angles nuls. Un triangle ayant ses trois sommets
alignés est un triangle plat. |
|
|
||
|
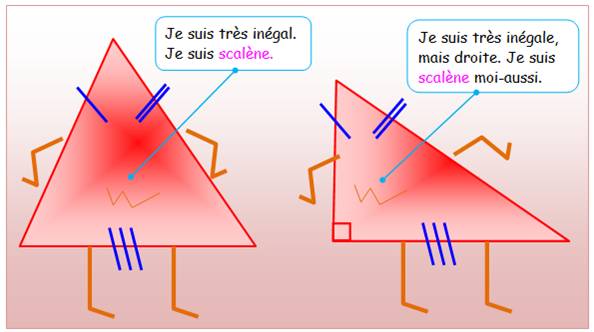
SCALÈNE: les trois
côtés sont de longueurs différentes, quels que soient les angles:
ISOCÈLE: deux
angles égaux. ISOCÈLE-RECTANGLE: isocèle et avec angle droit. ÉQUILATÉRAL: trois angles égaux; il trois fois isocèle; ses angles internes sont
égaux et valent 60°. |
Côtés de longueurs inégales
Scalène (quelconque) Scalène rectangle Deux ou trois côtés de mêmes longueurs
|
|
Merci à Raphaël L.G. pour ses
remarques pertinentes
Dans la famille SCALÈNE: le père et la mère.
|
|
||
|
Note: sans angle droit
un triangle est appelé triangle oblique. La somme des angles d'un triangle étant égale
à 180°, quelle que soit sa nature,
un triangle possède toujours deux angles aigus. Le triangle équilatéral est
acutangle avec ses trois angles valant 60°. |
|
|
Voir Partition du triangle obtusangle en triangles
acutangles
Cas du triangle rectangle
|
T. Rectangle scalène
si tous ses côtés sont de longueurs différentes. T. Rectangle isocèle ou demi-carré si deux côtés sont de mêmes
longueurs. T. Rectangle pythagoricien si les trois longueurs sont des nombres entiers; alors
a² + b² = c² . T. Rectangle des arpenteurs: côtés {3, 4, 5}. T. Rectangle des écoliers ou hémi-équilatéral: angles {30°, 60°, 90°}. T. Rectangle de Kepler si les longueurs des trois côtés sont en progression
géométrique. T. Rectangle d'or constituant
de l'étoile
à cinq branches. |
Voir détails en Triangle rectangle / Théorème de
Pythagore
|
|
||
|
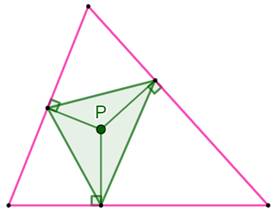
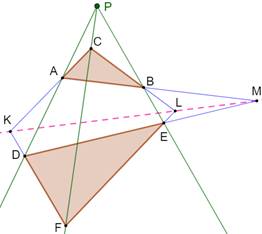
Triangle PODAIRE du point P Un
point P intérieur au triangle rose. Ses
projections orthogonales sur les côtés du triangle rose. Le
triangle vert est le triangle podaire de T. Triangle ANTIPODAIRE du point P Triangle
origine du triangle podaire Anglais:
pedal triangle and antipodal triangle. |
|
|
Ambiguïté avec l'anglais

D'après Clark Kimberling –
Expert en géométrie du triangle
|
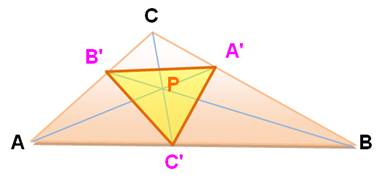
Triangle
PÉDAL (ou CÉVIEN) du point P Il est formé des
segments qui joignent les céviennes
concourantes d'un triangle. Voir Droite d'Euler du triangle pédal Triangle
ANTICÉVIEN du point P Triangle origine du
triangle pédal. Anglais: cevian triangle
and anticevian triangle. |
Triangles cévien et anticévien
A'B'C' est le triangle pédal de ABC ABC' est le triangle anticévien de
A'B'C' |
Voir Triangle
interne aux céviennes non concourantes (théorème de Routh)
|
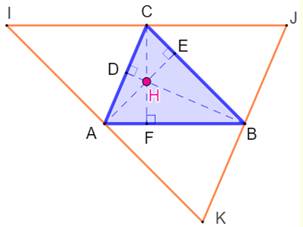
Triangle MÉDIAN (ou complémentaire) Triangle
pédal avec les médianes. Ce
triangle et le triangle origine sont semblables. Suite >>> |
Triangle médian
|
|
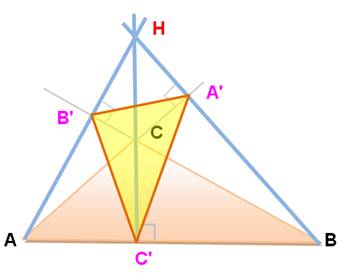
Triangle ORTHOCENTRIQUE ou ORTHIQUE Triangle
pédal dont les céviennes sont les hauteurs, celles-ci sont d'ailleurs les
bissectrices du triangle pédal Le
triangle orthocentrique est le triangle pédal de périmètre minimum. |
Triangle orthocentrique
Triangle pédal avec les hauteurs. |
|
Triangles
PERSPECTIVES Triangles dont les
sommets sont situés sur trois droites issues d'un même point. |
|
![]()
|
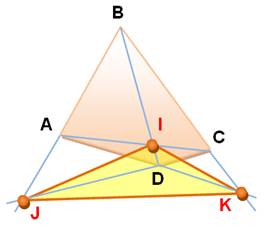
Triangle
HARMONIQUE d'un quadrilatère Triangle
formé par les points de concours des côtés du quadrilatère (J et K) et par le
point d'intersection des diagonales (I). |
Le quadrilatère ABCD donne le
triangle IJK |
Voir Autres triangles remarquables
|
PYTHAGORIEN HÉRONIEN AILLES |
|
Types de triangles selon les mesures
|
Triangles |
Côtés |
Aire |
Angles |
|
Entiers |
|
|
|
|
Entiers |
|
Un droit |
|
|
Rationnels |
Rationnels |
Rationnels |
|
|
Quadratique |
|
Rationnels |
Les angles aigus des triangles de
Pythagore sont transcendantaux.
|
TANGENTIEL HOMOLOGIQUES CALABI HEILBRONN SIERPINSKI CURVILIGNE SPHÉRIQUE |
|
|
Triangle
de REULEAUX |
|
|
Triangle
d'OR |
|
|
Triangle
de Penrose |
|
|
||
|
Autres triangles Humour
Le bermuda vient
effectivement des îles Bermudes |
Suite et explications >>> Voir aussi Expression avec le mot
"triangle" |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgType.htm |
![]()