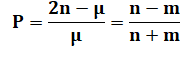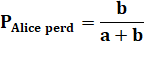|
Édition du: 29/03/2023 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
CHEMINS sur GRILLE / RÉSEAU Domaines
des graphes
et de la combinatoire.
On dit chemin ou trajectoire
(path) On dira grille ou réseau
ou quadrillage ou graphe
ou même échiquier. Notez que
treillis à une signification
particulière en maths. Divers types:
chemins en escalier, chemins avançant seulement vers le droite ou vert le
haut, chemins qui, en plus, permettent le trajet diagonal, … Chemins
contenus dans une portion de la grille, en dessous d'une diagonale par
exemple. Combien
de chemins possibles pour relier deux points de la grille ? Sujet de
combinatoire qui fait l'objet de nombreuses études théoriques tant ce domaine
est complexe, mais recélant de nombreux cas
d'applications. |
||
|
|
Sommaire de cette page >>> Chemin sur grille ou chemin sur réseau >>> Cas historique: le vote >>> Cas historique: la ruine du joueur |
Débutants Glossaire |
|
On dit chemin
ou trajectoire. La progression unitaire est appelée: pas Parcourir la grille On se donne un quadrillage régulier dit grille ou
réseau (anglais: grid or lattice). On dessine une ligne brisée qui relie certains
points du quadrillage: c'est un chemin de grille (anglais (lattice path). Il
peut être orienté ou non. Selon les contraintes de parcours, il existe plus
ou moins de chemins pour relier deux points en passant par les points de la
grille. Comment calculer la quantité des chemins possibles ? |
Pionnier – 1889 L'officier français, mathématicien amateur et aussi historien Henri
Auguste Delannoy est connu pour avoir étudié
ces chemins de réseau notamment via le mouvement de la tour sur un
échiquier de formes diverses. Nombreuses applications des chemins sur grille: marche
aléatoire, fractions continues, arbres, cartes planes, mots et caractères,
pavages, … et, de nombreux développements en mathématiques avancées comme la
combinatoire de dénombrement, la combinatoire algébrique, combinatoire asymptotique, physique
combinatoire, théorie des probabilités, algèbre de calcul par ordinateurs,
… |
|||||
|
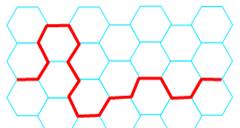
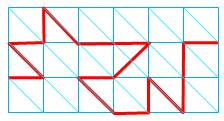
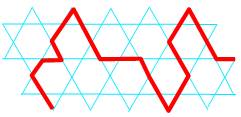
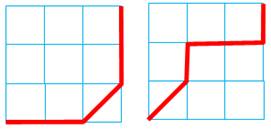
Quelques exemples de réseaux
(bleus) et chemins (rouges)
|
||||||
|
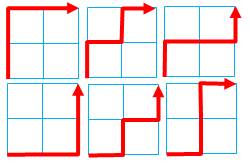
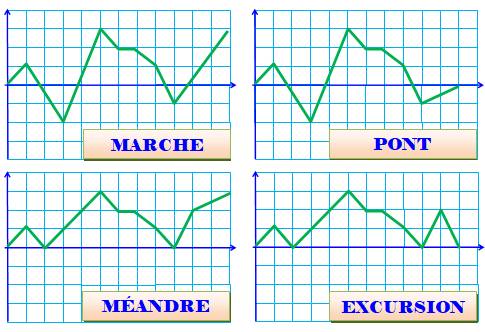
Types de chemins sur grilles classiques
(rectangulaires)
Tous les chemins partant du point (0,0). À
gauche, ils se terminent en (n, k) et à droite en (n, 0). En haut chemins positifs et négatifs; en bas,
toujours positifs. |
||||||
Voir Brève
49-974
|
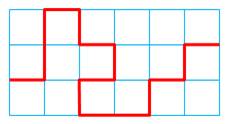
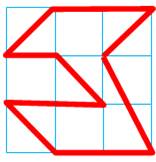
Chemins généralement étudiés Les chemins auto-évitants
(CAE): il ne passe jamais deux fois sur le même point. Comme les serpents,
ils ne se mordent jamais la queue. Imaginez que vous vous promeniez dans une ville
dont le plan est un quadrillage régulier (Manhattan), en vous interdisant de
passer plus d’une fois à chacun des carrefours. Un tel chemin s'il est fermé
(illustration) est un polygone
auto-évitant. (PAE). Les CAE ont été introduits en 1948 par le
chimiste Paul Flory (prix Nobel 1974) dans le but de modéliser le
comportement des polymères plongés dans un solvant |
|
|
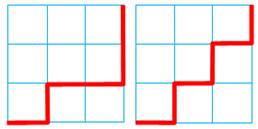
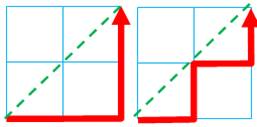
Escalier (staircase walk) Un modèle particulièrement étudié est en forme
d'escalier. Progression vers la droite ou vers le haut; sans retour en
arrière. On ne fait pas attention à la hauteur de la
marche ! Imaginez la tour aux échecs qui partirait du coin
bas-gauche et progresserait sans revenir en arrière vers le coin haut-droit. Voir Chemins de
Manhattan |
|
|
Diagonale La progression selon la diagonale montante est
permise. Voir Nombres de Delannoy |
|
|
Contraint par la diagonale Le chemin ne doit jamais passer au-dessus de la
diagonale montante. Voir Chemins de Dyck / Nombres de Schröder |
|
|
Condition du vote
On demande la probabilité que, durant le
dépouillement des voix, le nombre de voix pour A soit toujours supérieur au nombre de voix pour B. Résolution Ce problème a été résolu en utilisant des chemins
sur des réseaux dans le plan. Il est considéré comme le point de départ de la
théorie des chemins sur réseau. |
Théorème du premier tour (first
ballot theorem) En 1887, Joseph
Bertrand publie la réponse dans les Comptes rendus de l'Académie des Sciences: La probabilité est donnée par cette formule:
|
||
|
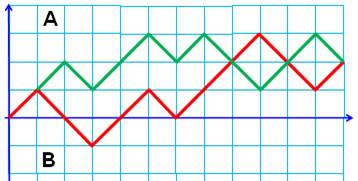
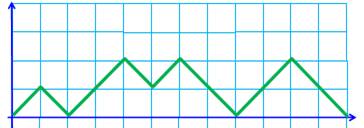
Réseau Pour représenter les votes, on utilise un réseau orthonormé,
un système d'axes avec coordonnées
entières. En commençant par l'origine, chaque vote est représenté
un cran plus loin en abscisse avec un trait oblique dans la direction du
gagnant: vers le haut pour A et vers le bas pour B. Dans les deux cas (vert et rouge), c'est A qui
gagne au final par deux voix d'avance. Mais, seul le chemin vert répond à l'hypothèse:
toujours supérieur. Réseau de Dyck Cas particulier ou le chemin est supérieur, passe
par des nuls et se termine par un nul. Ce sont des chemins
de Dyck (Dyck paths). SUITE en Réseaux de Dyck |
Graphique témoignant du vote par
douze votants
Exemple de réseau de Dick
|
||
|
Historique Lettre de Blaise Pascal à Pierre Fermat en 1656. Ruine du joueur (gambler's ruin
problem) façon Huygens Chaque joueur commence avec 12 points. Un lancer
est réussi si le premier joueur fait 11 et, c'est 14 pour le second. Un lancer réussi ajoute un au score de ce joueur
et soustrait un du score de l'autre joueur. Le perdant du jeu est le premier à atteindre zéro
point. Quelle est la probabilité de victoire de chaque
joueur ? |
Ruine du joueur façon
historique Alice et Bob, jouent à pile ou face. Alice commence le jeu avec a euros et Bob
avec b euros. La partie se termine dès qu'un des joueurs est sans le sou. Règles: les joueurs lancent une pièce à tour de
rôle. À chaque tour, le gagnant reçoit un euro du perdant.
|
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |