|
|||||||||||||||||||||||||||||
![]()
|
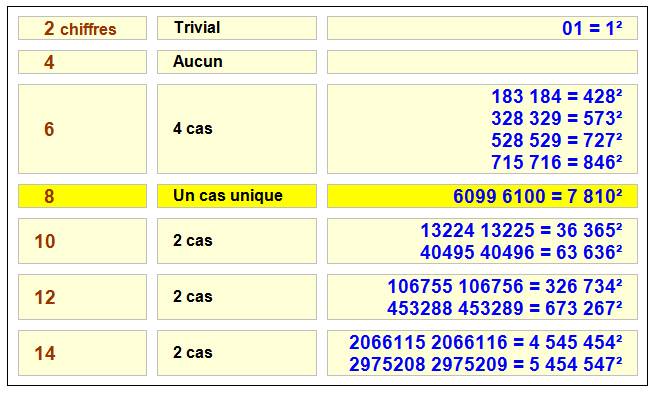
CONCATÉNATION de deux nombres CONSÉCUTIFS formant
un CARRÉ Deux nombres consécutifs
accolés qui forment un carré. Unique cas pour 8 chiffres. Une bonne occasion de tester
notre esprit de déduction |
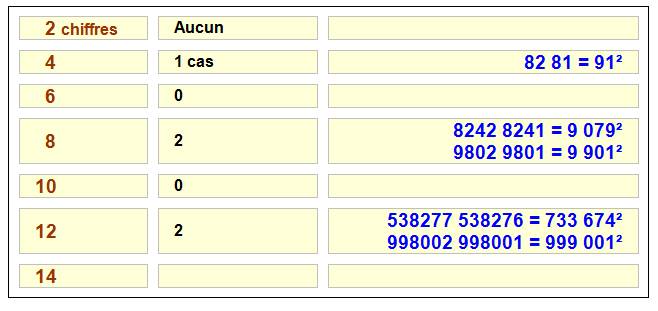
Carrés
des nombres à deux chiffres
|
91² = 8182 avec 81 = 82 – 1 Aucun
autre tel motif avec différence de 1 dans un sens ou l'autre et même avec
égalité. Il faut créer un écart de 4 pour trouver le suivant: 81² = 6561 et 65 = 61 + 4 On
oublie le motif trivial: 20² = 400 avec 4 = 0 + 4
Avec
un écart de 5 on trouve: [45,
2025], [46, 2116], [55, 3025], [56, 3136] |
|
|
|
|
Carrés
formés de la concaténation de deux nombres successifs
Voir
Nombre 6099 6100 Carrés formés de la concaténation de deux
nombres successifs INVERSES (le second est inférieur au premier)
|
|
Voir Suite et autres puissances
|
|
||||||||||||
|
Deux
catégories de méthodes
Sur
un tableur Pour
deux chiffres commencez par mettre 10 en A et les formules indiquées dans les
colonnes suivantes:
Marquez
cette ligne et accrochez l'ancre en bas à droite Tirez
jusqu'à l'indication 98 C'est
terminé, vous avez toutes vos réponses Adaptez
pour 4, 6, 8 … chiffres Avec
un programme, comme Mapple
Note: l'évaluation de
la racine avec evalf, permet de limiter le temps de calcul avec un
test sur 10 décimales seulement. Lorsque vous explorerez des nombres avec plus
de chiffres vous devrez sans doute calculer RN avec RN := sqrt(N). |
||||||||||||
Voir Programmation
|
|
|
|
Deux
nombres consécutifs accolés qui forment un carré, unique cas pour 8 chiffres.
Comment s'y prendre pour le trouver? |
|
|
Recherche d'une formulation en facteurs |
||
|
|
N |
=
a² |
|
|
N a |
< 100 000 000 < 10 000 |
|
|
N |
=
[n] [n+1] |
|
|
|
=
10 000 n + n + 1 =
10 001 n + 1 |
|
|
a² |
=
10 001 n + 1 |
|
|
10 001 n |
=
a² – 1 |
|
10 001 n |
=
(a – 1)(a + 1) |
|
|
Recherche des facteurs – Première tentative: simple |
||
|
|
10 001 n |
=
(a – 1)(a + 1) |
|
|
10 001 10 002 |
=
a – 1 =
a |
|
|
10 001 10 000 |
=
a + 1 =
a |
|
Recherche des facteurs – Deuxième tentative: un peu plus
recherchée |
||
|
|
10 001 n |
=
(a – 1)(a + 1) |
|
|
73 x 137 n |
=
(a – 1)(a + 1) |
|
|
73 74 |
=
a – 1 =
a |
|
|
73 x 137 n n |
=
(74 – 1)(74 + 1) =
73 x 75 = 5 475 =
5 475 / 10 001 Impossible |
|
|
137 138 |
=
a – 1 =
a |
|
|
73 x 137 n n |
=
(138 – 1)(138 + 1) =
137 x 139 = 19 043 =
19 043 / 10 001 Impossible |
|
Recherche des facteurs – Troisième tentative Hélas,
il faut recourir à des outils plus complexes! |
||
|
|
73 x 137 n |
=
(a – 1)(a + 1) |
|
|
73u x 137v |
=
(a – 1)(a + 1) |
Choix
équations
|
|
73u 137v |
=
a – 1 =
a + 1 |
|
|
137v – 73u |
=
2 |
|
|
v |
=
(73u + 2) / 137 |
|
|
u = 30 v = 16 |
Vérification (73
x 30 + 2) / 137 = 2192 / 137 = 16 |
|
NON |
n = u v |
=
480 Que
trois chiffres (n doit en avoir 4) |
Mêmes
équations
|
NON |
u = 167 v = 89 |
n
= 167 x 89 = 14863 Nombre
à 5 chiffres (n a 4 chiffres seulement) |
Autres
équations
|
|
73u 137v |
=
a + 1 =
a – 1 |
|
|
137v – 73u |
=
– 2 |
|
|
v |
=
(73u – 2) / 137 |
|
|
u = 107 v = 57 |
Vérification (73
x 107 – 2) / 137 = 7809 / 137 = 57 |
|
BINGO! |
n = u v N = |
=
107 x 57 = 6099 =
6099 6100 =
7810² |
C'est une solution.
Est-ce la seule?
Mêmes
équations
|
|
u = 244 v = 130 |
n
= 244 x 130 = 31720 Trop
grand pour n (4 chiffres seulement) |
FIN
d'exploration
|
N |
= 6099 6100 = 7810² |
Seule
solution |
![]()
|
Voir |
|
|
DicoNombre |
|
|
Livre |
J'ai
retrouvé le nombre 60996100 dans le livre de
Louis
Thépault . Il comporte de nombreux autres cas avec leur résolution.
Passionnant! |
|
Cette page |
![]()