|
||||||||||||||||||||||||||||||||||||
![]()
|
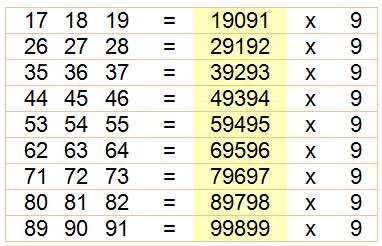
PALINDROMES et nombres/chiffres CONCATÉNÉS 121314 n'est pas un nombre palindrome, bien sûr. 171819 peut le devenir en le divisant par 9: 19091. Pourtant ces cas sont très rares. |
|
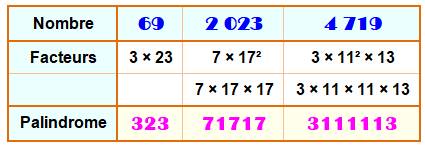
Définition PF Un
nombre palindrome-facteurs (PF) est un
nombre dont les chiffres de TOUS les facteurs concaténés forment un
palindrome. |
Exemples
|
||
|
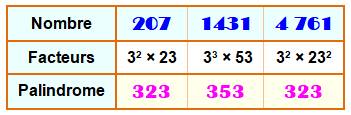
Définition PJF Un
nombre palindrome-jeu de facteurs (PJF)
est un nombre dont les chiffres du jeu de facteurs (sans les exposants)
concaténés forment un palindrome. |
Exemples
|
||
|
Liste PF jusqu'à 5000 |
1, 4, 8, 9, 16, 25, 27, 32, 39, 49,
64, 69,
81, 119,
121, 125, 128, 129, 159, 219,
243, 249,
256, 259,
329,
339,
343, 403, 429, 469, 507,
512, 625, 669,
679,
729, 795,
1024, 1207, 1309, 1329, 1331, 1533, 1547, 1587, 1589, 1703, 2023, 2048,
2097, 2187, 2319, 2321, 2359, 2401, 2649, 2701, 3039, 3125, 3421, 3503, 3629,
3633, 3639, 3729, 3897, 3899, 3975, 4096, 4303, 4607, 4719, 4839, … |
||
|
Liste PJF non PF Parmi eux, les nombres premiers palindromes. |
2, 3, 5, 7, 11, 101, 117, 131, 151, 181, 191,
207, 313, 351, 353, 373, 383, 387, 477, 621, 657, 727, 747, 757, 787, 797,
833, 919, 929, 1017, 1053, 1161, 1287, 1431, 1521, 1813, 1863, 1971, 2007,
2241, 2303, 2385, 3051, 3159, 3283, 3483, 3861, 3987, 4293, 4563, 4599, 4753,
4761, … |
||
|
Commentaires |
Sur cette plage de nombres, tous les PF sont
également PJF, sauf deux: 2097 = 3² ×233 est PF (33233) mais pas PJF (3233) 3897 = 3² ×433 est PF (33433) mais pas PJF (3433) |
||
Voir Brève
48-944
Liste jusqu'à 2023 avec facteurs et le palindromes associés
|
n |
Facteurs |
Palindrome |
n |
Facteurs |
Palindrome |
|
1 |
|
0 |
329 |
[7,1] , [47,1] |
747 |
|
4 |
[2,2] |
22 |
339 |
[3,1] , [113,1] |
3113 |
|
8 |
[2,3] |
222 |
343 |
[7,3] |
777 |
|
9 |
[3,2] |
33 |
403 |
[13,1] , [31,1] |
1331 |
|
16 |
[2,4] |
2222 |
429 |
[3,1] , [11,1] , [13,1] |
31113 |
|
25 |
[5,2] |
55 |
469 |
[7,1] , [67,1] |
767 |
|
27 |
[3,3] |
333 |
507 |
[3,1] , [13,2] |
31313 |
|
32 |
[2,5] |
22222 |
512 |
[2,9] |
222222222 |
|
39 |
[3,1] , [13,1] |
313 |
625 |
[5,4] |
5555 |
|
49 |
[7,2] |
77 |
669 |
[3,1] , [223,1] |
3223 |
|
64 |
[2,6] |
222222 |
679 |
[7,1] , [97,1] |
797 |
|
69 |
[3,1] , [23,1] |
323 |
729 |
[3,6] |
333333 |
|
81 |
[3,4] |
3333 |
795 |
[3,1] , [5,1] , [53,1] |
3553 |
|
119 |
[7,1] , [17,1] |
717 |
1024 |
[2,10] |
2222222222 |
|
121 |
[11,2] |
1111 |
1207 |
[17,1] , [71,1] |
1771 |
|
125 |
[5,3] |
555 |
1309 |
[7,1] , [11,1] , [17,1] |
71117 |
|
128 |
[2,7] |
2222222 |
1329 |
[3,1] , [443,1] |
3443 |
|
129 |
[3,1] , [43,1] |
343 |
1331 |
[11,3] |
111111 |
|
159 |
[3,1] , [53,1] |
353 |
1533 |
[3,1] , [7,1] , [73,1] |
3773 |
|
219 |
[3,1] , [73,1] |
373 |
1547 |
[7,1] , [13,1] , [17,1] |
71317 |
|
243 |
[3,5] |
33333 |
1587 |
[3,1] , [23,2] |
32323 |
|
249 |
[3,1] , [83,1] |
383 |
1589 |
[7,1] , [227,1] |
7227 |
|
256 |
[2,8] |
22222222 |
1703 |
[13,1] , [131,1] |
13131 |
|
259 |
[7,1] , [37,1] |
737 |
2023 |
[7,1] , [17,2] |
71717 |
Notez la présence de la
puissance des chiffres (16, 25, 27 …);
|
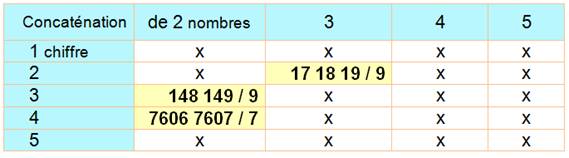
3
nombres de 2 chiffres |
|
|
|
|
|
|
|
|
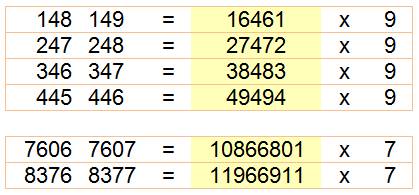
Il n'en existe que six avec deux nombres à n chiffres, ou
76067607 /7 = 10866801(quatre chiffres).
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()