NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	ÉNIGMES				Glossaire Général
INDEX JEUX	Classiques	Famille	Famille 8	K fois l'âge
		Famille (Suite)	Avec le cousin
		Sommaire de cette page >>> Énigme >>> Méthode >>> Graphe >>> Solution – Le graphe >>> Résolution

Énigme ancienne avec résolution express – Pour vous tester.

Énigme

J'ai deux fois l'âge que vous aviez quand j'avais l'âge que vous avez, mais lorsque vous aurez mon âge, nous aurons ensemble 90 ans.

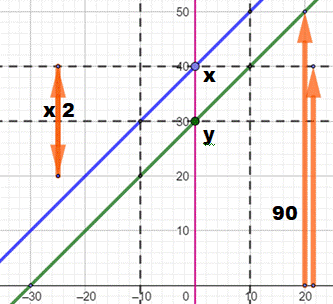
Solution

Avec x mon âge et y l'âge de l'autre.

Différence d'âge: d = x – y

Énoncé 1: x = 2(y – d) = 2(2y – x) = 4y – 2x => 3x = 4y

Énoncé 2: (x + d) + (y + d) = 3x – y = 90

Calcul: 4y – y = 9 0 => 3y = 90 => y = 30 et x = 40.

Illustration

En 0, le temps présent. Droite bleue et droite verte = temps qui passe pour chacun.

Les deux parties de l'énoncé sont visualisées par les vecteurs orange.

ÉNIGME
Quand mon fils aura 15 ans de plus qu'il n'a aujourd'hui, il aura l'âge que j'avais quand j'avais 8 fois son âge. Quand il aura atteint l'âge que j'ai aujourd'hui, nous aurons ensemble, si je suis encore de ce monde, 31 fois l'âge qu'il avait quand j'avais 8 fois son âge. Quel est alors l'âge du fils de cet homme?

MÉTHODE

Je vous propose une méthode générale pour résoudre ce genre de problème. Bien sûr, il possible de suivre un raisonnement et trouver astucieusement la solution. Mon but ici est de donner la possibilité à tous de trouver la solution par une méthode systématique. Méthode qui est applicable à d'autres problèmes plus complexes et, en prime, avec cette méthode vous avez ce qu'il vous faut pour inventer vous-même de telles énigmes! Voir Autre énigme résolue avec cette méthode

GRAPHE

Dessinez un repère classique à deux axes: abscisses: le temps qui s'écoule; et ordonnées: l'âge des individus. Les deux lignes rouges représentent l'âge de chacun lorsque le temps s'écoule: Nous avons placé la naissance du père à l'origine. Celle du fils, évidemment, quelques années plus tard. 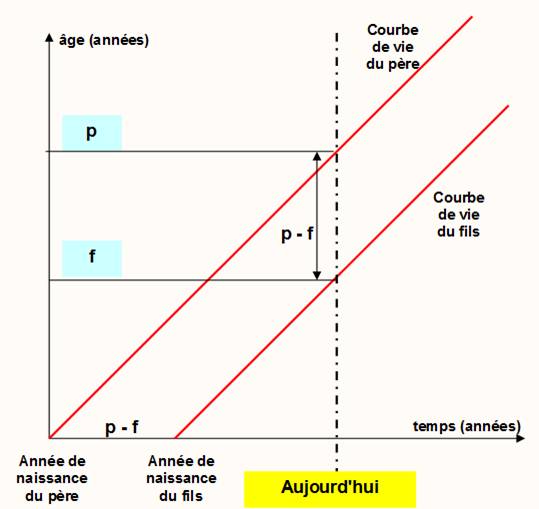Aujourd'hui (cette année), trait pointillé vertical le père a un âge noté p le fils un âge noté f Notons que: la différence d'âge (p-f) , segment fléché vertical est égale à la différence entre les années de naissance. Normal les droites de vie sont des obliques à 45° (un anniversaire tous les ans!) Pouvez-vous trouver la solution avec ce graphe ?

SOLUTION – Le graphe

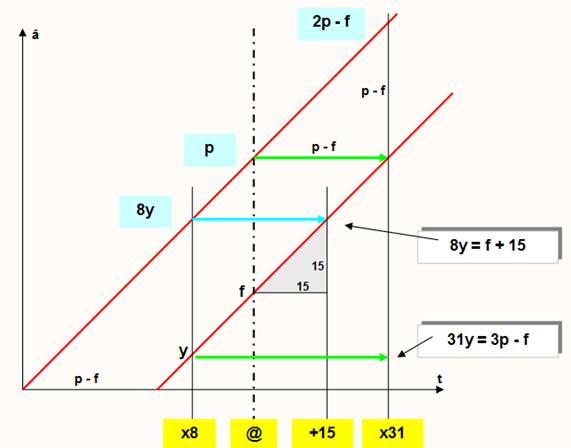
Le premier trait vertical (x8) montre l'année où l'âge du père vaut 8 fois celui du fils (noté y). Le deuxième, l'année courante (@ comme aujourd'hui). Le troisième matérialise le + 15 ans; cette année-là, le fils a l'âge 8y (flèche bleue). La première proposition se met alors en équation. Quand mon fils aura 15 ans de plus qu'il n'a aujourd'hui, il aura l'âge que j'avais quand j'avais 8 fois son âge. Soit: 8y = f + 15. Ici, nous pouvons remarquer une autre relation importante à satisfaire l'écart entre les âges père et fils est toujours le même: 8 y – y = p – f. Le quatrième segment vertical (x31) donne ce qui se passe lorsque mon fils aura l'âge que j'ai aujourd'hui (flèche verte) l'âge du fils est bien évidemment p celui du père est p + (p – f) = 2p – f leur somme père et fils donne: 3p – f La seconde proposition se met alors en équation. Quand il aura atteint l'âge que j'ai aujourd'hui, nous n'aurons ensemble, si je suis encore de ce monde, 31 fois l'âge qu'il avait quand j'avais 8 fois son âge. Soit: 31y = 3p – f.

RÉSOLUTION

Nous avons un système de trois équations à 3 inconnues (p, f et y)	8y 7y 31y	= f + 15 = p – f = 3p – f
Ajoutons les équations 1 et 3	39y	= 3p + 15
Calculons p	p	= 13y – 5
Et f, à partir de la première équation	f	= 8y - 15
Calculons p – f	p - f	= 5y + 10
À comparer à l'équation 2	p - f	= 7y
En égalisant	7y	= 5y + 10
Et finalement la valeur de y	y	= 5
Qui permet de calculer les âges demandés	fils père	= 25 = 60
On vérifie que le père n'est pas trop âgé lors de la comparaison en x31 puisqu'il aura	2p – f	= 95

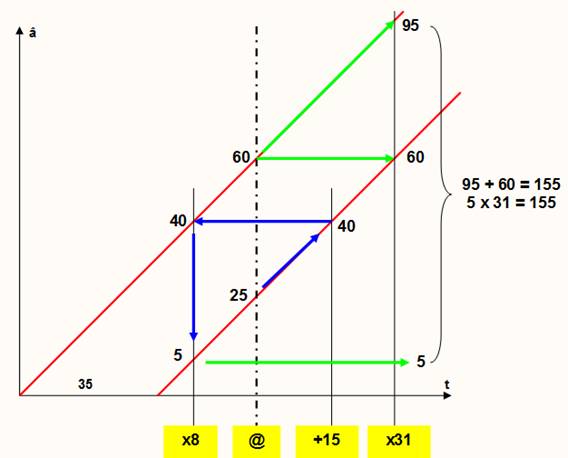
Illustration chiffrée de la réponse

Suite	Voir haut de page
Voir	Jeux – Index Logique – Index
Cette page	http://villemin.gerard.free.fr/Puzzle/EnigFam8.htm