|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Deviner mon âge et celui de … Une série d'indices pour deviner mon
âge, celui de mon ami et celui de mon cousin. La résolution se prête bien à l'établissement
d'équations
plutôt qu'un
graphe en fonction du temps. Cette
énigme m'a
été proposée par Christian ZZ que je remercie. |
|
|
||
|
Le premier, un matheux, déclare: |
L'autre, également matheux répond: |
|
|
|
Votre âge actuel est égal à 10 fois notre
différence d'âge.
Quand la somme de vôtre âge, et de l'âge de votre
cousin était égale à 4 fois mon âge, figurez vous que le total de nos âges
d'alors, c'était vôtre âge actuel. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
À la lecture de l'énoncé, on peut établir ce tableau
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
On retient les neuf équations du tableau précédent. On remarque que, s'agissant de trouver sept inconnues, deux équations
sont redondantes.
Les deux
équations (5) et (6) sont redondantes.
Il est possible de résoudre l'énigme sans elles. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La résolution en fonction de "s" montre qu'il existe
plusieurs solutions avec s = 3k. C'est-à dire le moment où on situe la belle
époque. Avec k = 5, on situe la belle époque il y a 15 ans. Exemples de solutions en jaune et, en jaune foncé, celle
préconisée par l'auteur de l'énigme.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vérification |
|
|||||||||||||||||||||||||||||||||||
|
Avec la solution (50, 45, 60), on reprend le tableau initial. Ce tableau peut être consulté pour vérifier que les formules établies
à partir de l'énoncé sont correctes.
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
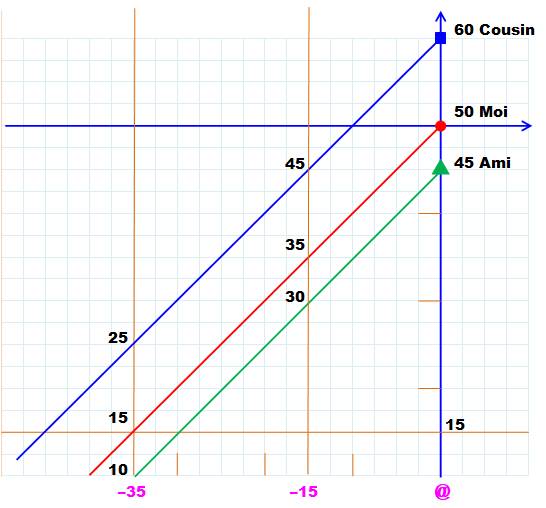
En abscisse, le temps qui passe, avec la date actuelle (@) à droite. En ordonnée, l'âge des trois personnes, avec mon âge (50 ans) à la
croisée des axes bleus. En oblique, les droites de vie des trois personnages.
Il est bien sûr possible de conduire la résolution de l'énigme à
partir de ce graphique. Exemple
Tout cela se
passait il y a 35 ans (verticale ocre de gauche). |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()