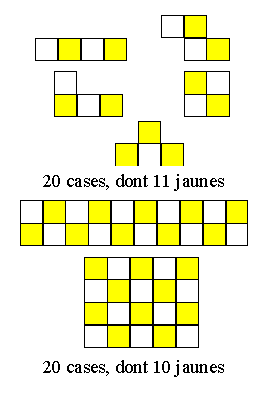|
||||||||||||||||||||||||||||||||||||||||
![]()
|
N–OMINOS Inventaire. |
|
|
||
|
Domino:
combinaison de carrés |
2 |
|
|
Nombre
|
1 |
|
|
Surface
totale |
2 |
|
|
On peut couvrir tout l'échiquier avec des dominos. Mais, impossible de couvrir l'échiquier
tronqué Voir dominos |
||
|
|
||
|
Triomino: combinaison de carrés |
3 |
|
|
Nombre |
2 |
|
|
Surface totale |
6 |
|
|
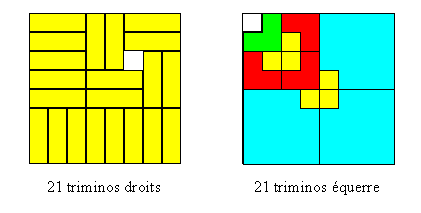
Constructions avec trou monomino
Les 3 quadrants
bleus sont construits comme le quadrant haut gauche. |
||
|
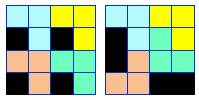
2023 Quantité de façons de paver un carré
4×4 en utilisant de 1 à 4 fois le triomino
en L. Voir Number
2023 – Numbers Aplenty |
Deux exemples de tels pavages
|
Voir DicoNombre
2023
|
|
||
|
Tétromino: combinaison de carrés |
4 |
|
|
Nombre |
5 |
|
|
Surface totale |
20 |
|
|
Couverture
du rectangle Les trétominos ne permettent pas de couvrir une forme
rectangulaire. Rectangles possibles : 2 x 10 ou 5 x 4. Par le décompte des cellules blanches et jaunes,on
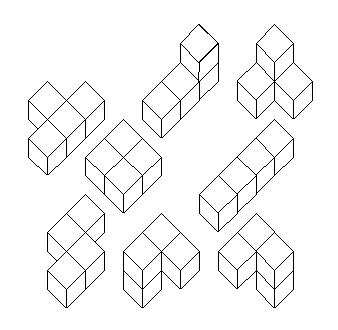
montre l'impossibilité: Tétrominos
en relief
Rectangle
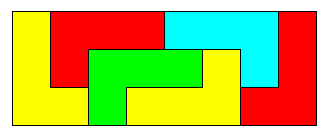
minimum avec des quadriminos en L Rectangle 3 x 8
avec 6 L
|
||
|
|
||
|
Pentomino: combinaison de carrés |
5 |
|
|
Nombre |
12 |
|
|
Surface totale |
60 |
|
|
Chaque pentamino est
baptisé par une lettre qui rappelle sa forme. |
||
|
|
||
|
Hexomino: combinaison de carrés |
6 |
|
|
Nombre |
35 |
|
|
Surface totale |
210 |
|
|
Faisabilité 210 = 3 x
70 = 5 x 42 = 6 x 35 = 7 x 30 = 10 x 21 = 15 x 15 Il n'existe aucune solution pour former l'une de ces
surfaces avec les hexominos. |
||
Voir Page spéciale hexominos – Tous les types
|
|
|||||||||||
|
Heptomino: combinaison de carrés |
7 |
||||||||||
|
Nombre |
108 |
||||||||||
|
Surface totale |
756 |
||||||||||
|
Dont, creux |
1 |
||||||||||
|
Et c'est le plus petit polyomino creux:
|
|||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()