NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/10/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	POLYOMINOS				Glossaire Général
INDEX Jeux	Polyominos	N-ominos	Dominos	Pentaminos
				Hexominos
		Sommaire de cette page >>> Les 12 pièces du jeu de pentamino >>> Rectangles >>> Dénombrement >>> Autres formes dans le monde pentamino >>> Surfaces à trous >>> Pyramides >>> Relief

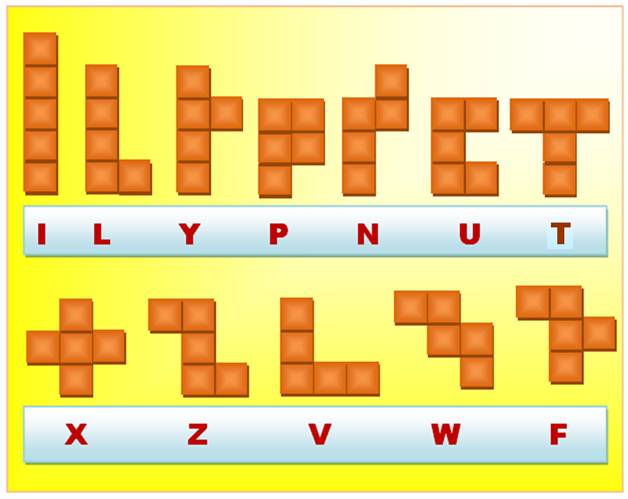
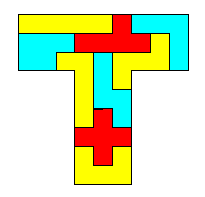
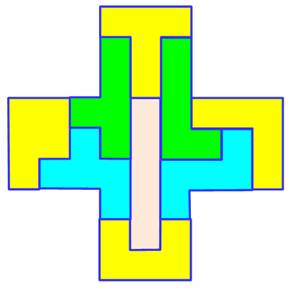
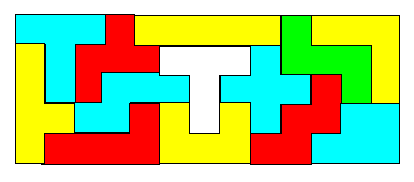
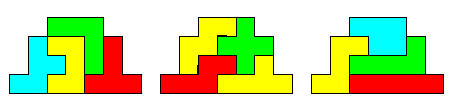
PENTAMINOS ou PENTOMINOS

On peut les réaliser facilement avec du carton ou des bouts de bois – ils existent aussi tout fait dans le commerce.

On passe des heures à essayer de trouver une des très nombreuses solutions à ce puzzle qui semble si simple et … on finit par aller voir la solution! Voici quelques une d'entre-elles.

Les 12 pièces du jeu de PENTAMINO

Il n'existe que douze formes de pentaminos, polygone formé par assemblage de cinq carrés identiques. La surface couverte par ces douze pentaminos est de: 12 x 5 = 60 petits carrés.

Chaque pentamino porte un nom de lettre qui lui ressemble (approximativement):

Chacune des formes du pentamino nécessite 12 traits (allumettes).
Sauf le P qui se dessine avec 10 allumettes. Ou 16 et 15 en comptant les traits internes.

Deux pièces qui se superposent par retournement, et rotation éventuelle, sont dites identiques.

Retournement possible I U T X V W

Impossible à retourner L Y P N Z F

Note: nous parlons de la pièce pentamino; pas de la lettre elle-même!

La W nécessite une rotation de 180°.

Sans cette convention, il y aurait 18 pentaminos.

RECTANGLES
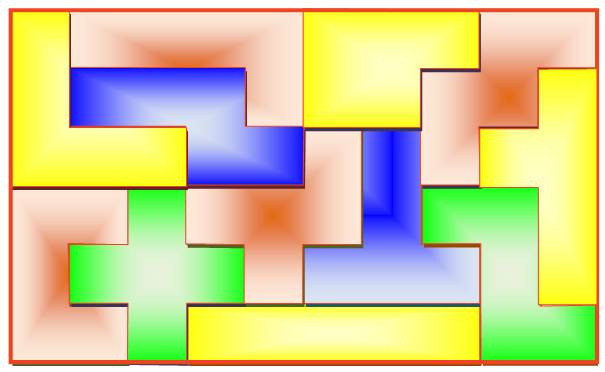
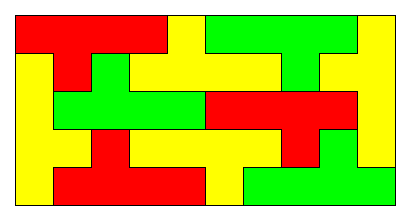
Rectangle 6 x 10 Rectangle 6 x 10 en 2 fois 6 x 5 Si les pièces sont blanches d'un côté et noires de l'autre, il est possible de faire couvrir ce rectangle tout en noir ou tout en blanc à l'exception d'une pièce, le L.

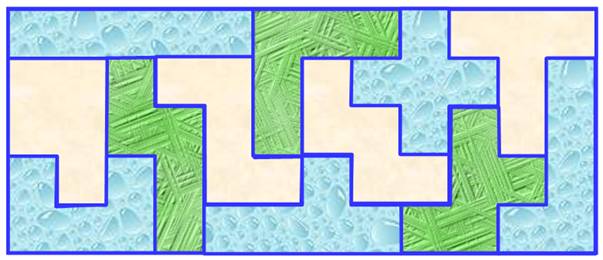
Rectangle 5 x 12

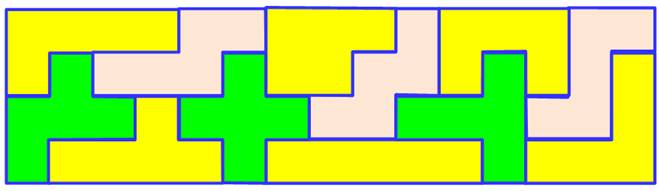
Rectangle 4 x 15

Rectangle 3 x 20 – Les deux seules solutions

Dénombrement

Le tableau donne le nombre de solutions différentes, sans compter les solutions symétriques, selon la taille du rectangle:

Taille du rectangle	Quantité de solutions
6 x10	2 339
5 x 12	1 010
4 x 15	368
3 x 20	2

On peut aussi construire un parallélépipède de 3 x 4 x 5 = 60.
Il y a 3 940 solutions.

AUTRES FORMES en restant dans le monde pentamino
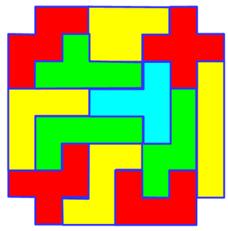
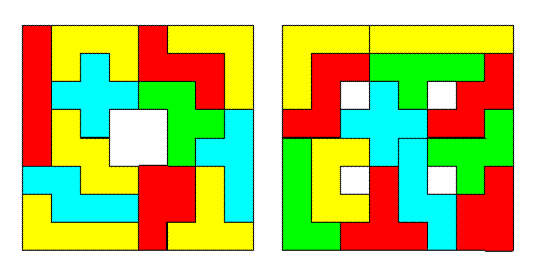
Triplication du pentamino Autre problème classique du pentamino: faire un des pentaminos à l'échelle 3, avec 9 pièces, en excluant la pièce tripliquée et deux autres à trouver. Surface 9 x 5 = 45. Rectangle à trou pentamino On peut faire un rectangle 5 x 13 = 65 en doublant une des pièces: Formes identiques Rectangle minimum avec des pentaminos en Y Rectangle 10 x 5 avec 10 Y

SURFACES à trous
ÉCHIQUIER: Carré 8 x 8 avec 4 trous Échiquier: 64 cases. Pentaminos: 60 carrés. Soit 4 cases non couvertes. Rectangle 7 x 9 avec 3 trous Rectangle 3 x 21 avec 3 trous

PYRAMIDES (Escaliers)

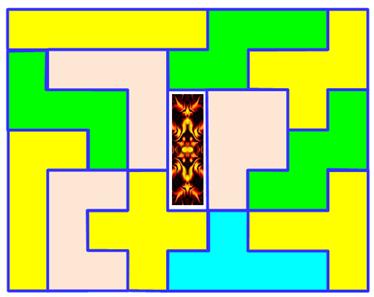
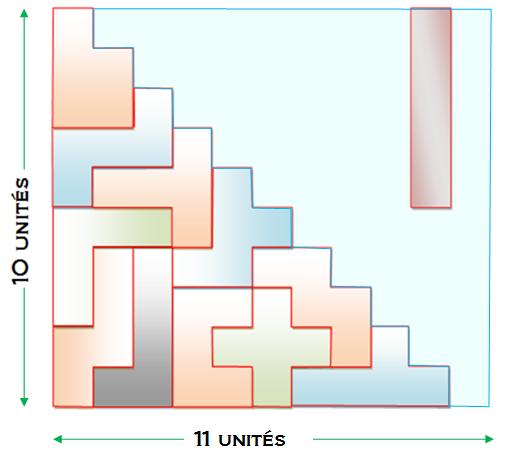
Il s'agit de former une pyramide (en fait un triangle rectangle avec hypoténuse en escalier) dont les côtés mesurent 10 et 10. Il est toujours possible de construire cet escalier en laissant de côté l'une quelconque des pièces du pentamino, sauf le W et le P. Il existe 224 solutions. Voici une solution sans utiliser le pentamino "I": La surface (aire) vaut; En utilisant deux fois la même forme encastrées l'une dans l'autre, on forme un rectangle de 10 x 11, soit l'aire de l'escalier: ½ (10 x 11) = 55. L'aire se vérifie aussi ainsi: l'aire de chaque pièce vaut 5. Il y ne a 11. L'aire totale est égale à: 5x 11 = 55.

Merci à Odette De M. pour ses observations

RELIEF

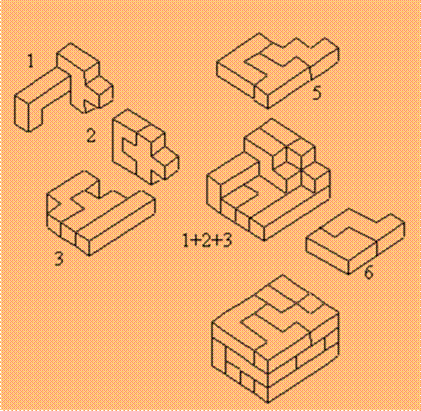
Parallélépipède 3 x 4 x 5 Une des 3 940 solutions: Bien d'autres formes sont réalisables, comme, chaque lettre du pentamino en relief sur une épaisseur de 3 et une surface de 20. Réalisable pour toutes les pièces du pentamino sauf le W et le X. Il y a même 1082 solutions pour former le P; mais une seule pour le F. Il est possible de réaliser un escalier 5 x 5 x 4: 5 marches et 5 contremarches; avec des marches de 4 en longueur. Réalisable aussi la couronne rectangulaire de 1 d'épaisseur, 9 de long et 3 de large; le trou intérieur étant de 7 x 3 x 1. Cube de Soma Inventé par Piet Hein. Le but est de réaliser un cube 3 x 3 x 3 avec 7 pièces: 6 pièces formées de 4 petits cubes; 1 pièce formée de 3 petits cubes. Il y a 230 solutions.

Suite	Pentaminos et grille de jeu (Tectonic) Polyominos Diagrammes de Ferrers Énigmes et jeux – Index
Voir	Carrés parfaits Couverture de l'échiquier Dissections Échecs Lettres de l'alphabet Tangram Stomachion
Site	Les pentaminos
Cette page	http://villemin.gerard.free.fr/Puzzle/minoPent.htm