NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/10/2015 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Outils mathématiques
Débutants Logique	LOGIQUE			Glossaire Logique
INDEX Accueil Sommaire Logique Outils mathématiques	Groupes	Tiers Exclu	Syllogismes	Décision
		Sommaire de cette page >>> Antique >>> Médiéval

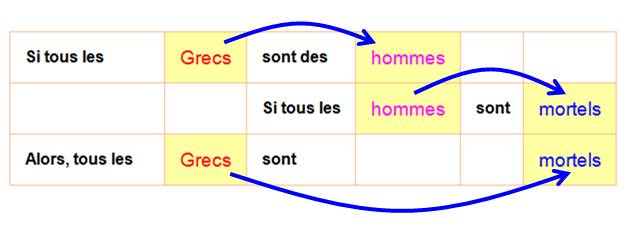
Si A = B et C = B alors A = C.

On sait que si 2 choses sont égales à une troisième,

alors ces deux choses sont égales entre elles

Par exemple

Le mur est jaune. La banane est jaune.

Alors, la banane est mure.

Voir Pensées & humour

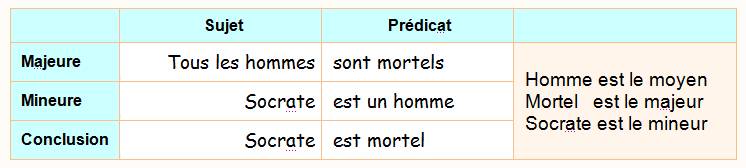
SYLLOGISMES

(un syllogisme)

Étymologie	Du grec sullogismos; de sun, avec, et logos, discours
Définition	Raisonnement qui contient trois propositions la majeure, la mineure et la conclusion et tel que la conclusion est déduite de la majeure par l'intermédiaire de la mineure

Exemple

Majeure Si tous les hommes sont mortels; Mineure Si tous les Grecs sont des hommes; Conclusion Alors, tous les Grecs sont mortels.

ANTIQUE Les cinq formes de raisonnement de Chrysippe (280-204 av. J.-C. )
	Majeure	Mineure	Conclusion
1	Si le premier, le second Si le soleil est là, c'est le jour	Or le premier Le soleil est là	Donc le second C'est le jour
2	Si le premier, le second Si le soleil est là, c'est le jour	Or NON le second Ce n'est pas le jour	Donc NON le premier Le soleil n'est pas là
3	Si NON le premier, et si NON le second, à la fois Les tapis ne sont ni rouges ni brodés (à la fois)	Or le premier Ce tapis est rouge	Donc NON le second Il n'est pas brodé
4	Si ou le premier, ou le second La lampe est éteinte ou allumée	Or le premier La lampe est éteinte	Donc NON le second La lampe n'est pas allumée
5	Si ou le premier, ou le second La lampe est éteinte ou allumée	Or NON le premier La lampe n'est pas éteinte	Donc le second La lampe est allumée

Voir Savants de l'Antiquité

Bilan

Chrysippe dénombre cinq syllogismes de base, indémontrables

Tous les autres syllogismes, plus ou moins complexes, peuvent se ramener à ces cinq de base.

MÉDIÉVAL

Un syllogisme est toujours composé de trois propositions: la majeure, la mineure et la conclusion Chacune de ces propositions est composée d'un sujet et d'un prédicat. Quatre types de propositions de base, chacun codé par une voyelle: Les syllogismes sont construits en associant trois telles propositions. 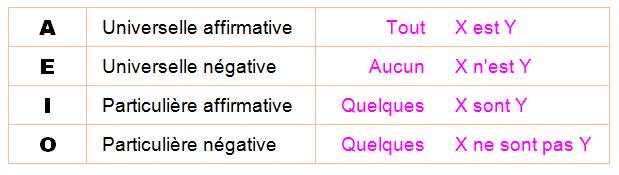Par exemple trois propositions du type A donnent un syllogisme AAA, nommé BARBARA par les logiciens médiévaux: Tout X est Y Or tout Y est Z Donc tout X est Z Ainsi fait, ils distinguent 19 syllogismes: quatre syllogismes de base; - AAA EAE AII EIO quinze syllogismes qui peuvent se ramener à ceux de base. - EAE AEE EIO AOO - AAI EAO IAI AII OAO EIO - AAI AEE IAI EAO EIO Exemple de passage aux syllogismes de base - AEE. - Tout X est Y, or Aucun Z n'est Y, donc Aucun Z n'est X. - Tout X est Y, or Aucun Y n'est Z, donc Aucun X n'est Z. - Aucun Y n'est Z, or Tout X est Y, donc Aucun X n'est Z. - EAE (2^e syllogisme de base).

D'après: Les chemins de la logique – Dossier de Pour la Science de Octobre/décembre 2005

Retour	Tiers Exclu
Suite	Syllogismes – Carte postale Syllogismes et autres types de raisonnements Groupes et nombres Lois de la logique
Voir	Débutants – Index Groupe Jeux et puzzles – Index La logique classique de Boole Les symétries Logique – Index Nombres – Construction des nombres Outils mathématiques – Index Structures algébriques – Index Systèmes experts Théorie des nombres – Index
DicoNombre	Nombre 5
Cette page	http://villemin.gerard.free.fr/Referenc/Outils/AOUTILS/Syllogis.htm