|
|||||||||||||||||||||||||||||||||||
![]()
|
INTRODUCTION
à
la LOGIQUE MATHÉMATIQUE Nous devons d'abord sacrifier à une
formalité: introduire un peu de vocabulaire spécifique à la logique
mathématique. Mots rencontrés dans
cette page
|
|
|
|
|
Proposition La
plage est formée de sable Cette phrase est un énoncé, une
affirmation, une assertion, on dira: une proposition. La
plage de Nice est très jolie cette phrase émet une opinion et n'entre pas
dans la définition d'une proposition telle que nous l'entendons en logique
mathématique. La proposition doit posséder un caractère
de véracité: vrai ou faux; on dira: une valeur
de vérité. La
plage de Ramatuelle (Pampelonne)) est une plage de sable est une
proposition vraie. La
plage de Nice est une plage de sable est une proposition fausse (ce sont des
galets). Une proposition est une affirmation reconnue par tous pour être soit
vraie soit fausse. Voir Tiers exclu Sans autre indication, une proposition
écrite est supposée vraie (par
pure convention). Exemple: p(x)
veut dire que la proposition p(x) est vraie. Voir Différence entre
proposition et assertion Raisonnement
Le raisonnement est un cheminement de pensée qui partant de
propositions en déduit d'autres propositions avec leur valeur de vérité. Logique La logique est la science qui permet d'établir des règles précises
conduisant à un raisonnement
rigoureux. On parle alors de calcul des propositions ou, en
logique avancée (avec introduction de variables), de calcul des prédicats. |
|
Voir Logique des
propositions / Types de
raisonnements
|
|
||||||||||||
|
Petite histoire de logique
Illustration
-
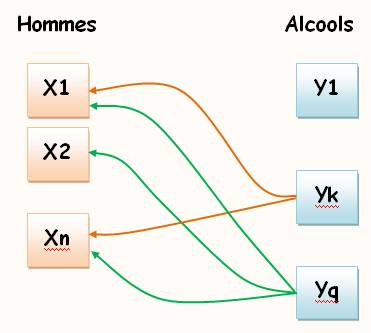
Tous les
éléments de cet ensemble sont des étoiles. -
Il en existe au moins une dont la couleur est noire. Tous pareils: quantificateur
universel
On
lui associe une abréviation:
On peut dire: tous
ou chaque éléments de E. Il existe au moins un: quantificateur
existentiel
On lui associe deux
abréviations selon le cas:
On
peut dire: au moins un ou quelques ou certains
éléments de E. |
||||||||||||
|
|
|
|
X1 est soûl en
buvant Yk Xn se soûle avec Yk
ou Yq
|
|
|
Avec
ce vocabulaire de base, nous
sommes parés pour plonger dans
le bain de la logique mathématique. |
![]()
|
|
||
|
Énoncé |
Phrase qui définit un objet ou en donne les propriétés. Soit x un nombre réel. Le nombre 5 est un nombre entier. |
|
|
Affirmation |
Nom générique d'un énoncé qui peut être vrai, faux, possible,
probable. Affirmation vraie: 1 + 1 = 2. Demain, j'irai faire des course n'est pas une
affirmation (c'est une décision, un souhait, une opinion …) Si elle ne peut être que vraie
ou fausse, c'est une assertion |
|
|
Proposition |
Une proposition est un énoncé que l’on pourra soit démontrer, soit
réfuter: elle est vraie ou fausse. Pour tout Cette carte est un Roi Il pleut. Le sol est mouillé En logique: On parle de logique des propositions. Une proposition est une affirmation à laquelle on peut, sans
ambiguïté, attribuer la valeur vraie ou la valeur fausse. Une proposition satisfait nécessairement les lois suivantes:
|
|
|
Assertion |
Proposition, positive ou négative, que l'on donne comme vraie; sinon
elle fausse. S'il pleut, le sol est mouillé. Si Hollande est hollandais alors 1 + 1 = 3. Si x est inférieur à 100, sa racine est
inférieure à 10. Synonyme en maths de: Hypothèse, Axiome, Postulat ou Conjecture selon
le degré de certitude |
|
|
Prédicat |
Dans "Platon est un homme" Le prédicat est "est un homme". C'est la propriété énoncée En logique avancée, on parle de calcul des prédicats, assertion
dépendant de variables. |
|
|
Alternative |
Une proposition alternative énonce deux choses dont une seule est
vraie. |
|
Voir Théorie, théorèmes et axiomes
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Prof/LOGIQUE/P1intro.htm |
![]()