|
|||||||||||||||||||||||||||||||||||
![]()
|
CRISTAUX Le monde fascinant
et complexe des Symétries.
|
|
|
|
|
Autres?
|
|
|
Angles CONSTANTS
Loi de la forme
primitive: CARACTÉRISTIQUES ENTIÈRES
|
||||||||||||||||
|
|
|
|
|
|

|
|
|||||||||||||||||||||||||||||||||
|
Régularité
Ievgraf Stepanovitch
Fedorov
Auguste Bravais
(1811-1863)
Voici les paramètres
pour les sept mailles
Source image:
Les
sept systèmes cristallins – Mineralogie.fr ce site présente les détails pour chaque systèmes
|
|||||||||||||||||||||||||||||||||
|
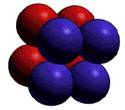
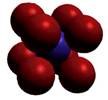
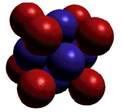
Cubique |
Cubique
centré |
Cubique
à faces centrées |
|
|
|
|
|
|
|||||||||||||||||
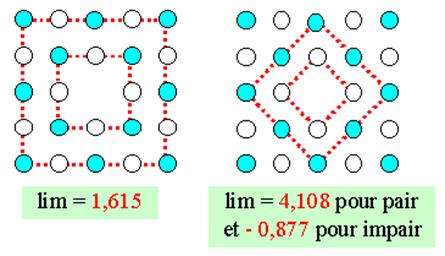
Pour comprendre, plaçons-nous
dans le plan (et
non pas en 3 dimensions):
|
|||||||||||||||||
|
|
|||||||||||
|
Dimensions de la
cellule élémentaire d'un cristal
Dimension du noyau
cristallin
Densité des atomes
dans un cristal
Résistance
électrique
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Ceci
est valable que le tétraèdre soit en
caoutchouc, ou
4 boules retenues par des ressorts
=>
Théorie de la symétrie brisée. |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()
ARCHIVES – Voir explications sur le site de JJ
Chevallier
|
|
||
|
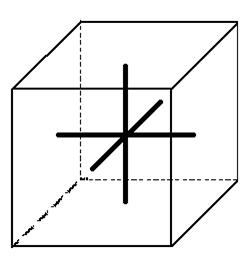
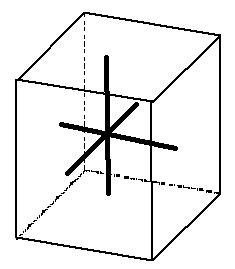
Cubique ou isométrique
|
|
|
|
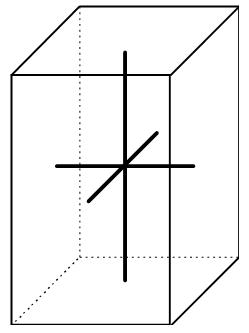
Quadratique ou tétragonal
|
|
|
|
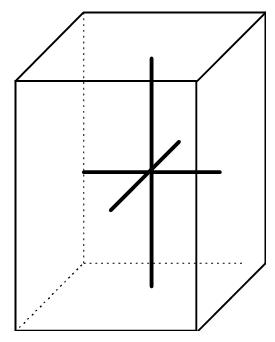
Orthorhombique
|
|
|
|
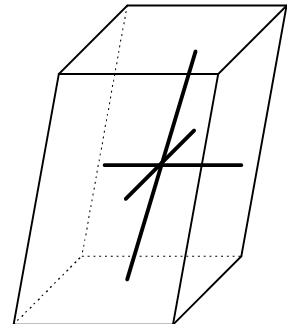
Monoclinique
|
|
|
|
Triclinique
|
|
|
|
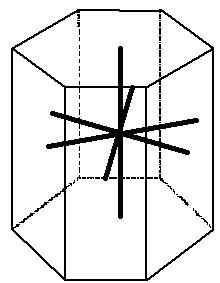
Hexagonal
|
|
|