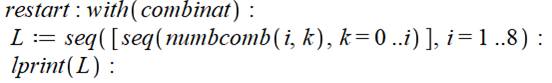NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TABLES
Débutants Général	TRIANGLE de PASCAL	Glossaire Général
INDEX Triangle de Pascal	Sommaire de cette page >>> Liste croissante des coefficients >>> Coefficients en puissance >>> Programmation >>> Table >>> Nombres de Pascal >>> Nombres concaténés premiers

TABLE des coefficients du binôme

ou TRIANGLE de PASCAL

Voir Introduction et développements sur le triangle de Pascal

Anglais: binomial coefficient

Liste des coefficients du binôme jusqu'à 1100

(Liste triée, hors doublons et valeurs triviales)

6, 10, 15, 20, 21, 28, 35, 36, 45, 55, 56, 66, 70, 78, 84, 91, 105, 120, 126, 136, 153, 165, 171, 190, 210, 220, 231, 252, 253, 276, 286, 300, 325, 330, 351, 364, 378, 406, 435, 455, 462, 465, 495, 496, 528, 560, 561, 595, 630, 666, 680, 703, 715, 741, 780, 792, 816, 820, 861, 903, 924, 946, 969, 990, 1001, 1035, 1081 …

Le nombre 1 y est présent une infinité de fois.

Tous les nombres y sont au moins deux fois (dont tous ceux présents au centre d'une ligne et sur les deux bords, hors le 1)

Beaucoup sont présents quatre fois: ceux qui sont symétriques sur une ligne aux bords (hors le 1) et ailleurs, comme le 15 en ligne 15 et en ligne 6.

Le plus petit nombre présent six fois est 120.

Le plus petit nombre présent huit fois est 3 003.

Présents plus de 2 fois jusqu'à 5000 [nombre, quantité]

[6, 3], [10, 4], [15, 4], [20, 3], [21, 4], [28, 4], [35, 4], [36, 4], [45, 4], [55, 4], [56, 4], [66, 4], [70, 3], [78, 4], [84, 4], [91, 4], [105, 4], [120, 6], [126, 4], [136, 4], [153, 4], [165, 4], [171, 4], [190, 4], [210, 6], [220, 4], [231, 4], [252, 3], [253, 4], [276, 4], [286, 4], [300, 4], [325, 4], [330, 4], [351, 4], [364, 4], [378, 4], [406, 4], [435, 4], [455, 4], [462, 4], [465, 4], [495, 4], [496, 4], [528, 4], [560, 4], [561, 4], [595, 4], [630, 4], [666, 4], [680, 4], [703, 4], [715, 4], [741, 4], [780, 4], [792, 4], [816, 4], [820, 4], [861, 4], [903, 4], [924, 3], [946, 4], [969, 4], [990, 4], [1001, 4], [1035, 4], [1081, 4], [1128, 4], [1140, 4], [1176, 4], [1225, 4], [1275, 4], [1287, 4], [1326, 4], [1330, 4], [1365, 4], [1378, 4], [1431, 4], [1485, 4], [1540, 6], [1596, 4], [1653, 4], [1711, 4], [1716, 4], [1770, 4], [1771, 4], [1820, 4], [1830, 4], [1891, 4], [1953, 4], [2002, 4], [2016, 4], [2024, 4], [2080, 4], [2145, 4], [2211, 4], [2278, 4], [2300, 4], [2346, 4], [2380, 4], [2415, 4], [2485, 4], [2556, 4], [2600, 4], [2628, 4], [2701, 4], [2775, 4], [2850, 4], [2925, 4], [2926, 4], [3003, 8], [3060, 4], [3081, 4], [3160, 4], [3240, 4], [3276, 4], [3321, 4], [3403, 4], [3432, 3], [3486, 4], [3570, 4], [3654, 4], [3655, 4], [3741, 4], [3828, 4], [3876, 4], [3916, 4], [4005, 4], [4060, 4], [4095, 4], [4186, 4], [4278, 4], [4368, 4], [4371, 4], [4465, 4], [4495, 4], [4560, 4], [4656, 4], [4753, 4], [4845, 4], [4851, 4], [4950, 4], [4960, 4]

On trouve toutes ces valeurs dans le triangle de Pascal, bords exclus.

Coefficients en puissance

Carrés

k = [2, 9, 50, 289, 1682, 9801, 57122, 332929, …]

k = [2, 3, 4, 50]

Autres

Aucune autre solution. Résultat établit par K. Gyory (1998)

Anglais: find all binomial coefficients which are perfect powers

Voir Factorielles tronquées

Multi-présence

Nombres qui apparaissent plus de quatre fois dans le triangle de Pascal:

1, 120, 210, 1540, 3003, 7140, 11628, 24310, 61218182743304701891431482520, … OEIS A003015

Voir Développements

Programmation Maple
	Commentaires Après initialisation, formation du premier rang du triangle de Pascal et impression. Boucle en i de 2 au rang désirée (ici, 8). Quantité de termes dans la liste en cours en q LL est une liste qui va contenir la liste des nombres de Pascal (p) de rang i, sans les 1 des extrémités. Calcul de ces nombres p par somme deux à deux (boucle en j). Formation de la liste LL en adjoignant p à la liste déjà constituée. La liste finale de rang i est constituée de la liste LL flanquée des deux 1 d'extrémités. Impression de cette liste accompagnée de son rang. En bleu, le résultat du traitement: le triangle de Pascal du rang 1 au rang 8. Traduction de l'anglais restart: redémarrer. lprint: impression (avec l pour linéaire). for … from … to … do: pour … de … à … faire. nops: nombre d'opérateurs (de termes). op pour opérateur d'extraction. od pour do à l'envers soit fin de do (fin de faire).
		On peut aussi calculer directement les coefficients binomiaux disponibles dans le package combinatoire de Maple.

Voir Programmation – Index

Exemples de lecture de la table ci-dessous

Développement de la puissance d'un binôme >>> Ligne 3 => (a + b)^3 = a^3 + 3 a²b + 3 ab² + b^3 Ligne 4 => (a + b)^4 = a^4 + 4 a^3 b + 6 a²b² + 4 ab^3 + b^4 Quantité de combinaisons >>> C7^3 = 35 => il y a 35 combinaisons possibles de 7 objets pris 3 par 3. C7^4 = 35 => il y a 35 combinaisons possibles de 7 objets pris 4 par 4. C20^10 = 184 756 => il y a 184 756 combinaisons possibles de 20 objets pris 10 par 10. C49^6 = 13 983 816 => combinaisons possibles au loto. C49^5 = 1 906 884 => combinaisons possibles pour 5 bons numéros.

Table des coefficients du binôme ou triangle de Pascal

(En nombres en rouge et cases colorées, le ou les deux nombres centraux)

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1	1
2	1	2	1
3	1	3	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1
8	1	8	28	56	70	56	28	8	1
9	1	9	36	84	126	126	84	36	9	1
10	1	10	45	120	210	252	210	120	45	10	1
11	1	11	55	165	330	462	462	330	165	55	11	1
12	1	12	66	220	495	792	924	792	495	220	66	12	1
13	1	13	78	286	715	1 287	1 716	1 716	1 287	715	286	78	13	1
14	1	14	91	364	1 001	2 002	3 003	3 432	3 003	2 002	1 001	364	91	14	1
15	1	15	105	455	1 365	3 003	5 005	6 435	6 435	5 005	3 003	1 365	455	105	15
16	1	16	120	560	1 820	4 368	8 008	11 440	12 870	11 440	8 008	4 368	1 820	560	120
17	1	17	136	680	2 380	6 188	12 376	19 448	24 310	24 310	19 448	12 376	6 188	2 380	680
18	1	18	153	816	3 060	8 568	18 564	31 824	43 758	48 620	43 758	31 824	18 564	8 568	3 060
19	1	19	171	969	3 876	11 628	27 132	50 388	75 582	92 378	92 378	75 582	50 388	27 132	11 628
20	1	20	190	1 140	4 845	15 504	38 760	77 520	125 970	167 960	184 756	167 960	125 970	77 520	38 760
21	1	21	210	1 330	5 985	20 349	54 264	116 280	203 490	293 930	352 716	352 716	293 930	203 490	116 280
22	1	22	231	1 540	7 315	26 334	74 613	170 544	319 770	497 420	646 646	705 432	646 646	497 420	319 770
23	1	23	253	1 771	8 855	33 649	100 947	245 157	490 314	817 190	1 144 066	1 352 078	1 352 078	1 144 066	817 190
24	1	24	276	2 024	10 626	42 504	134 596	346 104	735 471	1 307 504	1 961 256	2 496 144	2 704 156	2 496 144	1 961 256
25	1	25	300	2 300	12 650	53 130	177 100	480 700	1 081 575	2 042 975	3 268 760	4 457 400	5 200 300	5 200 300	4 457 400
26	1	26	325	2 600	14 950	65 780	230 230	657 800	1 562 275	3 124 550	5 311 735	7 726 160	9 657 700	10 400 600	9 657 700
27	1	27	351	2 925	17 550	80 730	296 010	888 030	2 220 075	4 686 825	8 436 285	13 037 895	17 383 860	20 058 300	20 058 300
28	1	28	378	3 276	20 475	98 280	376 740	1 184 040	3 108 105	6 906 900	13 123 110	21 474 180	30 421 755	37 442 160	40 116 600
29	1	29	406	3 654	23 751	118 755	475 020	1 560 780	4 292 145	10 015 005	20 030 010	34 597 290	51 895 935	67 863 915	77 558 760
30	1	30	435	4 060	27 405	142 506	593 775	2 035 800	5 852 925	14 307 150	30 045 015	54 627 300	86 493 225	119 759 850	145 422 675
31	1	31	465	4 495	31 465	169 911	736 281	<<< Non développé >>>
32	1	32	496	4 960	35 960	201 376	906 192
33	1	33	528	5 456	40 920	237 336	1 107 568
34	1	34	561	5 984	46 376	278 256	1 344 904
35	1	35	595	6 545	52 360	324 632	1 623 160
36	1	36	630	7 140	58 905	376 992	1 947 792
37	1	37	666	7 770	66 045	435 897	2 324 784
38	1	38	703	8 436	73 815	501 942	2 760 681
39	1	39	741	9 139	82 251	575 757	3 262 623
40	1	40	780	9 880	91 390	658 008	3 838 380
41	1	41	820	10 660	101 270	749 398	4 496 388
42	1	42	861	11 480	111 930	850 668	5 245 786
43	1	43	903	12 341	123 410	962 598	6 096 454
44	1	44	946	13 244	135 751	1 086 008	7 059 052
45	1	45	990	14 190	148 995	1 221 759	8 145 060
46	1	46	1 035	15 180	163 185	1 370 754	9 366 819
47	1	47	1 081	16 215	178 365	1 533 939	10 737 573
48	1	48	1 128	17 296	194 580	1 712 304	12 271 512
49	1	49	1 176	18 424	211 876	1 906 884	13 983 816
50	1	50	1 225	19 600	230 300	2 118 760	15 890 700

Voir Calculs sur les combinaisons

Mille et une façons de faire des combinaisons: 1001, 2002, …

La suite de ces nombres par ordre croissant:

1001, 2002, 3003, 5005, 8008, 41041, 66066, 76076, 79079, 203203, 230230, 255255, 426426,

500500, 501501, 581581, 620620, 646646, 720720, 828828, 930930930930 …

Voir Nombre 1001 / Combinaisons / Coefficients du binôme / Mille et une manières

Notes

Un nombre est la somme de tous ceux qui sont au-dessus, sur la colonne précédente (à gauche) Chaque colonne représente la suite de nombres géométriques de dimensions successives (2D, 3D, 4D …)
Colonne 2 2D Nombres triangulaires	Colonne 3 3D Nombres tétraédriques	Colonne 4 4D Nombres pentatopes

Nombres de Pascal jusqu'à 5 000

Rang, colonne, nombre de Pascal

Exception des nombres triviaux comme le 1 et les nombres entiers successifs de la colonne 1.

1 2 6 2 2 10 3 2 15 4 3 20 5 2 21 6 2 28 7 3 35 8 2 36 9 2 45 10 2 55 11 3 56 12 2 66 13 4 70 14 2 78 15 3 84 16 2 91 17 2 105 18 2 120 19 3 120 20 4 126 21 2 136 22 2 153 23 3 165 24 2 171 25 2 190 26 2 210 27 4 210 28 3 220 29 2 231 30 5 252 31 2 253 32 2 276 33 3 286 34 2 300 35 2 325 36 4 330 37 2 351 38 3 364 39 2 378 40 2 406 41 2 435 42 3 455 43 5 462 44 2 465 45 4 495 46 2 496 47 2 528 48 3 560 49 2 561 50 2 595 51 2 630 52 2 666 53 3 680 54 2 703 55 4 715 56 2 741 57 2 780 58 5 792 59 3 816 60 2 820 61 2 861 62 2 903 63 6 924 64 2 946 65 3 969 66 2 990 67 4 1 001 68 2 1 035 69 2 1 081 70 2 1 128 71 3 1 140 72 2 1 176 73 2 1 225 74 2 1 275

75 5 1 287 76 2 1 326 77 3 1 330 78 4 1 365 79 2 1 378 80 2 1 431 81 2 1 485 82 2 1 540 83 3 1 540 84 2 1 596 85 2 1 653 86 2 1 711 87 6 1 716 88 2 1 770 89 3 1 771 90 4 1 820 91 2 1 830 92 2 1 891 93 2 1 953 94 5 2 002 95 2 2 016 96 3 2 024 97 2 2 080 98 2 2 145 99 2 2 211 100 2 2 278 101 3 2 300 102 2 2 346 103 4 2 380 104 2 2 415 105 2 2 485 106 2 2 556 107 3 2 600 108 2 2 628 109 2 2 701 110 2 2 775 111 2 2 850 112 3 2 925 113 2 2 926 114 2 3 003 115 5 3 003 116 6 3 003 117 4 3 060 118 2 3 081 119 2 3 160 120 2 3 240 121 3 3 276 122 2 3 321 123 2 3 403 124 7 3 432 125 2 3 486 126 2 3 570 127 3 3 654 128 2 3 655 129 2 3 741 130 2 3 828 131 4 3 876 132 2 3 916 133 2 4 005 134 3 4 060 135 2 4 095 136 2 4 186 137 2 4 278 138 5 4 368 139 2 4 371 140 2 4 465 141 3 4 495 142 2 4 560 143 2 4 656 144 2 4 753 145 4 4 845 146 2 4 851 147 2 4 950 148 3 4 960

Les nombres de Pascal concaténés sont-ils premiers?

Les nombres d'une même ligne sont collés ensemble (concaténés)

1 11 PREMIER

2 121 composé

3 1331 composé

4 14641 composé

5 15101051 composé

6 1615201561 composé

7 172135352171 composé

8 18285670562881 PREMIER

9 193684126126843691 composé

10 1104512021025221012045101 composé

11 1115516533046246233016555111 composé

12 1126622049579292479249522066121 composé

13 11378286715128717161716128771528678131 composé

14 11491364100120023003343230032002100136491141 composé

15 11510545513653003500564356435500530031365455105151 composé

16 116120560182043688008114401287011440800843681820560120161 composé

17 1171366802380618812376194482431024310194481237661882380680136171 composé

18 118153816306085681856431824437584862043758318241856485683060816153181 composé

19 1191719693876116282713250388755829237892378755825038827132116283876969171191 composé

20 1201901140484515504387607752012597016796018475616796012597077520387601550448451140190201 composé

Voir	Triangle de Pascal Divisibilité des coefficients du triangle Identités Binôme de Newton Nombres géométriques Nombres géométriques – Tables
DicoNombre	Nombre 140 Nombre 9 801
Site	A007318 – Pascal's triangle read by rows: A006987 – Binomial coefficients: C(n,k), 2 <= k <= n-2, sorted, duplicates removed. Power values of binomial coefficients – K. Gyory
Cette page	http://villemin.gerard.free.fr/TABLES/Pascal.htm