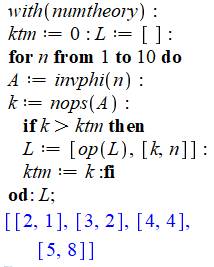|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Fonction PHI d'EULER ou indicatrice d'EULER ou totient d'EULER Table jusqu'à Phi = 500 Phi (n) est la quantité de nombres premiers avec n,
inférieurs à n. |
|
|
|
|
Nombres
en tant que totient des nombres indiqués 1, [1, 2], 2 2, [3, 4, 6], 3 4, [5, 8, 10, 12], 4 6, [7, 9, 14, 18],
4 Exemple: il ya quatre
nombres dont le totient est 6 8, [15, 16, 20, 24, 30], 5 10, [11, 22], 2 12, [13, 21, 26, 28, 36, 42], 6 16, [17, 32, 34,
40, 48, 60], 6 18, [19, 27, 38,
54], 4 20, [25, 33, 44,
50, 66], 5 22, [23, 46], 2 24, [35, 39, 45, 52, 56, 70, 72,
78, 84, 90], 10 28, [29, 58], 2 30, [31, 62], 2 32, [51, 64, 68,
80, 96, 102, 120], 7 36, [37, 57, 63,
74, 76, 108, 114, 126], 8 40, [41, 55, 75,
82, 88, 100, 110, 132, 150], 9 42, [43, 49, 86,
98], 4 44, [69, 92, 138],
3 46, [47, 94], 2 48, [65, 104, 105, 112, 130, 140,
144, 156, 168, 180, 210], 11 52, [53, 106], 2 54, [81, 162], 2 56, [87, 116, 174],
3 58, [59, 118], 2 60, [61, 77, 93,
99, 122, 124, 154, 186, 198], 9 64, [85, 128, 136,
160, 170, 192, 204, 240], 8 66, [67, 134], 2 70, [71, 142], 2 72, [73, 91, 95, 111, 117, 135,
146, 148, 152, 182, 190, 216, 222, 228, 234, 252, 270], 17 78, [79, 158], 2 80, [123, 164, 165,
176, 200, 220, 246, 264, 300, 330], 10 82, [83, 166], 2 84, [129, 147, 172,
196, 258, 294], 6 88, [89, 115, 178,
184, 230, 276], 6 92, [141, 188,
282], 3 96, [97, 119, 153,
194, 195, 208, 224, 238, 260, 280, 288, 306, 312, 336, 360, 390, 420], 17 100, [101, 125, 202, 250], 4 Nombres
hautement totient (reprend
les totients des lignes en jaune) [[1, 2], [2, 3], [4, 4], [8, 5],
[12, 6], [24, 10], [48, 11], [72, 17], [144, 21], [240, 31], [432,
34], [480, 37], [576, 38], [720, 49], [1152, 54], [1440, 72]] >>> |
|
|
Nombres
n et n + 1 tel que phi(n) = phi(n + 1).
Liste jusqu'à un million 1,
3, 15, 104, 164, 194, 255, 495, 584, 975, 2204, 2625, 2834, 3255, 3705, 5186,
5187, 10604, 11715, 13365, 18315, 22935, 25545, 32864, 38804, 39524, 46215,
48704, 49215, 49335, 56864, 57584, 57645, 64004, 65535, 73124, 105524,
107864, 123824, 131144, 164175, 184635, 198315, 214334, 215775, 256274,
286995, 307395, 319275, 347324, 388245, 397485, 407924, 415275, 454124,
491535, 524432, 525986, 546272, 568815, 589407, 679496, 686985, 840255,
914175, 936494, 952575, 983775 |
|
|
|
|
Lecture de la table
Rappel : tous les nombres
impairs sont non-totient. |
|
|
|
Voici,
les instructions Maple à
utiliser. D'abord,
faire appel au package de la théorie des nombres. phi(n) délivre
directement le totient de t. invphi(t) donne tous les
nombres n ayant pour totient t. |
Voir Programmation – Index
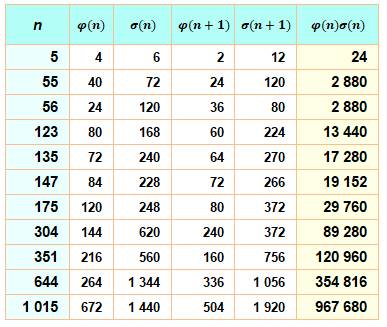
Produit du totient par la somme des
diviseurs de deux nombres voisins
|
Exemple
Notez le triplet avec 55, 56 et 57 Voir Somme
des diviseurs (sigma). |
|
Cas où le produit
du totient par sigma
est un carré, jusqu'à 1000: [n, sigma.phi, sa racine carrée] [1,
1, 1], [14, 144, 12], [30, 576, 24], [51, 2304, 48], [105, 9216, 96], [170,
20736, 144], [194, 28224, 168], [248, 57600, 240], [264, 57600, 240], [364,
112896, 336], [405, 156816, 396], [418, 129600, 360], [477, 219024, 468],
[595, 331776, 576], [679, 451584, 672], [714, 331776, 576], [760, 518400,
720], [780, 451584, 672] Cas où le produit du totient par tau
est un carré, jusqu'à 1000: [n, tau.phi, sa racine carrée] [1,
1, 1], [7, 16, 4], [17, 36, 6], [22, 144, 12], [30, 576, 24], [31, 64, 8],
[71, 144, 12], [94, 576, 24], [97, 196, 14], [115, 576, 24], [119, 576, 24],
[127, 256, 16], [138, 2304, 48], [154, 2304, 48], [164, 1764, 42], [165,
2304, 48], [199, 400, 20], [210, 9216, 96], [214, 1296, 36], [217, 1024, 32],
[232, 3600, 60], [241, 484, 22], [260, 7056, 84], [265, 1296, 36], [318,
5184, 72], [337, 676, 26], [343, 1600, 40], [374, 5184, 72], [382, 2304, 48],
[449, 900, 30], [497, 2304, 48], [510, 20736, 144] Cas où le totient est égal au carré du produit des facteurs 1, 8, 108, 250, 6 174, 51 154. FIN |
|
Nombres
tels que leur totient est inférieur au totient du nombre suivant, lequel est
inférieur au nombre qui suit …
Trois totients croissants 105,
165, 315, 525, 585, 735, 1155, 1365, 1484, 1485, 1575, 1755, 1785, 1815,
1995, … Exemple: Quatre totients croissants 1484,
2534, 3002, 3674, 3926, 4454, 4484, 4784, 4844, 5264, 5312, … Cinq totients croissants Aucun
jusqu'à un million. Pourtant, on pense qu'ils sont en quantité infinie quelle
que soit k, la quantité d'inégalités. |
![]()
|
|
|
|
0,
=> 1, par convention 2,
=> 3, 4, 6 4,
=> 5, 8, 10, 12 6, => 7, 9, 14, 18 8,
=> 15, 16, 20, 24, 30 10,
=> 11, 22 12,
=> 13, 21, 26, 28, 36, 42 14, NON-TOTIENT 16,
=> 17, 32, 34, 40, 48, 60 18,
=> 19, 27, 38, 54 20,
=> 25, 33, 44, 50, 66 22,
=> 23, 46 24,
=> 35, 39, 45, 52, 56, 70,
72, 78, 84, 90 26, NON-TOTIENT 28,
=> 29, 58 30,
=> 31, 62 32,
=> 51, 64, 68, 80, 96, 102,
120 34, NON-TOTIENT 36,
=> 37, 57, 63, 74, 76, 108,
114, 126 38, NON-TOTIENT 40,
=> 41, 55, 75, 82, 88, 100,
110, 132, 150 42,
=> 43, 49, 86, 98 44,
=> 69, 92, 138 46,
=> 47, 94 48,
=> 65, 104, 105, 112, 130,
140, 144, 156, 168, 180, 210 50, NON-TOTIENT 52,
=> 53, 106 54,
=> 81, 162 56,
=> 87, 116, 174 58,
=> 59, 118 60,
=> 61, 77, 93, 99, 122, 124,
154, 186, 198 62, NON-TOTIENT 64,
=> 85, 128, 136, 160, 170,
192, 204, 240 66,
=> 67, 134 68, NON-TOTIENT 70,
=> 71, 142 72,
=> 73, 91, 95, 111, 117,
135, 146, 148, 152, 182, 190, 216, 222, 228, 234, 252, 270 74, NON-TOTIENT 76, NON-TOTIENT 78,
=> 79, 158 80,
=> 123, 164, 165, 176, 200,
220, 246, 264, 300, 330 82,
=> 83, 166 84,
=> 129, 147, 172, 196, 258,
294 86, NON-TOTIENT 88,
=> 89, 115, 178, 184, 230,
276 90, NON-TOTIENT 92,
=> 141, 188, 282 94, NON-TOTIENT 96,
=> 97, 119, 153, 194, 195,
208, 224, 238, 260, 280, 288, 306, 312, 336, 360, 390, 420 98, NON-TOTIENT 100,
=> 101, 125, 202, 250 |
|
|
|
|
|
100,
=> 101, 125, 202, 250 102,
=> 103, 206 104,
=> 159, 212, 318 106,
=> 107, 214 108,
=> 109, 133, 171, 189, 218,
266, 324, 342, 378 110,
=> 121, 242 112,
=> 113, 145, 226, 232, 290,
348 114, NON-TOTIENT 116,
=> 177, 236, 354 118, NON-TOTIENT 120,
=> 143, 155, 175, 183, 225,
231, 244, 248, 286, 308, 310, 350, 366, 372, 396, 450, 462 122, NON-TOTIENT 124, NON-TOTIENT 126,
=> 127, 254 128,
=> 255, 256, 272, 320, 340, 384,
408, 480, 510 130,
=> 131, 262 132,
=> 161, 201, 207, 268, 322,
402, 414 134, NON-TOTIENT 136,
=> 137, 274 138,
=> 139, 278 140,
=> 213, 284, 426 142, NON-TOTIENT 144,
=> 185, 219, 273, 285, 292,
296, 304, 315, 364, 370, 380, 432, 438, 444, 456, 468, 504, 540, 546, 570,
630 146, NON-TOTIENT 148,
=> 149, 298 150,
=> 151, 302 152, NON-TOTIENT 154, NON-TOTIENT 156,
=> 157, 169, 237, 314, 316,
338, 474 158, NON-TOTIENT 160,
=> 187, 205, 328, 352, 374,
400, 410, 440, 492, 528, 600, 660 162,
=> 163, 243, 326, 486 164,
=> 249, 332, 498 166,
=> 167, 334 168,
=> 203, 215, 245, 261, 344,
392, 406, 430, 490, 516, 522, 588 170, NON-TOTIENT 172,
=> 173, 346 174, NON-TOTIENT 176,
=> 267, 345, 356, 368, 460,
534, 552, 690 178,
=> 179, 358 180,
=> 181, 209, 217, 279, 297,
362, 418, 434, 558, 594 182, NON-TOTIENT 184,
=> 235, 376, 470, 564 186, NON-TOTIENT 188, NON-TOTIENT 190,
=> 191, 382 192,
=> 193, 221, 291, 357, 386, 388,
416, 442, 448, 476, 520, 560, 576, 582, 612, 624, 672, 714, 720, 780, 840 194, NON-TOTIENT 196,
=> 197, 394 198,
=> 199, 398 200,
=> 275, 303, 375, 404, 500,
550, 606, 750 202, NON-TOTIENT 204,
=> 309, 412, 618 206, NON-TOTIENT 208,
=> 265, 424, 530, 636 210,
=> 211, 422 212,
=> 321, 428, 642 214, NON-TOTIENT 216,
=> 247, 259, 327, 333, 351,
399, 405, 436, 494, 518, 532, 648, 654, 666, 684, 702, 756, 798, 810 218, NON-TOTIENT 220,
=> 253, 363, 484, 506, 726 222,
=> 223, 446 224,
=> 339, 435, 452, 464, 580,
678, 696, 870 226,
=> 227, 454 228,
=> 229, 458 230, NON-TOTIENT 232,
=> 233, 295, 466, 472, 590,
708 234, NON-TOTIENT 236, NON-TOTIENT 238,
=> 239, 478 240,
=> 241, 287, 305, 325, 369, 385,
429, 465, 482, 488, 495, 496, 525, 572, 574, 610, 616, 620, 650, 700, 732,
738, 744, 770, 792, 858, 900, 924, 930, 990, 1050 242, NON-TOTIENT 244, NON-TOTIENT 246, NON-TOTIENT 248, NON-TOTIENT 250,
=> 251, 502 252,
=> 301, 381, 387, 441, 508,
602, 762, 774, 882 254, NON-TOTIENT 256,
=> 257, 512, 514, 544, 640,
680, 768, 816, 960, 1020 258, NON-TOTIENT 260,
=> 393, 524, 786 262,
=> 263, 526 264,
=> 299, 335, 483, 536, 598,
644, 670, 804, 828, 966 266, NON-TOTIENT 268,
=> 269, 538 270,
=> 271, 542 272,
=> 289, 411, 548, 578, 822 274, NON-TOTIENT 276,
=> 277, 329, 417, 423, 554,
556, 658, 834, 846 278, NON-TOTIENT 280,
=> 281, 319, 355, 562, 568,
638, 710, 852 282,
=> 283, 566 284, NON-TOTIENT 286, NON-TOTIENT 288,
=> 323, 365, 455, 459, 555,
584, 585, 592, 608, 646, 728, 730, 740, 760, 864, 876, 888, 910, 912, 918,
936, 1008, 1080, 1092, 1110, 1140, 1170, 1260 290, NON-TOTIENT 292,
=> 293, 586 294,
=> 343, 686 296,
=> 447, 596, 894 298, NON-TOTIENT 300,
=> 341, 453, 604, 682, 906 302, NON-TOTIENT 304, NON-TOTIENT 306,
=> 307, 614 308, NON-TOTIENT 310,
=> 311, 622 312,
=> 313, 371, 395, 471, 477,
507, 626, 628, 632, 676, 742, 790, 942, 948, 954, 1014 314, NON-TOTIENT 316,
=> 317, 634 318, NON-TOTIENT 320,
=> 425, 561, 615, 656, 704,
748, 800, 820, 850, 880, 984, 1056, 1122, 1200, 1230, 1320 322, NON-TOTIENT 324,
=> 489, 513, 567, 652, 972,
978, 1026, 1134 326, NON-TOTIENT 328,
=> 415, 664, 830, 996 330,
=> 331, 662 332,
=> 501, 668, 1002 334, NON-TOTIENT 336,
=> 337, 377, 609, 645, 674,
688, 735, 754, 784, 812, 860, 980, 1032, 1044, 1176, 1218, 1290, 1470 338, NON-TOTIENT 340, NON-TOTIENT 342,
=> 361, 722 344,
=> 519, 692, 1038 346,
=> 347, 694 348,
=> 349, 413, 531, 698, 826,
1062 350, NON-TOTIENT 352,
=> 353, 391, 445, 706, 712,
736, 782, 890, 920, 1068, 1104, 1380 354, NON-TOTIENT 356,
=> 537, 716, 1074 358,
=> 359, 718 360,
=> 403, 407, 427, 475, 543, 549,
627, 651, 675, 693, 724, 806, 814, 836, 854, 868, 950, 1086, 1098, 1116,
1188, 1254, 1302, 1350, 1386 362, NON-TOTIENT 364, NON-TOTIENT 366,
=> 367, 734 368,
=> 705, 752, 940, 1128, 1410 370, NON-TOTIENT 372,
=> 373, 746 374, NON-TOTIENT 376, NON-TOTIENT 378,
=> 379, 758 380,
=> 573, 764, 1146 382,
=> 383, 766 384,
=> 485, 579, 595, 663, 765,
772, 776, 832, 884, 896, 952, 970, 1040, 1120, 1152, 1158, 1164, 1190, 1224,
1248, 1326, 1344, 1428, 1440, 1530, 1560, 1680 386, NON-TOTIENT 388,
=> 389, 778 390, NON-TOTIENT 392,
=> 591, 788, 1182 394, NON-TOTIENT 396,
=> 397, 437, 469, 597, 603,
621, 794, 796, 874, 938, 1194, 1206, 1242 398, NON-TOTIENT 400,
=> 401, 451, 505, 802, 808,
825, 902, 1000, 1010, 1100, 1212, 1500, 1650 402, NON-TOTIENT 404, NON-TOTIENT 406, NON-TOTIENT 408,
=> 409, 515, 818, 824, 1030,
1236 410, NON-TOTIENT 412, NON-TOTIENT 414, NON-TOTIENT 416,
=> 795, 848, 1060, 1272,
1590 418,
=> 419, 838 420,
=> 421, 473, 497, 539, 633, 639,
842, 844, 946, 994, 1078, 1266, 1278 422, NON-TOTIENT 424,
=> 535, 856, 1070, 1284 426, NON-TOTIENT 428, NON-TOTIENT 430,
=> 431, 862 432,
=> 433, 481, 511, 545, 657,
665, 741, 777, 819, 855, 866, 872, 945, 962, 988, 1022, 1036, 1064, 1090, 1296,
1308, 1314, 1330, 1332, 1368, 1404, 1482, 1512, 1554, 1596, 1620, 1638, 1710,
1890 434, NON-TOTIENT 436, NON-TOTIENT 438,
=> 439, 878 440,
=> 575, 605, 759, 968, 1012,
1150, 1210, 1452, 1518 442,
=> 443, 886 444,
=> 669, 892, 1338 446, NON-TOTIENT 448,
=> 449, 493, 565, 898, 904,
928, 986, 1130, 1160, 1356, 1392, 1740 450, NON-TOTIENT 452,
=> 681, 908, 1362 454, NON-TOTIENT 456,
=> 457, 687, 914, 916, 1374 458, NON-TOTIENT 460,
=> 461, 517, 922, 1034 462,
=> 463, 926 464,
=> 699, 885, 932, 944, 1180,
1398, 1416, 1770 466,
=> 467, 934 468,
=> 553, 711, 1106, 1422 470, NON-TOTIENT 472, NON-TOTIENT 474, NON-TOTIENT 476,
=> 717, 956, 1434 478,
=> 479, 958 480,
=> 527, 533, 715, 723, 861,
915, 964, 975, 976, 992, 1054, 1066, 1144, 1148, 1155, 1220, 1232, 1240,
1300, 1400, 1430, 1446, 1464, 1476, 1488, 1540, 1584, 1716, 1722, 1800, 1830,
1848, 1860, 1950, 1980, 2100, 2310 482, NON-TOTIENT 484, NON-TOTIENT 486,
=> 487, 729, 974, 1458 488, NON-TOTIENT 490,
=> 491, 982 492,
=> 581, 747, 1162, 1494 494, NON-TOTIENT 496, NON-TOTIENT 498,
=> 499, 998 500,
=> 625, 753, 1004, 1250,
1506 |
|
Mêmes chiffres pour le nombre et son totient
|
Nombres
dont le totient a les mêmes chiffres que lui. Liste avec nombre suivi de son totient [1,
1], [21, 12], [63, 36], [291, 192], [502, 250], [2518, 1258], [2817, 1872], [2991,
1992], [4435, 3544], [5229, 2952], [5367, 3576], [5637, 3756], [6102, 2016],
[6174, 1764], [6543, 4356], [6822, 2268], [7236, 2376], [7422, 2472], [8022,
2280], [8541, 5184], [8982, 2988], … |
![]()
|
ou fortement totient (highly totient number) |
|
||||||||||||||||||||||||||||||||||||
|
Définition Nombre k
qui est le totient de plus en plus de nombres, un record. La suite
de ces nombres commencent par 1, 2, 4, 8 … (Tableau) pour des records de quantité de 2, 3, 4, 5 Propriétés Comme
pour les nombres hautement
composés, hormis le premier, tous les autres sont pairs. Ils sont
en quantité infinie. |
Exemples
|
||||||||||||||||||||||||||||||||||||
|
Programme Maple
|
Commentaires Utilisation des logiciels de théorie des nombres. Compteur de records en ktm et préparation de la
liste L des nombres hautement indicateurs. Boucle d'exploration en n. Pour chaque n, liste des nombres ayant ce totient
en A. O s'intéresse à la quantité d'éléments dans la liste q. Chaque que q dépasse le record en cours (ktm),
mise en liste de ce totient k et du nombre n associé. Résultat de l'exécution en bleu. |
Liste [Qté, k hautement indicateur] [2, 1], [3, 2], [4, 4], [5, 8], [6, 12], [10,
24], [11, 48], [17, 72], [21, 144], [31, 240], [34, 432], [37, 480], [38,
576], [49, 720], [54, 1152], [72, 1440], [98, 2880], [126, 4320], [129,
5760], [176, 8640], [178, 11520], [247, 17280], [276, 25920], [281, 30240], [331, 34560],
[359, 40320], [399, 51840], [441, 60480], [454, 69120], [525, 80640] … |
|||||||||||||||||||||||||||||||||||
Voir Programmation – Index
|
|
||
|
Quels
sont les nombres dont le totient est un multiple du nombre consécutif suivant
? Exemple
Liste pour n jusqu'à 10 000 On donne la valeur de n est la valeur k du
rapport entre phi(n) et phi(n+1). Pour 629, on trouve [629, 4]. k = 4 pour 629, 1 469, 85 139, 100
889, 139 859, 154 979, 168 149, 304 079, 396 899, 838 199, … Records 11, 52, 1193, 6294,
17 907 1195 |
[1, 1], [3, 1], [5, 2], [13, 2], [15, 1], [35,
2], [37, 2], [61, 2], [73, 2], [104, 1], [119, 3], [157, 2], [164, 1], [193,
2], [194, 1], [255, 1], [277, 2], [313, 2], [397, 2], [421, 2], [455, 2],
[457, 2], [495, 1], [527, 3], [541, 2], [545, 3], [584, 1], [613, 2], [629, 4], [661, 2], [665, 2], [673, 2], [733, 2],
[757, 2], [877, 2], [975, 1], [997, 2], [1085, 2], [1093, 2], [1153, 2],
[1201, 2], [1213, 2], [1237, 2], [1295, 2], [1321, 2], [1381, 2], [1453, 2],
[1469, 4], [1621, 2], [1657, 2], [1753, 2],
[1873, 2], [1933, 2], [1993, 2], [2017, 2], [2137, 2], [2169, 2], [2204, 1],
[2341, 2], [2473, 2], [2557, 2], [2593, 2], [2625, 1], [2797, 2], [2834, 1],
[2849, 3], [2857, 2], [2917, 2], [2975, 2], [3061, 2], [3217, 2], [3253, 2],
[3255, 1], [3313, 2], [3517, 2], [3689, 3], [3705, 1], [3733, 2], [4021, 2],
[4057, 2], [4177, 2], [4261, 2], [4273, 2], [4357, 2], [4441, 2], [4487, 3],
[4561, 2], [4621, 2], [4879, 2], [4933, 2], [5077, 2], [5101, 2], [5113, 2],
[5186, 1], [5187, 1], [5233, 2], [5413, 2], [5437, 2], [5581, 2], [5701, 2],
[6037, 2], [6073, 2], [6121, 2], [6133, 2], [6217, 2], [6337, 2], [6361, 2],
[6373, 2], [6637, 2], [6649, 3], [6661, 2], [6781, 2], [6997, 2], [7057, 2],
[7213, 2], [7393, 2], [7417, 2], [7477, 2], [7537, 2], [7595, 2], [7753, 2],
[7933, 2], [8053, 2], [8101, 2], [8221, 2], [8317, 2], [8353, 2], [8461, 2],
[8521, 2], [8677, 2], [8713, 2], [8893, 2], [9013, 2], [9133, 2], [9181, 2],
[9241, 2], [9277, 2], [9601, 2], [9661, 2], [9721, 2], [9817, 2], [9901, 2],
[9973, 2] |
|
|
Quels sont
les nombres dont le totient du suivant est un multiple du totient du nombre ? Exemple
Pas de rapport 4 Testé jusqu'à 1 000 000 |
[1, 1], [2, 2], [3, 1], [4, 2], [6, 3], [12, 3],
[15, 1], [16, 2], [18, 3], [36, 3], [72, 3], [90, 3], [96, 3], [104, 1], [108, 3], [154, 2], [162, 3], [164, 1], [192, 3],
[194, 1], [255, 1], [256, 2], [286, 2], [364, 2], [432, 3], [486, 3], [495,
1], [576, 3], [584, 1], [702, 3], [768, 3], [792, 3], [804, 2], [924, 3],
[975, 1], [1066, 2], [1152, 3], [1260, 4], [1296, 3], [1458, 3], [2146, 2],
[2204, 1], [2592, 3], [2625, 1], [2834, 1], [2916, 3], [3255, 1], [3382, 2],
[3456, 3], [3705, 1], [3888, 3], [4550, 2], [4698, 3], [5186, 1], [5187, 1],
[5550, 3], [6106, 2], [6696, 3], [7700, 2], [7998, 3], [8176, 2], [8700, 3],
[9268, 2] |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()