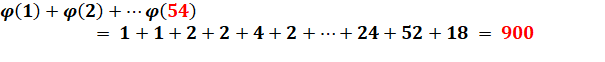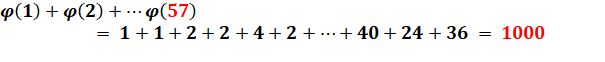|
|||||||||||||||||||||||||||||||||||||||
![]()
|
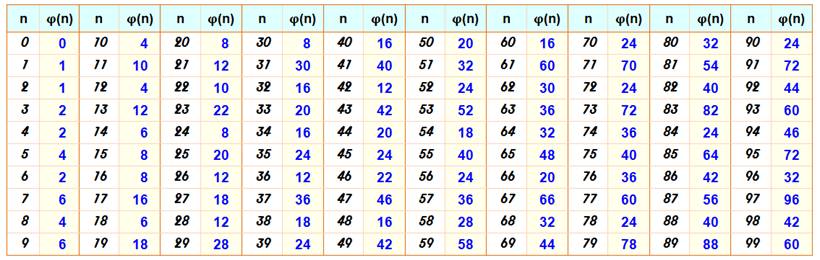
Fonction PHI d'EULER ou indicatrice d'EULER ou totient d'EULER Approche et Valeurs Phi (n) est la quantité de nombres
premiers avec n,
inférieurs à n. C'est aussi la manière de compter une quantité de fractions. Une manière de partager les
nombres en deux catégories: totients et
non-totients. Exemples
Le totient d'un nombre premier p est égal à p –
1; car il est premier avec tous ses prédécesseurs. Le cototient
est le complémentaire du totient, le nombre étant compté. Le cototient de 12
est 8 (7 "trous" + le nombre 12).
|
Voir approche simple en Débutants
Indicatrice ou totient
|
L'un
est plus en usage en français (indicatrice); l'autre est le nom que lui donne
les anglo-saxons: totient. Totient
vient du latin: totiens qui
signifie autant de fois, tant de fois;
totiens … quotiens: autant de fois
… que. |
Ne pas confondre
|
Phi(n)
= Quantité de nombres premiers avec n et inférieurs à n. Pi(n)
= Quantité de nombre premiers inférieurs à n. |
|
|
||||
|
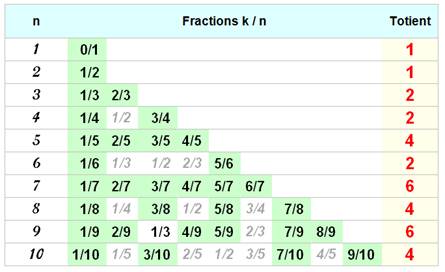
Soit n et toutes les fractions en avec k = 1 à n |
|
|||
|
Le nombre donnant la quantité de fractions qui ne se
simplifient pas - qui nécessitent le dénominateur n - est appelé
totient ou indicatrice d'Euler (Phi de n). |
|
|||
|
Exemple pour n
de 1 à 10 |
|
|||
|
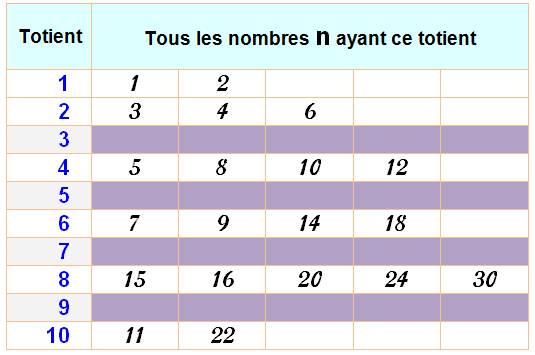
Propriété Tout totient se retrouve au moins deux fois. Non
démontré, mais valable au moins pour n < 1010 000 Suite >>> |
Pour 100 Il faut que le numérateur soit impair et parmi ceux qui
restent (1, 3, 5, 7, 9), en fait, 4 sur 5 ne permettrons pas la
simplification
Suite
(Calcul) >>> |
|||
Cototient: un facteur en commun
|
Cototient:
quantité d'entiers positifs inférieurs à n
qui ont au moins un facteur premier en commun avec n. Il est
égal à n- |
|
|
||
|
Avec l'approche par les fractions, nous pouvons
illustrer ce théorème: Tout nombre est égal à la somme des totients de ses diviseurs |
|
|
|
|
|
|
Voir Table des totients jusqu'à 500 Aucun nombre n'a pour totient 3, 5, 9 … 2k + 1
… Ce sont des Non-totients 24 est le totient de 10 nombres 72 est le totient de 17 nombres {73, 91, 95, 111, 117,
135, 146, 148, 152, 182, 190, 216, 222, 228, 234, 252, 270} Le totient d'un semi premier pq est simplement
calculé par φ(n) = n + 1 − (p + q)
|
|
Enchainement des totients de 2 à 100
Exemple de lecture: 85
a pour totient 64, lequel a 32, lequel a 16, puis 8, 4, 2 (soit un cycle de
longueur 7)

|
|
||
|
On considère un nombre, son totient; le totient de ce
nombre; etc. La liste ci-dessous montre les records
de longueurs de la suite. Exemple: pour 257, il faut
10 chiffres ou 8 étapes pour atteindre le 2 2, [2, 1] 3, [3, 2, 1] 4, [5, 4, 2, 1] 5, [11, 10, 4, 2, 1] 6, [17, 16, 8, 4, 2, 1] 7, [41, 40, 16, 8, 4, 2, 1] 8, [83, 82, 40, 16, 8, 4, 2, 1] 9, [137, 136, 64, 32, 16, 8, 4, 2, 1] 10, [257, 256, 128,
64, 32, 16, 8, 4, 2, 1] 11, [641, 640, 256,
128, 64, 32, 16, 8, 4, 2, 1] 12, [1097, 1096, 544, 256, 128, 64, 32, 16, 8, 4, 2, 1] 13, [2329, 2176,
1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1] 14, [4369, 4096,
2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1] 15, [10537, 10240,
4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1] 16, [17477, 17476,
8192, 4096, 2048, 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1] 17, [35209, 34816,
16384, 8192, …] 18, [65537, 65536,
32768, 16384, …] 19, [140417,
140416, 70144, 34816, 16384, …] 20, [281929, 280576,
139264, 65536, 32768, 16384, …] 21, [557057,
557056, 262144, 131072, 65536, …] 22, [1114129,
1048576, 524288, 262144, 131072, 65536, …] 23, [2384897,
2384896, 1114112, 524288, 262144, 131072, 65536, …] 24, [4227137, 4227136,
2105344, 1048576, 524288, 262144, 131072, 65536, …] 25, [8978569,
8912896, 4194304, 2097152, 1048576, 524288, 262144, 131072, 65536, …] |
||
|
|
Commentaires Appel aux logiciels de théorie des
nombres. Initialisation du compteur (kt) de
record. Boucle d'analyse des nombres de 2 à 100. Prise initiale de valeur de n = nn
et initialisation de la liste des totient en commençant par n lui-même. Boucle d'itération sur les totients
en chaine. Calcul du totient (phi) et mise dans
la liste L. En fin d'itération (n = 1), arrêt de
la recherche (break) Fin de condition (fi) et fin de boucle
(od). La quantité d'itérations trouvée
pour le nombre n est placéé en q. Fin de programme. En bleu, le résulta de traitement
pour n jusqu'à 100. |
|
Voir Programmation – Index
|
|
||
|
Phi de
sigma Nombres
pour lesquels le totient de la somme des diviseurs est égal au nombre. |
1, 2, 8, 12, 128, 240, 720, 6 912,
32 768, 142 560, 712 800, … |
|
|
Somme
des diviseurs Nombres pour
lesquels la somme
des diviseurs est égale à la somme des diviseurs de son totient.
|
n, Sigma(n), Phi(n) et
Sigma(phi(n))
1 , 1 , 1,
1
87
, 120 , 56, 120
362
, 546 , 180, 546 1257
, 1680 , 836,
1680 1798
, 2880 , 840,
2880 5002
, 7812 , 2400,
7812 9374 , 14520 ,
4536, 14520 |
|
|
Liste des nombres:
"sigma" =
"phi-sigma" jusqu'à 1
million [1, 87, 362, 1257, 1798, 5002, 9374,
21982, 22436, 25978, 35306, …] Suite et autres
relations entre sigma et phi >>> |
||
![]()
|
|
||
|
Nombre non-totient Nombre
qui n'est jamais totient d'un nombre. Nombre
pour lequel j (x) = n n'a pas de solution. Nombre
n pour lequel, il n'existe aucun nombre x ayant une quantité n
de nombres premiers entre eux
inférieurs à lui. Propriétés Tous
les nombres impairs sont non-totients (sauf 1). Tous
les nombres premiers moins un sont non-totients. Valeurs des premiers
non-totients pairs 14, 26, 34, 38, 50, 62, 68, 74, 76, 86, 90,
94, 98, 114, 118, 122, 124, 134, 142, 146, 152, 154, 158, 170, 174, 182, 186, 188,
194, 202, 206, 214, 218, 230, 234, 236, 242,
244, 246, 248, 254, 258, 266, 274, 278, 284, 286, 290,
298, 302, 304, 308, 314, 318 … >>> |
||
|
Programme listant tous les nombres
non-totients
Programme pour copie dans Maple restart; with(NumberTheory): A := proc (n) options operator,
arrow; if InverseTotient(n) = {} then n end if end proc; seq(A(i), i = 1 ..
20); nops([%]); |
Programme Maple Pour exécuter le programme, vérifier que le logiciel
est en mode maths et non texte. Sinon, clic droit et convertir en maths 2D. Si vous avez une ancienne version de Maple, utilisez
with(numtheory) et l'instruction invphi. Voir Trucs Maple |
|
|
|
||
|
Un nombre
n est faiblement totient si pour tout nombre m > n on a:
Le nombre 60 est faiblement totient car son
totient est 16, et c'est le plus grand nombre avec ce totient. Les primorielles
et leur produit par un nombre premier impair font partie de cette liste. |
Liste 2, 6, 12, 18, 30, 42, 60, 66, 90,
120, 126, 150, 210, 240, 270, 330, 420, 462, 510, 630, 660, 690, 840, 870,
1050, 1260, 1320, 1470, 1680, 1890, 2310, 2730, 2940, 3150, 3570, 3990, 4620,
4830, 5460, 5610, 5670, 6090, 6930, 7140, 7350, 8190, 9240, 9660, 9870, … |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette
page |
![]()