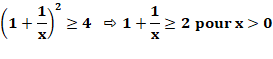|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉRIVÉE – Novices Vous savez ce qu'est une vitesse. Vous savez alors ce qu'est
une dérivée. Dérivée: taux de variation d'une grandeur. Vitesse: taux de variation de la distance
parcourue. Accélération: taux de
variation de la vitesse. Coucou! Je suis en première et je voudrais démarrer d'un bon pas >>> |
|
|
||
|
·
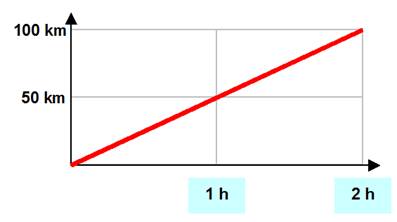
Je suis sur une belle route de campagne et je note la
distance parcourue: · En 1 heure, j'ai
fait 50 km; · La 2e
heure, j'ai fait 50 km; · Total: 100 km. ·
Ma vitesse est vraiment régulière: · Elle est de 50 km /
h. ·
On observe une simple droite sur le graphique. |
Ce
graphique montre la distance parcourue en fonction du temps. |
|
Note: Belle balade
durant laquelle j'aurais pu composer une jolie ballade
(poème épique) >>>
|
·
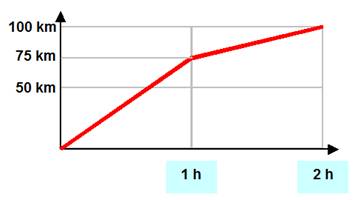
Le lendemain je note: · En 1 heure, j'ai
fait 75 km; · La 2e
heure, j'ai fait 25 km; · Total: 100 km. ·
Le trafic est fluctuant, ma vitesse n'est pas la même
selon l'heure: ·
Elle est de 75 km / h la première heure; · Et de 25 km / h la
deuxième. ·
La vitesse est facile à observer sur le graphe. ·
C'est la pente
de la droite dessinée. |
La
première heure, je vais plus vite que la seconde. La pente de la droite
témoigne de la vitesse. |
|
|
||
|
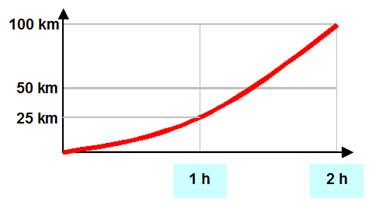
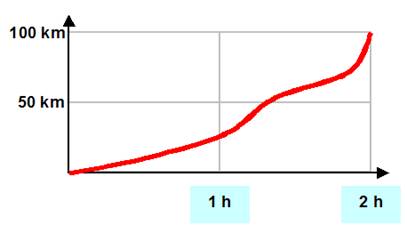
·
Un sportif en voiture se lance départ arrêté et accélère: · En 1 heure, il fait
25 km; · La 2e
heure, il fait 75 km; · Total: 100 km. ·
Quelle est sa vitesse? · Elle change
constamment. ·
C'est là qu'intervient la notion de dérivée. ·
Comment calculer la pente de la tangente en tout point? |
La
vitesse c'est la pente de la courbe. Mais quelle pente? |
|
|
·
La courbe est décrite par la fonction ·
y = a
x2
·
Avec au point extrême Soit 100 = a . 22 Et a = 25 ·
L'équation de la courbe devient: · y = 25 x² avec x = 1 => y = 25 ·
Effectivement, le sportif avait noté qu'il avait fait
25 km au bout de la première heure. ·
On apprendra que: ·
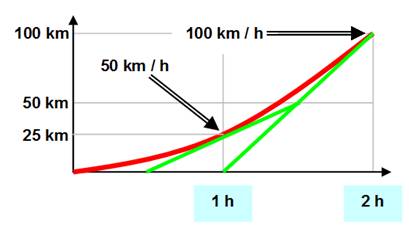
la fonction dérivée de y = a x² est y' = 2 a x ici y' = 50 x ·
La constante 2a = 50 (une accélération) permet de calculer la vitesse instantanée. Elle
vaut 50 km/h au point x = 1 heure et elle vaut 100 km/h au point x = 2
heures. |
On note la distance en fonction du temps: d = f(t). Mais pour être plus général, nous allons prendre: y = f(x) Ici: y = 25 x² La dérivée est y' = 50 x Avec x = 1, y' = 50 km/h; C'est ma vitesse au temps 1 heure (droite tangente en vert). Avec x = 2, y' = 100 km/h; C'est ma vitesse au temps 2 heures (2e droite tangente en
vert). |
Voir Accélération
Vous ne l'avez pas demandé …
|
Je me pose une question Au
bout d'une heure, la vitesse
(instantanée) est déjà de 50 km/h, alors
que je n'ai parcouru que 25 km. Je trouve
cela bizarre. Voyons
cela en prenant une échelle de temps plus petite. Voyons
ce qui se passe toutes les cinq minutes. Explication Sur
ce tableau à gauche, les valeurs trouvées pour une heure
et deux heures de route. Notamment 25 km parcourus avec une vitesse au bout
d'une heure qui est grimpée à 50 km/h (sujet de notre interrogation).
Sur
le tableau à droite, le même type de calcul mais avec les minutes comme unité de temps. Nos valeurs au
bout d'une heure (60 min.) se retrouvent. Nous constatons que la vitesse
croit progressivement pour atteindre 50km/h. Calculons
la distance parcourue toutes les tranches de cinq minutes. Un calcul approximatif serait
le suivant: autour du temps 5 min, je prends la vitesse moyenne (0 + 4,17) /
2 = 2,08 que je multiplie par la tranche de temps de 5 min. soit 5/60 heure.
Résultat: 0,17. La somme de ces parcours élémentaires atteint les 25 km. Nous
voilà rassurés. |
|
|
||
|
·
Si je veux calculer la vitesse à laquelle je roule à 1
heure pile (pour pouvoir l'afficher sur mon compteur, par exemple) ·
Je regarde la distance parcourue au compteur : 25 km. ·
Je roule un peu, disons 10 minutes et je note à nouveau
la distance parcourue: je trouve 35 km. ·
Le calcul classique de vitesse donne · 10 km en 10
minutes; 6
fois plus en 1 heure, soit
60 km / heure. |
|
|
|
·
Non, mais attendez, j'ai pu accélérer ou ralentir en 5
minutes !!! C'est vrai, alors, il faut mesurer pendant un tout petit intervalle
de temps pour éviter trop d'erreurs dues aux fluctuations de vitesse. · Plus le temps de mesure
est court, plus la vitesse instantanée est précise. Mais, il faut un
compteur kilométrique très précis. Combien de mètres en 10 secondes et
même moins ? ·
Newton a trouvé un truc
pour s'en sortir dans tous les cas ... si on connaît la fonction (comme
ci-dessus avec y = ax²). Les mathématiciens modernes ont justifié la méthode
des dérivées, encore utilisée aujourd'hui. |
||
Merci à Valérie G. pour les conseils
d'amélioration
|
F
et F' sont sur un bateau. F tombe à l'eau. Que fait F'. Il dérive. |
Voir Pensées & humour
|
Problème Comment montre que la fonction f(x) = x + 1/x est
toujours supérieure ou égale à 2 pour tout nombre positif non nul ? Passage par un extremum Ayant appris la notion de dérivée, il est
possible de répondre à la question. Le minimum (ou le maximum) de cette
fonction sera atteint pour une dérivée nulle. Or, nous le verrons plus tard, la dérivée de
cette fonction est f'(x) = 1 – 1/x²
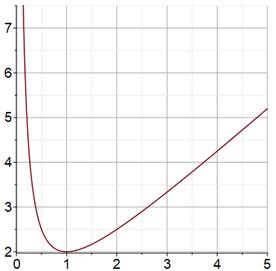
qui est nulle pour x = 1 et alors f(x) = 2. Pour x = 2, on a f(x) = 2 + 1/2 =
2,5 qui est plus grande et pour x = 1/2, f(x) = 1/2 + 2 = 2, 5 qui est aussi
plus grand. La fonction passe par un minimum pour x = 1 et f(x) est toujours
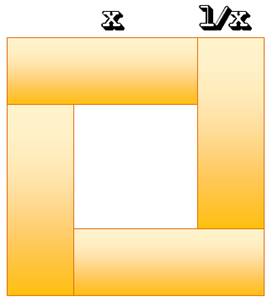
supérieure ou égale à 2. Le graphe de la fonction le montre. Solution imagée Sans recours aux dérivée, il astucieusement
possible de trouver le même résultat. L'idée consiste à utiliser la figure du carré à
droite. Son aire vaut: A = (x + 1/x)² L'aire des quatre rectangles vaut toujours 4 x 1
= 4. Et l'aire du carré lui est toujours supérieure (Aire du petit carré en
plus). Conclusion:
|
|
![]()
|
Suite |
·
Un exercice
d'approche des dérivées ·
Approche des dérivées via le
carré ou le cube des nombres ·
Dérivées ·
Intégrale – Approche
avec 1/x |
|
Voir |
· Dérivées – Glossaire · Équations différentielles
– Glossaire · Vitesse – Glossaire |
|
Cette
page |
![]()