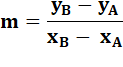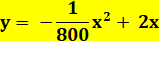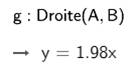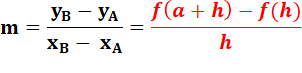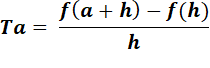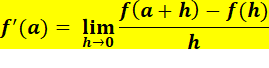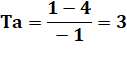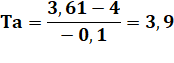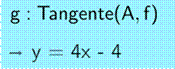|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉRIVÉES Approche en classe de première Exemples d'activités et
exercices, expliqués pas à pas. Notions de: pente, coefficient directeur, dérivée et tangente. |
|
|
||
|
Le
coefficient directeur représente la pente de la droite avec un signe:
La figure
illustre quelques cas de calcul du coefficient directeur m des droites:
|
|
|
|
|
||||||
|
Problème Un canon
tire un boulet qui suit une trajectoire parabolique. Ce boulet s'élève et
retombe 1600 m plus loin. On
modélise la trajectoire par: Quel est l'angle
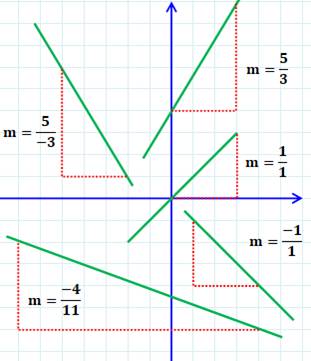
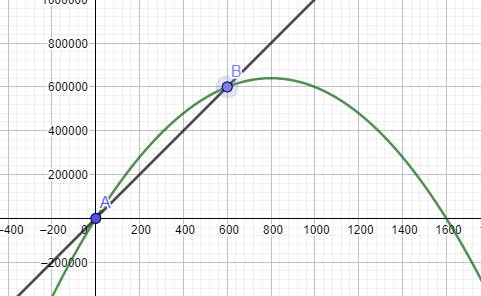
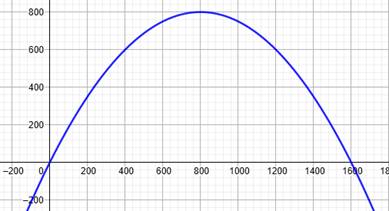
du canon avec l'horizontale ? Allure du graphe La courbe
représentant cette fonction est une parabole dont le sommet est atteint pour
x = 800. La valeur
atteinte (y = 640 000 environ) est 800 fois supérieure la valeur de x (=
800). |
On observe une
démesure entre les
échelles des axes. |
|||||
|
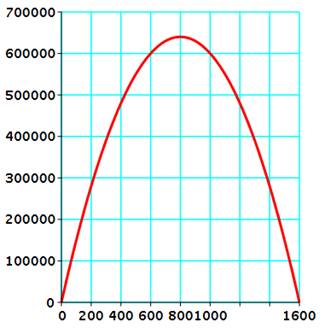
Activité avec GéoGebra Cet outil est accessible
sur Internet gratuitement. C'est un des outils utilisés au lycée. Son utilisation est très simple après un peu de pratique |
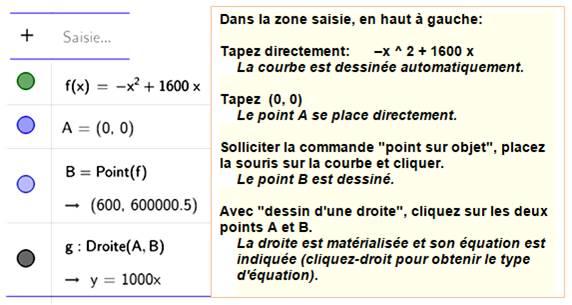
Procédure pour tracer la courbe, les points et la
droite
|
|||||
|
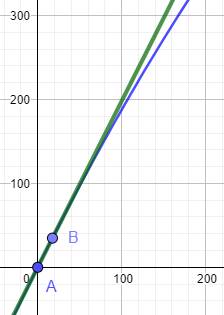
Graphe Parabole en vert et droite AB en noir. La rotation de la molette de la souris permet l'ajustement de
l'échelle
Cette flèche cliquée permet de faire glisser la figure en l'agrippant
avec la souris (clic-gauche maintenu). |
|
|||||
|
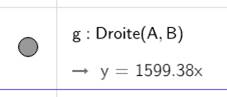
Coefficient directeur Le point B est déplacé le plus près possible du point A (en ajustant
l'échelle avec la molette). La fenêtre à gauche montre l'évolution
du coefficient directeur de la droite AB, lequel tend vers 1600. |
|
|
||||
|
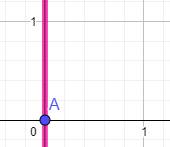
Angle de la tangente La pente de la tangente est égale
au coefficient directeur
arctan(1600) = 1,57 radian = 89,96° Un angle proche de 90°. |
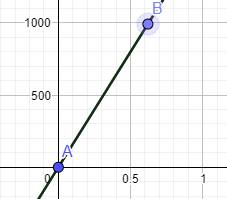
Graphe avec même échelle en x et y
Avec cette
échelle, la tangente est pratiquement verticale |
|||||
Voir Exemples
d'utilisation de GeoGebra
|
|
||
|
Problème Sur une
plaine plate, un canon tire un boulet qui suit une trajectoire parabolique.
Ce boulet s'élève à 800m et retombe 1600 m plus loin. Modéliser
la trajectoire et calculer l'angle du canon avec l'horizontale. Allure du graphe La courbe
représentant cette fonction est une parabole dont le sommet est atteint pour
x = 800 et y = 800 Le sol étant plat, la parabole est symétrique et
son maximum est atteint pour x = 1600
/ 2 = 800. |
Graphe avec même
échelle en x et en y. |
|
|
Modélisation de la trajectoire Équation générale de la parabole et calcul des
coefficients en sachant que la courbe passe par trois ponts. |
y = ax² + bx + c 0 = 0 + 0 + c => c = 0 0 = 1600²a + 1600b => 1600a = –
b 800 = 800²a + 800b => 1 = 800a +
b 1 = 800a – 1600a => a = – 1 / 800 b = – 1600 a = 2
|
|
|
Pente avec GeoGebra Même procédure que ci-dessus pour les points A et
B et la droite AB. Alors la fenêtre nous indique:
Un coefficient
directeur qui tend vers m = 2. Angle de la pente de la tangente à
l'origine arctan(2) = 1,107 radian = 63,43 ° |
|
|
|
|
||
|
On
rappelle la valeur du coefficient directeur de la droite AB; Il est
exprimé également en appelant h l'écart entre les deux abscisses. |
|
|
|
Soit f une fonction définie sur un intervalle I,
et a et a +
h (h différent de 0) deux éléments de l'intervalle I: |
||
|
Le quotient présenté ci-dessus est appelé taux d'accroissement de la fonction f entre a et
a + h. |
|
|
|
Si le taux d'accroissement tend vers un nombre réel quand h tend vers
0, on dit que la fonction f est dérivable
en a. Ce nombre réel est la dérivée
de la fonction f en a. On note f'(a) qui se lit f prime de a. |
|
|
|
Exemple avec la fonction f(x) = x² Point A (2 ; 4) Avec B (1 ; 1) : h = -1
Avec B (1,9 ; 3,61): h = -0,1
Passage à la limite
La dérivée de x² au point d'abscisse 2 est égale
à 4. |
|
|
|
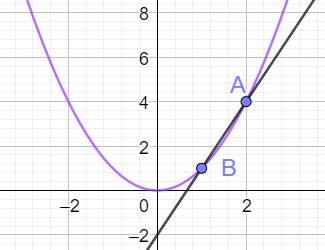
Tangente La tangente à
la courbe représentative de f au point d'abscisse a est la droite passant par
le point de la courbe de coordonnées (a; f(a)) et ayant pour coefficient
directeur f'(a). Le coefficient directeur de la tangente en A est
égal à la dérivée de x² en A, soit 4. Avec y = 4x + b, on détermine b en notant que la
droite passe par le point A: Équation de la tangente: y = 4x – 4, conformément
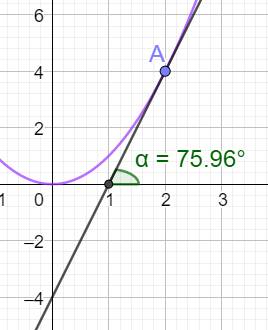
avec ce que nous indique le logiciel GeoGebra. Angle de la pente de la tangente à
l'origine arctan(4) = 1,326 radian = 75,96 ° |
|
|
![]()
|
Retour |
|
|
Suite |
·
Dérivées ·
Intégrale
– Approche avec 1/x |
|
Voir |
· Dérivées – Glossaire ·
Équations
différentielles – Glossaire · Vitesse – Glossaire |
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Analyse/DerivInt/Approche.htm
|
![]()