|
|||||||||||||||||||||||||||||
![]()
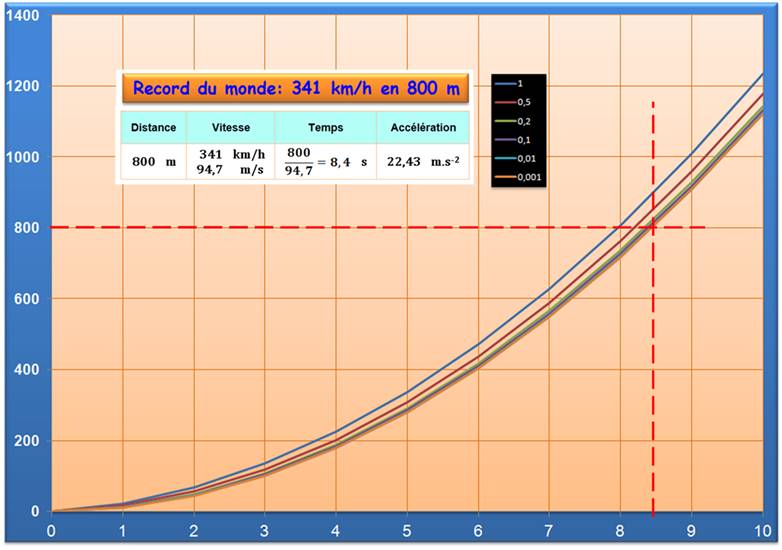
Performance des voitures de course
|
|
avec
une Ford GT en 17 mai 2012. Une
accélération départ arrêté exceptionnelle! |
|
|
|
|
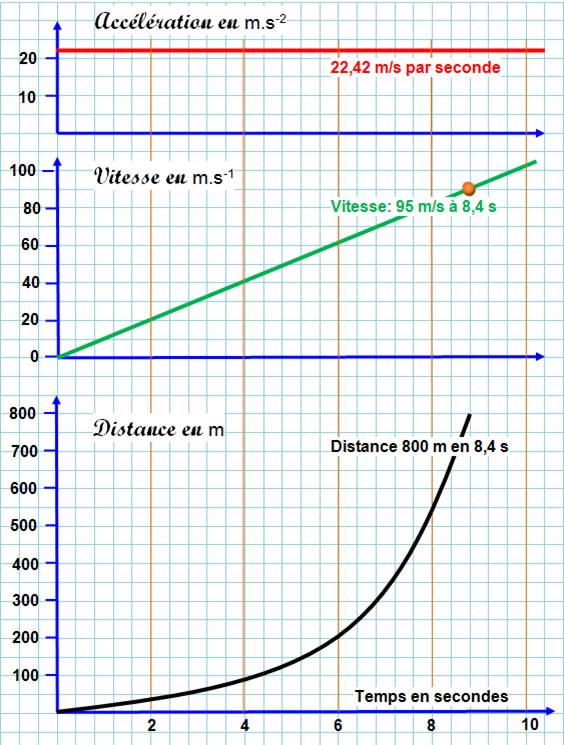
Lorsque le mouvement
d'un objet est modifié, soit par un changement de vitesse
ou par un changement de direction, on dit
qu'il a reçu une accélération. Une
accélération n'est donc pas nécessairement une augmentation de vitesse. |
|
|
|
|
|
|
|
|
|
||
|
|
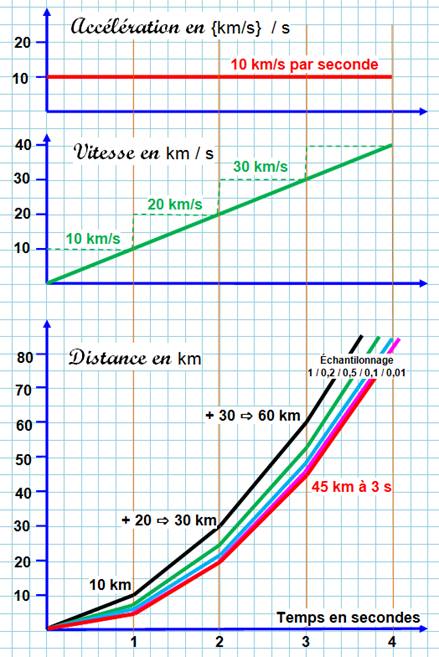
Plus le calcul est fin et plus la courbe se stabilise. elle atteint
une limite. En l'occurrence pour 3 secondes la distance s'établit à 45 km. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
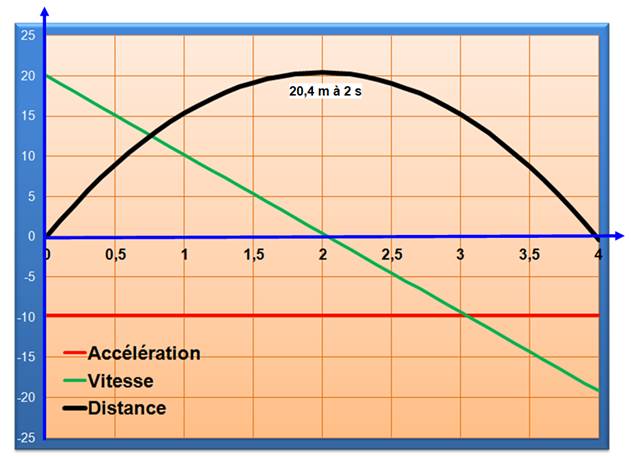
L = 20 x 2 – ½ x 9,8 x 22
= 20,4 m |
|
Voir Calcul
complet
|
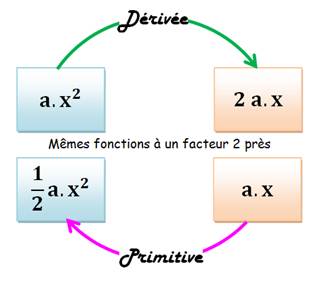
Nous
avons appris à nous méfier de l'accélération. Le mode de calcul fait
intervenir la notion de primitive d'une
fonction. La primitive
ou antiderivative comme disent les Anglais
est l'inverse de la dérivée.
Retenons
que le calcul de la valeur de l'accélération passe par la formule indiquée
ci-dessus. |
Voir Calcul intégral / Exemple de calcul / Infinitésimaux
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Physique/AccelPhy.htm |