|
|||||||||||||||||||||||||||||
![]()
|
SOMME DE NOMBRES Parmi Q nombres pris au
hasard, il existe q nombres dont la somme est divisible par q. Quelle est la
valeur de Q en fonction de q? |
|
|
|
|
Avec deux nombres (Q = 2)
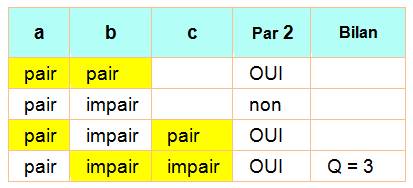
Avec trois nombres (Q = 3)
D'une manière générale (Q = n)
Bilan Quelle que soit la quantité de nombres choisis au
hasard, il est impossible d'assurer que leur somme sera paire.
|
|
|
Cas
q = 2 |
|
|
Bilan q
= 2 Avec trois nombres choisis au hasard, il existe
au moins une paire de nombres dont la somme est divisible par 2. |
|
Voir Principe des
tiroirs
|
|
|
|
0 0 1 1 2 2
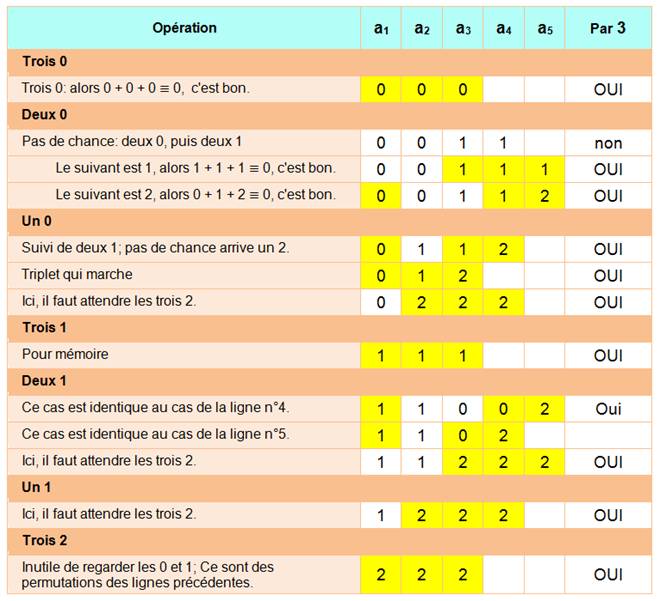
Analyse expérimentale
Analyse raisonnée
Bilan q
= 3 Avec cinq nombres choisis au hasard, il existe au
moins un triplet de nombres dont la somme est divisible par 3. |
|
|
|
|
|
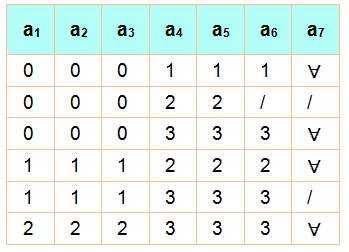
Bilan q
= 4 Avec sept nombres choisis au hasard, il existe au
moins un quadruplet de nombres dont la somme est divisible par 4. Exemple Sept nombres: 7, 9, 11, 15, 17, 21, 54 Valeurs mod 4: 3 , 1,
3,
3, 1, 1,
2 Nombres retenus: 11 + 15 + 17 + 21 = 64 = 16 x
4 |
|
|
Cas
q = 5 |
|
|
Bilan q
= 5 Avec neuf nombres choisis au hasard, il existe au
moins un quintuplet de nombres dont la somme est divisible par 5. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/aaaDIVIS/Somme.htm
|
![]()