|
|||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ – Débutants Critères
de divisibilité par 2, 3, 4, 5 … Comment appliquer? |
|
|
||
|
|
Ces 15
personnages sont en rang par 3, exactement. On dit que 15 est partageable ou
divisible par 3.
Ces 16
personnages sont en rang par 3, mais un individu reste à part. On dit que 16
n'est pas divisible par 3. |
|
|
|
||
|
|
Chaque
fois qu'il y 2, 4, 6, 8, 10, 12, 14 … enfants, il est possible de les mettre
en rang par 2, exactement. Mais
s'il y a 1, 3, 5, 7, 9, 11, 13 … enfants, ce n'est pas possible d'y arriver
exactement; Il en reste 1 sans camarade. |
|
|
Règle Un nombre est divisible par 2, s'il se termine par 0, 2, 4, 6 ou 8
(s'il est pair). |
||
|
|
||
|
|
Chaque
fois qu'un nombre n'a pas d'unité, c’est-à-dire qu'il se termine par 0, alors
il est divisible par 10. C'est
le cas de divisibilité le plus facile à retenir. |
|
|
Règles Un nombre est divisible par 10, s'il se termine par 0. Un nombre est divisible par 100, s'il se termine par 00. |
||
|
|
||
|
|
Je
compte de 5 en 5: 0, 5,
10, 15, 20, 25 … |
|
|
Règles Un nombre est divisible par 5, s'il se termine par 0 ou 5. Un nombre est divisible par 50, s'il se termine par 00 ou 50. Un nombre est divisible par 25, s'il se termine par 00, 25, 50 ou 75. |
||
|
|
||
|
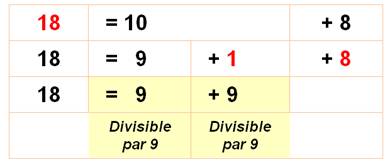
10 = 9 + 1.
100 =
99 +
1 = 9 x 11 + 1 1000 = 999 + 1 = 9 x 111 + 1 |
Le
nombre 18 peux l'écrire 18 = 10 + 8.
Beauté
de la chose: 1 + 8 est la somme des chiffres
de 18. Et, c'est toujours comme cela! |
|
|
Règles Un nombre est divisible par 9, si la somme de ses chiffres est
divisible par 9. |
||
|
En pratique Addition de tous les chiffres du nombre, et Remplacement des 9 par 0 au fur et à mesure des calculs. |
||
|
Exemples 1 107 1 111 104 8 888 888 889 En pratique
(toutes ces opérations peuvent se faire mentalement):
|
||
|
|
||
|
|
123 Plus
simple on élimine les 3 et ses multiples au fur et mesure qu'ils se présentent. 123 456 123 456 789 3 + 9 + 7 + 8 7 + 8 15 |
|
|
Règles Un nombre est divisible par 3, si la somme de ses chiffres est
divisible par 3. Un nombre est divisible par 6, s'il est divisible par 3 et par 2. |
||
Bilan
|
Nous
venons de voir deux méthodes de recherche de la divisibilité.
Ces
méthodes peuvent être combinées comme pour 6. |
![]()
|
Débutants |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
Accès aux nombres: |
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiDb.htm |
![]()