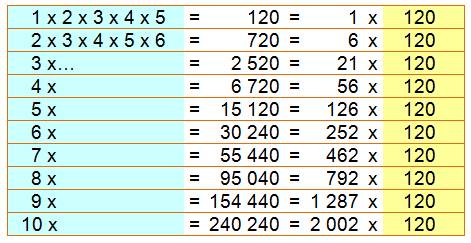|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
CRITÈRES de DIVISIBILITÉ Comment déterminer
rapidement si un nombre est divisible par un autre
? Quelles sont les formes des nombres divisibles par un autre ? Ici, nous
passons en revue les meilleurs critères pour les divisibilités par 2, 3, 4,
5, 6, … jusqu'à 1111. Deux méthodes systématiques
sont expliquées en clé de divisibilité. La
solution générale pour une divisibilité par un nombre premier est explicitée en: méthode par unité tronquée. |
|
Notations |
|
|
R.N. =
Somme numérique. =
somme des chiffres jusqu’à n’obtenir qu’un seul chiffre. =
preuve par neuf. Exemple R.N.
(3456) = 3 + 4 + 5 + 6 = 7 + 5 + 6 = 12 + 6 = 3 + 6 = 9 (= 0) du du
= nombre formé des dizaines et unités. u = chiffre des unités, d = chiffre des dizaines, c = centaines, m = milliers. (…)
= tous les autres chiffres du nombre En
jaune classique et
relativement simple; |
|
|
Par |
Règle |
Exemple |
Commentaires |
Liens |
|
|
2 |
|
124 |
4 est pair |
||
|
3 |
|
123 |
R.N.(123) = 1 + 2 + 3 = 6 |
||
|
4 |
ou encore: 2d + u est
divisible par 4. |
565 544 |
44 = 11 x 4 |
||
|
5 |
u
={0, 5}. |
565 545 |
|||
|
6 |
|
288 |
R.N.(288) = 9 |
||
|
71 |
On
soustrait 2 fois le dernier. On
vérifie si le résultat est divisible par 7. |
364 |
36 – 2x4 = 28 28 = 7x4 |
||
|
72 |
|
364 |
3x3+ 6 =15 5x3 + 6 = 21 |
|
|
|
73 |
|
8 638 |
638 – 8 = 630 = 90 x 7 |
|
|
|
8 |
|
565 448 |
120/8 = 15 44 + 8/2 = 48 |
||
|
9 |
|
182 736 |
R.N. = 0 |
||
|
10 |
|
100 |
|||
Carte bancaire
|
Son
n° et son code d'authenticité associés dans une addition particulière
(algorithme de Luhn) conduisent à un nombre divisible
par 10, preuve de sa validité. >>> |
|
111 |
|
33 33 33 3 33 33 |
oui non |
|
|
112 |
|
484 913 |
4 + 4 - 8 = 0 9 + 3 - 1 = 11 |
|
|
113 |
|
181 907 |
Sp = 8+9+7=24 Si = 1+1+0=2 Sp-Si= 22 |
|
|
114 |
|
1 353 |
135-3 = 132 13-2 = 11 |
|
|
115 |
|
1 353 |
13 + 53 = 66 |
|
|
12 |
4
(…) + du. |
144 |
4x(1) + 44 = 48 = 12 x 4 |
|
|
131 |
|
16 042 |
042 – 16 = 26 26 = 13 x 2 |
|
|
132 |
|
16 042 |
1604 + 4x2 = 1612 161 + 4x2 = 169 16+ 4x9 = 52 |
|
|
7, 11 et 13 |
|
12 357 345 |
357 – (12 + 345) = 0 |
|
|
15 |
|
45 |
|
|
|
16 |
|
180 016 |
||
|
17 |
|
58 752 |
5875 – 5x2 = 5865 586 – 5x5 = 561 56 – 5x1 = 51 |
|
|
19 |
Voir Nombre
19 |
14 991 |
1499 + 2x1 = 1501 150 + 2x1 = 152 15 + 2x2 = 19 |
Note: les
méthodes par itération ou par épluchage sont
aussi désignées comme critère dominos.
|
20 |
|
80 |
Unité = 0 et dizaine => 8 / 2 = 4 |
|
|
231 |
|
276 |
27 + 7 x 6 = 69 |
|
|
232 |
|
2 829 |
28 + 3x29 = 115 |
|
|
24 |
16
(…) + cdu. |
29 640 |
16 (2+9) + 640 = 176 + 640 = 816 816 = 24 x 34 |
|
|
25 |
|
275 |
|
|
|
27 |
|
33 345 |
33 + 345 = 378 378 = 27 x 14 |
|
|
29 |
|
3 567 |
356
+ 3x7 = 377 37
+ 3x7 = 58 |
|
|
31 |
|
3 813 |
381
– 3x3 = 372 37
– 3x2 = 31 |
|
|
33 |
|
99 |
|
|
|
36 |
|
432 |
|
|
|
371 |
|
45 695 |
45 + 695 = 740 740 = 20 x 37 |
|
|
372 |
|
45 695 |
4569 – 11x5 = 4514 451 – 11x4 = 407 40 – 11x7 = –37 |
|
|
40 |
et
u = 0. |
49 360 |
3x2 + 6 = 12 => 12 = 4x3; et u = 0 |
|
|
41 |
|
50617 28349 |
50617 + 28 349 = 78 966 Suite en dessous |
|
|
41 bis |
|
78 966 |
7896 – 4x6 = 7872 787 – 4x2 = 779 77 – 4x9 = 41 |
|
|
431 |
|
19 608 |
1960 – 30x8 = 1720 172 – 30x0 = 172 17 – 30x2 = – 43 |
|
|
432 |
|
19 608 |
196 – 3x8 = 172 |
|
|
45 |
|
5535 |
10 x (5+5+3) + 5 = 135 = 3 x 45 |
|
|
471 |
|
564 |
56 – 14x4 = 0 |
|
|
472 |
|
580 215 |
5802 + 8x15 = 5922 59 + 8x22 = 235 |
|
|
48 |
|
59 232 |
16 x 5 + 9232 = 9312 = 48 x 194 |
|
|
50 |
|
|
|
|
|
531 |
|
636 |
63 + 16x6 = 159 |
|
|
532 |
|
65 402 |
654 – 9x2 = 636 6 – 9x36 = –318 |
|
|
61 |
|
732 |
73 – 6x2 = 61 |
|
|
671 |
|
804 |
80 – 20x4 = 0 |
|
|
672 |
|
82 678 |
826 – 2x78 = 670 |
|
|
71 |
|
|
|
|
|
73 |
|
|
|
|
|
77 |
|
17 094 |
94 – 17 = 77 |
|
|
79 |
|
|
|
|
|
83 |
|
|
|
|
|
891 |
|
1 068 |
106 +9x8 = 178 |
|
|
892 |
|
109 826 |
1098 – 8x26 = 890 |
|
|
91 |
|
1 092 |
109 – 2x9 = 91 |
|
|
96 |
|
|
|
|
|
97 |
|
2 425 |
242 – 29x5 = 97 |
|
|
991 |
|
86922 |
8+6+2+2= 18 8+9+2-6-2= 11 |
|
|
992 |
|
1 188 |
11 + 88 = 99 |
|
|
100 |
d
= 0 et u = 0. |
|
|
|
|
101 |
|
12 423 |
1 – 24 + 23 = 0 |
|
|
1111 |
|
13 653 |
13 + 653 = 666 |
|
|
1112 |
|
|
||
|
125 |
|
7 375 |
375 |
|
|
137 |
|
|||
|
143 |
|
14 157 |
157 – 14 = 143 |
|
|
200 |
|
11 800 |
800 |
|
|
250 |
|
|
|
|
|
303 |
|
373 902 |
37 + 3902 = 3939 |
|
|
333 |
|
|
|
|
|
399 |
|
2 394 |
23 + 4 x 94 = 399 |
|
|
500 |
|
1 500 |
|
|
|
909 |
|
373 902 |
37 + 3902 = 3939 |
|
|
999 |
|
111 807 |
11 + 1807 = 1818 |
|
|
1000 |
c
= 0, d = 0 et u = 0. |
123 000 |
|
|
|
1001 |
|
1 235 234 |
1 – 235 + 234 = 0 |
|
|
1111 |
|
135 8753 |
135 + 8753 = 8888 |
Voir aussi Divisibilité par l'unité tronquée / Empreinte de divisibilité /
Divisibilité "du"
/ Divisibilité "cdu"
Aussi: 133 / 222 / 240
/ 504 / 512 / 576 / 641 / …
|
|
|
|
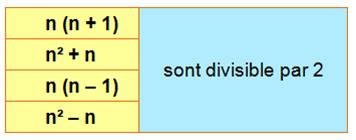
Deux
nombres consécutifs
Parmi deux nombres consécutifs, il y en a toujours un
qui est pair. Le produit de
deux nombres consécutifs est toujours pair.
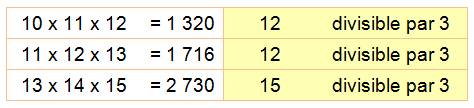
Trois
nombres consécutifs
Parmi trois nombres
consécutifs, il y en a toujours un qui est divisible par 3. Le produit de
trois nombres consécutifs est toujours divisible
par 6. Remarquons que 6 =
2 x 3 = 3 ! (factorielle 3)
Le produit de r nombres consécutifs est toujours divisible par r!. Voir Démonstration
Exemples avec r = 5
|
|
Voir Coefficient
du binôme / Factorielle tronquées et somme
des facteurs / Identités remarquables et
consécutifs
|
|
|
|
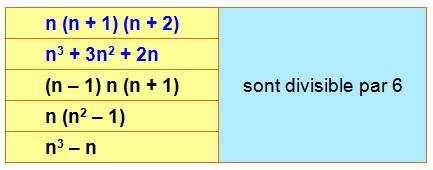
Deux
nombres pairs consécutifs Parmi deux nombres
consécutifs pairs consécutifs, l'un des deux est divisible par 4. Le produit de
deux nombres PAIRS consécutifs est toujours divisible
par 8.
Trois nombres consécutifs, le central est impair Parmi trois nombres
consécutifs, l'un est divisible par 3. Comme le central est impair, il est
flanqué de deux nombres pairs consécutifs, dont le produit est divisible par
8. Le produit de
trois nombres consécutifs dont le central est impair, Voir Divisibilité par 24 |
|
|
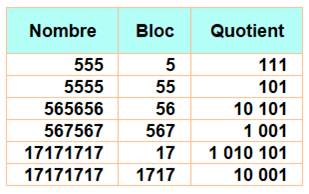
Propriété Un
nombre formé de blocs répétitifs est divisible par ce bloc. Exemples
Explication: 555 = 500 + 50 + 5 = 5 (100 + 10 + 1) = 5
x 111 565656
= 560000 + 5600 + 56 = 56(10000 + 100 + 1) = 56 x 10101 |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiGe.htm |
![]()