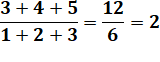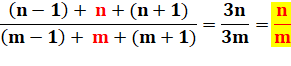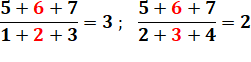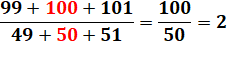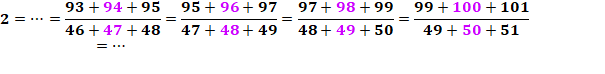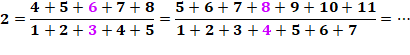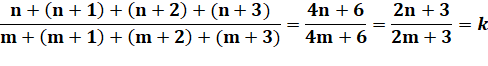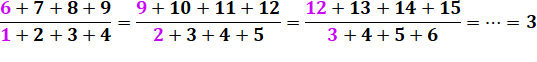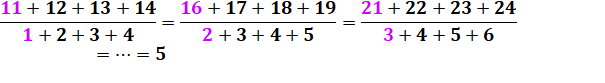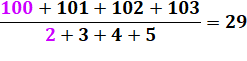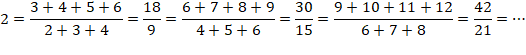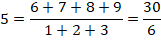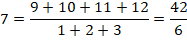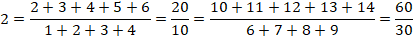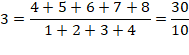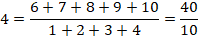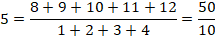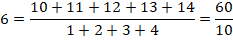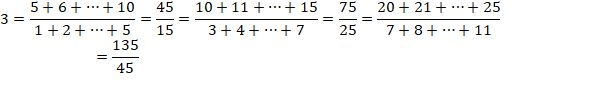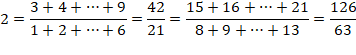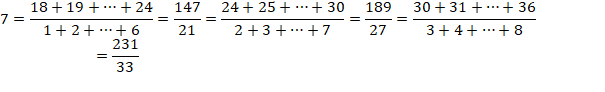|
|||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ & CURIOSITÉS Divisibilité d'une somme de
nombres consécutifs par une somme de nombres consécutifs. |
Voir Nombre
entier / quotient /
consécutifs
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Accès aux nombres |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/DivisiSS.htm
|
![]()