|
|||||||||||||||||||||||||||||
![]()
|
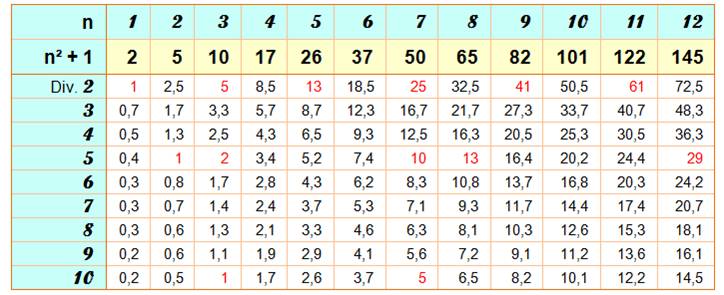
Divisibilité de n² + 1 On connait les cas de divisibilité de n² – 1. Que peut-on dire de n² + 1? Ce nombre est parfois divisible
par 2 ou 5, mais jamais divisible par 3, 4, 6, 7, 8, 9 … |
|
|
|
|
Exemples de lecture: n = 3
alors n² + 1 = 9 + 1 = 10 qui est divisible par 2 (2 x 5 = 10), mais pas par 3 (3 x 3, 333… = 10). |
|
Notre bagage
|
Pour allons
prendre la forme générique de n selon la division que nous voulons tester. Si nous cherchons la divisibilité
par 3, nous écrirons n = 3k + h, avec h le reste de la division de n par 3,
soit un des nombres: h = {0, 1, 2}. Pour chacun des
restes possibles, nous étudierons la divisibilité de n² + 1 par 3. Ceci en mettant en évidente des
termes qui sont des multiples de 3 et une constante qui ne l'est pas. Ce qui
montrerait que n² + 1 n'est pas
divisible par 3. |
|
|
|||
|
Un nombre selon sa divisibilité par 3 |
n |
= 3k + h |
|
|
Carré plus 1 |
n² + 1 |
= 9k² +
6kh + h² + 1 |
|
|
Si divisible: h = 0 |
n² + 1 |
= 9k² + 1 non divisible par 3 |
|
|
Si reste h = 1 |
n² + 1 |
= 9k² + 6k + 1 + 1
non divisible par 3 |
|
|
Si reste h = 2 |
n² + 1 |
= 9k² + 12k + 4 + 1
non divisible par 3 |
|
|
n² + 1
n'est pas divisible par 3 |
|||
|
|
|||
|
Un nombre et sa divisibilité par 4 |
n |
= 4k + h |
|
|
Carré plus 1 |
n² + 1 |
= 16k² +
8kh + h² + 1 |
|
|
Si divisible: h = 0 |
n² + 1 |
= 16k² + 1 non divisible par 4 |
|
|
Si reste h = 1 |
n² + 1 Premier facteur Second facteur |
= 16k² + 8k + 1 + 1 = 2 (8k² + 4k + 1)
divisible par 2 non-divisible par 2 non divisible par 4 |
|
|
Si reste h = 2 |
n² + 1 |
= 16k² + 16k + 4 + 1
non divisible par 4 |
|
|
Si reste h = 3 |
n² + 1 |
= 16k² + 24k + 9 + 1
non divisible par 4 |
|
|
n² + 1
n'est pas divisible par 4 |
|||
|
|
|||
|
Un nombre et sa divisibilité par 4 |
n |
= 6k + h |
|
|
Carré plus 1 |
n² + 1 |
= 36k² +
12kh + h² + 1 |
|
|
Si divisible: h = 0 |
n² + 1 |
= 36k² + 1 non divisible par 6 |
|
|
Si reste h = 1 |
n² + 1 |
= 36k² + 12k + 1 + 1 non divisible par 6 |
|
|
Si reste h = 2 |
n² + 1 |
= 36k² + 24k + 4 + 1
non divisible par 6 |
|
|
Si reste h = 3 |
n² + 1 |
= 16k² + 36k + 9 + 1
non divisible par 6 |
|
|
Si reste h = 4 |
n² + 1 |
= 16k² + 48k + 16 + 1
non divisible par 4 |
|
|
Si reste h = 5 |
n² + 1 |
= 16k² + 60k + 25 + 1
non divisible par 4 |
|
|
n² + 1
n'est pas divisible par 6 |
|||
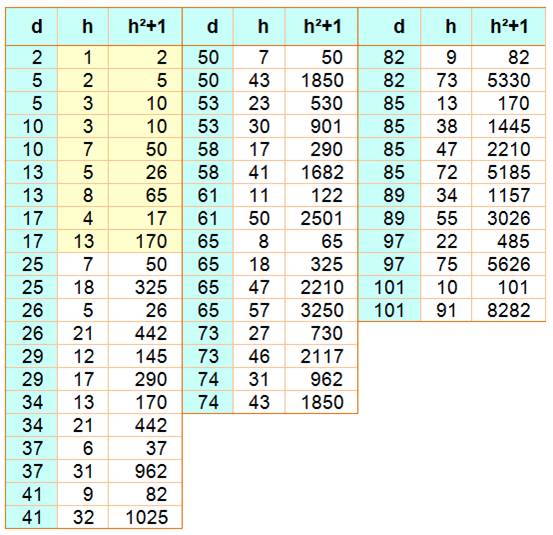
Conclusion à ce niveau
|
Lorsque nous
examinons la divisibilité nous avons en face de nous une expression faite:
L'examen se
simplifie. Le tableau suivant
donne le bilan de cet examen. |
|
|
|
|
n² + 1 n'est jamais divisible par d = {3, 4, 6, 7, 8, 9, 11, 12, 14,
15, 18, 19}
|
|
|
|
|
|
|
|
|
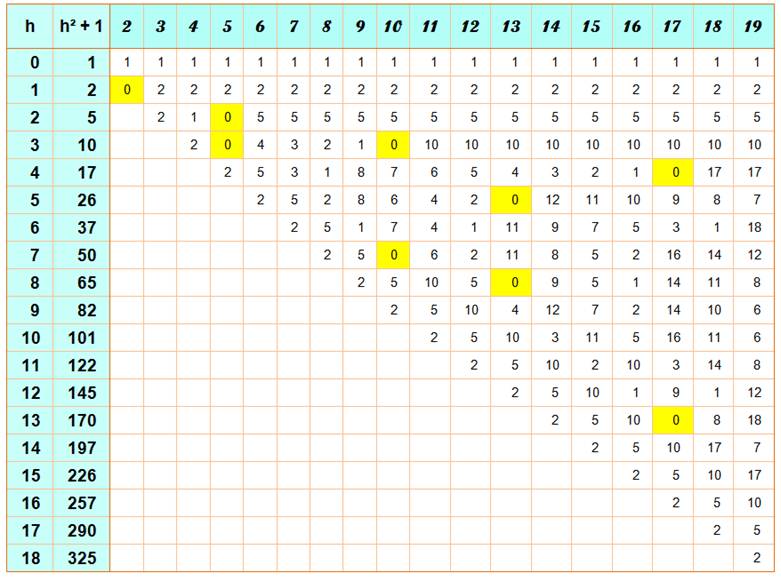
Curieusement, il
existe une majorité de nombres qui ne divise jamais n² + 1 dont les premiers sont:
3, 4, 6, 7, 8, 9, 11, 12, 14, 15, 16, 18, 19, 20, 21, 22, 23, 24, 27 … |
|
|
|
|
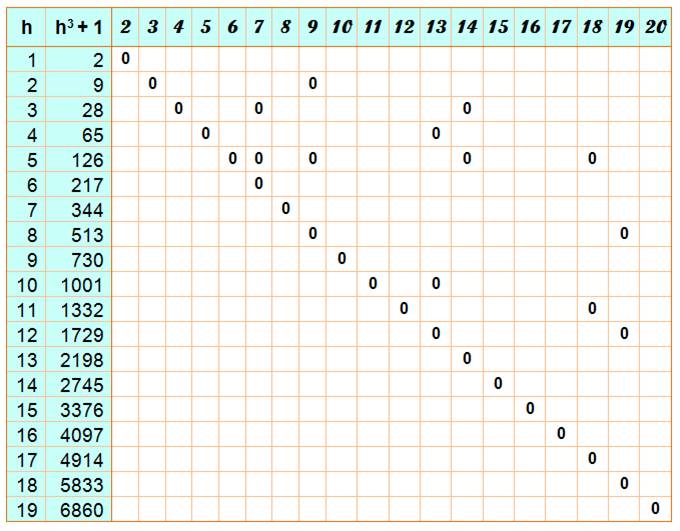
Le tableau présente une
belle diagonale! Pas étonnant, selon l'identité: n3 + 1 = (n
+ 1) (h2 – h + 1), dont divisible par n + 1.
Pour ceux qui voudraient
explorer les puissances supérieures:
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/aaaDIVIS/carrplun.htm
|
![]()