|
Édition du: 03/04/2022 |
|
INDEX |
LOGIQUE |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
LOGIQUE – Spécial Débutants Comment
commencer en logique? Comprendre les bases. |
||
|
|
Sommaire de cette page >>> La
sécurité, c'est logique >>>
L'ascenseur, c'est logique (ET) >>> Coucou
(OU) >>> Mais
NON >>>
La logique de tous les jours >>> Les
deux, mon général ! >>>
La logique et le raisonnement |
Débutants Glossaire |
|
|
||
|
|
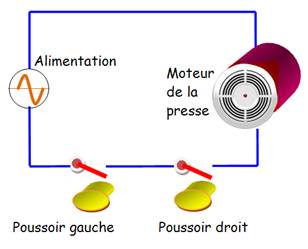
Une presse
Les poignées jaunes de cette presse doivent être actionnées toutes les
deux à la fois pour que la presse fonctionne; La droite ET la
gauche La poignée rouge en avant et un arrêt d'urgence de l'ensemble de
l'installation. Circuit de sécurité
Le moteur ne marche que si les deux poussoirs sont enfoncés en même
temps. |
|
Nous
retenons
|
L'un
ET l'autre (c'est-à-dire: Les deux à la fois) |
Les deux interrupteurs doivent être fermés pour que le courant passe. |
|
|
|||||||||||||||||
|
|
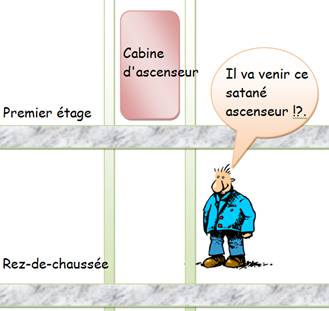
Ascenseur à l'étage
L'ascenseur doit descendre pour me rejoindre Commande logique
Le demi-cercle est le symbole de la fonction ET Table de vérité:
liste de tous les cas possibles.
Il est commode de remplacer le OUI par 1 et le Non par 0 |
||||||||||||||||
* On suppose que cette maison ne
compte que deux niveaux: le RdeC et le 1er .
Suite Logique des ascenseurs
(juniors)
|
|
||||||||||||||||||||||||||||||||||||||
|
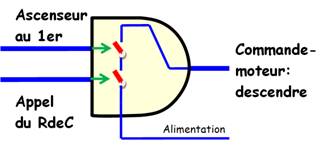
Ajouter le signal témoignant que l'ascenseur est
au 2e.
Si
l'ascenseur est au 1er (A1) ou s'il est au 2e (A2) et
s'il y a un appel du RdeC, alors lancer la commande du moteur.
|
Table de vérité
Commande logique
Commande =
(A1 OU A2) ET
(Appel) |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||
|
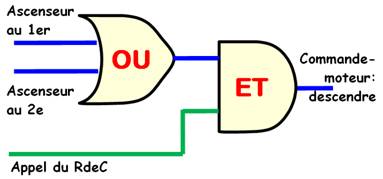
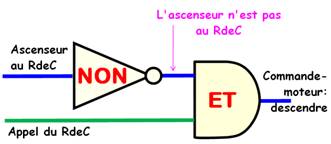
Comment traduire
cela?
Le
connecteur NON inverse les choses: sa
sortie est à 1 si son entrée est à 0 et inversement. Si
l'ascenseur est aux étages, le signal "ascenseur au RdeC" (RdeC)
est à 0; derrière la porte NON, il est à
1. Lorsque le signal d'appel est lui-aussi à 1, alors le signal derrière la
porte ET est à 1, et le moteur est
commandé. |
Table de vérité
Commande logique
Commande =
(Non RdeC) ET
(Appel) |
||||||||||||||||
|
Nous venons de
rencontrer trois opérateurs (connecteurs ou portes) logiques: -
le Non inverse les choses; -
le ET exprime l'un et l'autre; et -
le OU signifie l'un ou l'autre. Leurs
combinaisons permettent d'exprimer toutes les fonctions logiques rencontrées
dans l'ascenseur comme dans de nombreuses autres applications, comme
l'ordinateur. Et aussi pour
raisonner en français de tous les jours … |
|
|
||
|
Mon
premier raisonnement
Or, au pied d'un lampadaire allumé, le chat
roux ne sera pas gris. Il faudrait être plus précis et dire: la nuit, par
faible clair de lune et aucune autre lumière, tous les chats sont gris.
Alors, la nuit, par faible clair de lune et aucune autre lumière, mon chat
est gris. |
||
|
|
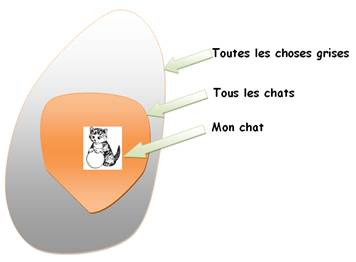
Diagramme montrant
les ensembles et leur imbrication
Tous les chats sont gris la nuit; mon chat est gris la nuit |
|
|
|
||
|
|
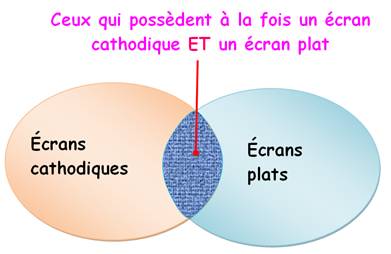
Diagramme
Ceux qui possèdent les deux écrans: Intersection de deux ensembles Ceux qui possèdent un écran: Réunion de deux ensembles Devinette Nous connaissons 100 personnes qui ont des téléviseurs. Parmi elles 70
ont un écran plat et 50 ont un écran cathodique. Combien possèdent les deux? Réponse: 70 + 50 = 120, or ils ne sont que 100. Donc, 20 possèdent à la
fois le cathodique et le plat. |
|
Nous
retenons
|
La logique classique s'applique aussi bien à la
représentation de fonctions logiques à la base de la réalisation de l'électronique numérique et de l'informatique. La logique
s'applique aussi au raisonnement habituel
en français, dit calcul des propositions. L'algèbre booléenne (ou de Boole) est une abstraction
mathématique, outil qui
s'applique à de nombreux domaines dont la théorie des ensembles et la logique propositionnelle. |
|
|
|||
|
L'art de penser On a
appris le calcul, l'orthographe, l'histoire, etc. Mais a-t-on appris à penser
? La
logique est l'art de penser. Discipline ancienne et aussi très moderne car au
cœur de l'informatique. La
logique étudie les conditions d’un raisonnement valide, autrement dit qui
examine si on utilise de manière correcte le mot "donc". La
logique se concentre sur la structure et sur la forme du raisonnement,
indépendamment de son contenu. |
Logique: math ou philo La logique est un domaine des maths ou de la philosophie. On y trouve
des théorèmes et des démonstrations; mais, elle n'utilise pas de chiffres et
ne calcule rien comme le calcul ou l'algèbre. La logique ne doit pas être confondue avec l’argumentation. La
première a pour objectif de prouver, la deuxième celui de convaincre. La
logique se concentre sur la structure et sur la forme du raisonnement,
indépendamment de son contenu. |
||
|
Le biais cognitif Un
raisonnement peut sembler vrai car on sait que la conclusion est vraie. Un raisonnement
peut être déclaré faux car on sait pertinemment que la conclusion est fausse. Un biais
cognitif agit comme une illusion d'optique qui nous fait prendre pour logique
ce qui ne l'est pourtant pas. |
Tous les hommes ont un nez
Même structure dans les deux cas. Les deux lignes de raisonnement sont
toutes deux fausses. |
||
|
Trois étapes
Les critères
d’évaluation sont différents à chaque étape. Un concept est utile ou moins
utile, une proposition est vraie ou fausse, un raisonnement est correct ou
incorrect. |
On conceptualise d’abord quelque chose, On en pense ensuite quelque chose, On en déduit quelque chose, |
||
|
Concept |
Classement des choses selon la perception de chacun,
même s'il existe une grande part partagée. Un paquet de bonbons est considéré comme un objet
tout comme l'est le bonbon lui-même |
||
|
Qualification des concepts |
La chose est ceci ou cela. Le bonbon est acidulé,
sucré, un plaisir pour le palais, mauvais pour la santé … |
||
|
Enchainements |
La pensée doit aligner des jugements pour
produire un raisonnement, pour déduire une ou des conclusions à partir de
prémisses |
||
D'après La
Logique – Phanie – L'Écho – 01/06/2019
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()