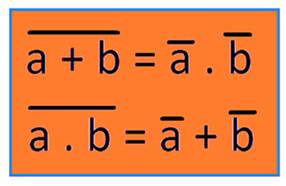loi de la logique, fonction OU exclusif

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/04/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Logique	Rubrique LOGIQUE				Glossaire Logique
	Lois de la LOGIQUE
Inversion		ET	OU	Implication
Phrases			OU Exclusif	Équivalence
		Multi-variable	Addition
Sommaire de cette page >>> Approche avec le "OU EXCLUSIF" >>> Avec trois variables >>> Additionneur >>> Théorèmes de De Morgan >>> Plus de quatre variables

LOGIQUE MULTI-VARIABLE

Diagramme de Karnaugh

Comment simplifier une fonction logique, une fonction booléenne ?

Simplement avec une représentation schématique!

Anglais: Simplification of Boolean Functions

Approche avec le "OU EXCLUSIF"

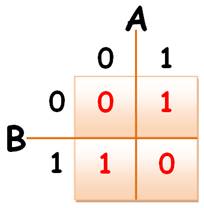
Table de vérité

A	B	S = A B
0	0	0
0	1	1
1	0	1
1	1	0

Voir Ou exclusif

Diagramme de Karnaugh

Voir Diagramme de Karnaugh

Le diagramme de Karnaugh indique qu'elle est la valeur de la fonction S pour toutes les valeurs possibles des variables A et B. La fonction S vaut 1 chaque fois qu'une case vaut 1.

S = 1 si A vaut 1 et B vaut 0 ou bien si A vaut 0 et B vaut 1.

Note: retenons que cette configuration en diagonale correspond au ou exclusif (S vaut 1 si A ou B vaut 1, mais pas les deux à la fois).

En présence de plusieurs variables, il est souvent plus facile d'utiliser le diagramme de Karnaugh que la table de vérité.
Il est plus facile d'y déceler des configurations qui conduisent à une fonction logique simplifiée.

Avec trois variables

Avec trois variables A, B et C, le diagramme se présente comme indiqué ci-contre.

Essayons de formuler la configuration indiquée avec les chiffres en rouge.

La variable de sortie S est à 1 pour toutes les cases qui sont à 1 dans ce diagramme.

On peut citer tous les 1, comme le 1 en haut à droite: A vaut 1 et B vaut 0 et C vaut 0, soit .

Mais, il est plus malin de regrouper:

Comme les deux 1 de la colonne de gauche: A vaut 0 et C vaut 1, B vaut 0 ou 1, il n'a pas d'influence. Bilan, la colonne de gauche donne .

La colonne de droite nous donne:

Au total la fonction S qui représente tous les 1 de ce diagramme est:

En résumé:

S ne dépend pas de B; pour que S soit égal à 1, il suffit que A ou C vaille 1 => fonction OU

Mais, A et C ne doivent pas être à 1 tous les deux => fonction OU exclusif.

On peut encore simplifier en notant:

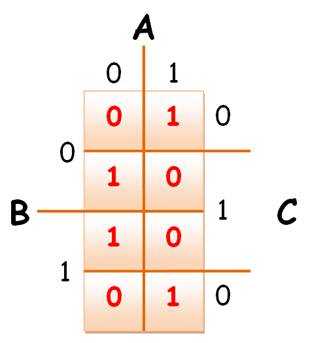
Notations

Si A vaut 1, on note

Si A vaut 0, on note (surligné)

Si A et B sont à 1, on note AB

Si A ou B sont à 1, on note A+B

Diagramme de Karnaugh à trois variables A, B et C

Valeur de S

La fonction S vaut 1 chaque fois qu'une case du diagramme vaut 1.

Avec les trois variables de l'additionneur

La somme de deux bits A et B a été étudié et nous rappelons les diagrammes qui donnent la valeur de la somme S et de la retenue R.

Lorsque des 1 se présentent en diagonale, on est en présence de Ou exclusif. Il est un peu plus coriace ici que ci-dessus. Il s'agite, en fait, de deux ou exclusif emboités.

La retenue va nous amener à débusquer un Ou exclusif, aussi!

D'abord les cellules f et h nous donnent AB.

Restent à coder les deux cellules en diagonales en d et e.
Elles sont dans la zone de C = 1.
Elles sont en diagonales et correspondent à

Bilan

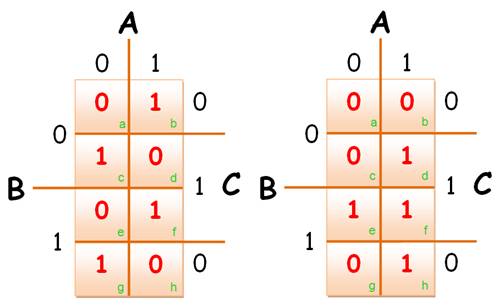
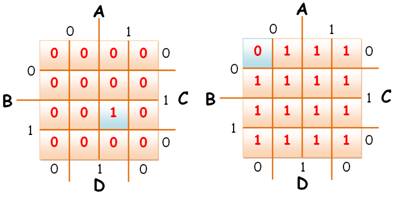
Diagramme pour S et diagramme pour R

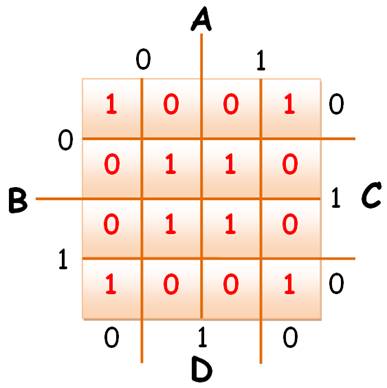
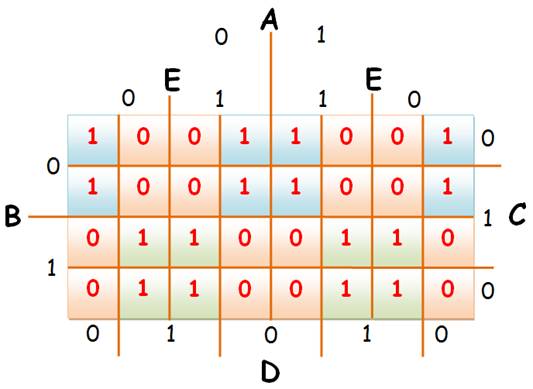
Avec les quatre variables

Voici un diagramme de Karnaugh à quatre variables A, B, C et D.

Quelle est la fonction S pour une telle configuration? Il y a de la diagonale dans l'air!

les quatre 1 du centre correspondent à C = 1 et D = 1;

les quatre 1 des coins correspondent à C = 0 et D = 0.

Nous pouvons chercher à évaluer la fonction qui ne donne que des 0:

Les quatre 0 en haut er en bas sont dus à C = 0 et D = 1;

Les quatre 0 à gauche et à droite sont dus à C = 1 et D = 0;

Avec ces deux évaluations, l'une donnant le complément de l'autre, nous montrons la possibilité de démontrer des relations logiques.

Théorèmes de De Morgan

ou Lois de De Morgan (lois de Morgan*)

Principal intérêt

Passer d'une fonction ET à une fonction OU;

Et, inversement

Le NON d'un OU est identique au ET des NON de chaque variable.

Le NON d'un ET est identique au OU des NNON de chaque variable.

La barre de surlignement symbole la fonction NON.

Théorème de De Morgan

Les deux célèbres théorèmes de De Morgan se déduisent facilement à partir d'un diagramme de Karnaugh.

Diagramme de gauche:

S vaut 1 si les quatre variables sont à 1.

S vaut 0 dès que l'une des quatre variables est à 0.

Diagramme de droite:

S vaut 1 si l'une des quatre variables est à 1.

S vaut 0 si les quatre variables sont à 0.

On résume parfois en disant que le complémentaire d'une fonction est obtenu en prenant le complémentaire de chaque terme et en inversant les opérateurs.

Loi de Morgan avec deux propositions P et Q:

Exemples

P: il est grand;

Q: il a 15 ans ou plus.

Pas vrai que (il est chauve et il a 65 ans ou plus).

devient:

(il n'est pas chauve) ou (il n'a pas 65 ans ou plus).

(il est chevelu) ou (il a moins de 65 ans).

Phi n'est pas inférieur à et n'est pas non plus supérieur à 2.

Pas vrai que (Phi <1) et que (Phi < 2)

devient:

(Phi 1 ou Phi 2), ce qui est vrai.

* Par souci d'euphonie; Augustus De Morgan (1806-1871) >>>

Voir Théorème de De Morgan concernant la coloration des graphes

Plus de quatre variables

On continue à tourner autour du cadre. Avec 5 variables, la nouvelle variable E partage le haut du cadre avec A. Attention à l'ordre des valeurs 0 et 1 pour E.

Dans la configuration présentée, exprimons S:

pour les cases vertes