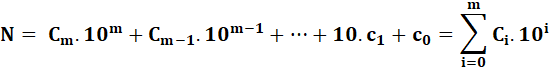|
|||||||||||||||||||||||||||||||||||
![]()
|
COMPTER – Approche du système décimal
Principe
de la numération à base 10, notre manière classique de compter. |
Ce que disait Aristote (de -384 à -322)
|
Aristote
prolonge son propos en énumérant la manière de représenter sur les doigts tous les nombres de 1 à 9
000. Aristote –
Problèmes, XV 910-911 |
Extrait
de Compter avec des cailloux – Alain Schärlig / Cité
aussi par Tangente n°177
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Symboles et positions
Ce que cela veut dire
Exemple: 253
"décortiqué"
|
|||||||||||||||||||||||||||||||||||||||||||||
Si vous voulez débuter plus en douceur >>>
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple de représentation: 4 307
Formulation générique N Un nombre. C Un chiffre de 0 à 9. m La quantité de chiffres du nombre.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemple: 0,4307
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Decimal Day
|
Le
15 février 1971 est le décimal day (jour décimal)
pour les Britanniques. leur monnaie devient décimale: une livre est divisé en
100 pence. L'ancien système
divisait la livre en 20 shillings et le shilling en 12 pence (240 pence par
livre). Note: un penny, des pence. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Numerati/ConDecim.htm
|
![]()
Renvoi de lien
Conversion d’un Nombre Périodique en fraction >>>