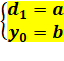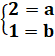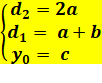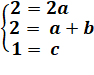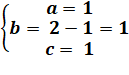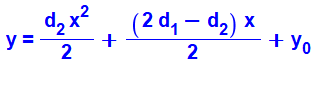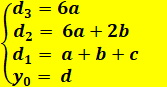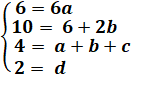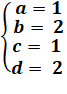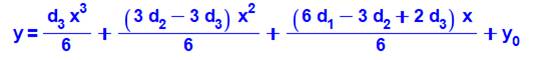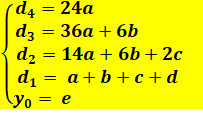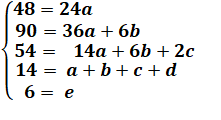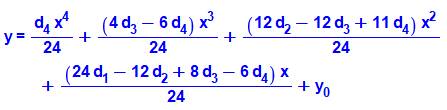Accueil

Orientation générale

Barre de recherche

DicoNombre

DicoMot Math

DicoCulture

Atlas des maths

Rubriques

Index alphabétique

Nouveautés

Actualités

Références

Édition du: 29/01/2022

M'écrire

Brèves de Maths

 

INDEX

 

Suites

Combinatoire

Sommes de nombres

SUITES NUMÉRIQUES

Méthode des différences

Calculs sur les suites

Polynômes représentatifs

Coefficients binomiaux

Fractions

Faites un double-clic pour un retour en haut de page

 

 

 

SUITES – Méthode des différences

Polynômes représentatifs

 

Application de la méthode des différences

*      Calcul des différences successives jusqu'à obtenir une valeur constante;

*      Identification des nombres de tête des différences;

*      Appairage de ces nombres aux premiers nombres de la suite;

*      Résolution des équations (simples); et

*      Définition du polynôme représentatif de la suite.

     

 

Sommaire de cette page

>>> Premier degré 

>>> Deuxième degré 

>>> Troisième degré 

>>> Quatrième degré 

 

Débutants

Dénombrement

 

Glossaire

Compter


Voir Bases de la méthode des différences

 

Calcul des différences – Premier degré

haut

 

 

Fonction du premier degré

y = ax + b

 

 

 

 

Équations d'après le tableau

 

 

Calcul des différences
x est l'indice du rang de la valeur;
y la valeur de la série pour cet indice; et
d1 est la première différence entre deux termes successifs de la série.
Ex: (a + b) – (b) = a; (2a + b) – (a + b) = a; …

 

Tableau: x, y et d1

 

x

0

1

2

3

…

y

b

a + b

2a + b

3a + b

…

d1

a

a

a

a

 

 

 

Exemple

 

La suite choisie est: 1, 3, 5, 7, … qui est la suite des nombres impairs.

 

La fonction trouvée est naturellement: y = 2x + 1.

 

 

Valeurs de y et calcul de d1

 

x

0

1

2

3

y

1

3

5

7

d1

2

2

2

  

 

Recherche de l'équation pour cette série

 

 

y = 2x + 1

 

 

Sous forme de polynôme avec les différences

            y = ax + b     =      d1 · x + y0

 

 

 

Calcul des différences – Deuxième degré

haut

 

Fonction du deuxième degré

 

y = ax² + bx + c

 

Équations

 



 

 

Calcul des différences
d2 est la deuxième différence: écart entre deux valeurs successives de la première différence. Ex: d22 = (3a + b) – (a + b) = 2a

 

x

0

1

2

3

…

y

c

a + b + c

4a + 2b + c

9a + 3b + c

…

d1

a + b

3a + b

5a + b

 

d2

 

2a

2a

2a

 

 

Exemple

 

La suite choisie est:
1, 3, 7, 13, 21, 31, …

 

La deuxième différence est constante, la fonction est du deuxième degré.

 

Valeurs de y et calcul de d1 et de d2

 

x

0

1

2

3

4

5

y

1

3

7

13

21

31

d1

2

4

6

8

10

d2

 

2

2

2

2

 

 

Recherche de l'équation pour cette série

 

 

 

y = x² + x + 1

 

 

Sous forme de polynôme avec les différences

En remplaçant a, b et c par leur valeur.

 


Cas d'une série dont le premier rang est 1

 

Polynôme pour cette série ?

 

x

1

2

3

4

5

6

y

0

2

6

12

20

30

d1

2

4

6

8

10

d2

 

2

2

2

2

 

Choisir les bonnes colonnes !

 

d22 = 2 = 2a  => a = 1

 

d12 = 2 = 3a + b = 3 + b =>  b = – 1  

 

y1 = 0 = a + b + c = 1 – 1 + c => c = 0

 

y = x² – x  = x (x – 1)

y = 0×1 + 1×2 + 2×3 + 3×4 + …

 

 

 

 

Calcul des différences – Troisième degré

haut

 

Fonction du troisième degré

 

y = ax3 + bx2 + cx + d

 

Équations

 



 

 

Calcul des différences

 

x

0

1

2

3

…

y

d

a+b+c+d

8a+4b+2c+d

27a+9b+3c+d

…

d1

a + b + c

7a + 3b + c

19a + 5b + c

 

d2

 

6a + 2b

12a + 2b

 

d3

 

 

6a

 

 

 

Exemple

 

 

La suite est celle indiquée sur la ligne y.

 

x

0

1

2

3

4

5

y

2

6

20

50

102

182

d1

4

14

30

52

80

d2

 

10

16

22

28

d3

 

 

6

6

6

 

 



y = x3 + 2x2 + x + 2

 

Sous forme de polynôme avec les différences

En remplaçant a, b, c et d par leur valeur.

 

 

 

 

Calcul des différences – Quatrième degré

haut

 

Fonction du quatrième degré

 

y = ax4 + bx3 + cx2
          + dx + e

 

Équations

 



 

 

Calcul des différences

 

x

0

1

2

3

4

…

y

e

a+b+c+d+e

16a+8b+

4c+2d+e

81a+27b+

9c+3d+e

256a+64a+

16c+4d+e

…

d1

a+b+c+d

15a+7b+

3c+d

65a+19b+

5c+d

175a+37b+

7c+d

 

d2

 

14a+6b

+2c

50a+12b

+2c

110a+18b

+2c

 

d3

 

 

36a+6b

60a+6b

 

d4

 

 

 

24a

 

 

 Remarquez que 24  = 4! comme 4 de la différence quatrième.

  

 

Exemple

 

 

La suite est sur la ligne y.

 

x

0

1

2

3

4

5

y

6

20

88

300

794

1756

d1

14

68

212

494

962

d2

 

54

144

282

468

d3

 

 

90

138

186

d4

 

 

 

48

48


y = 2x4 + 3x3 + 4x2 + 5x + 6

 



a = 2

90 = 72 + 6b

6b = 18 => b = 3

54 = 28 +18 + 2c

c = (54 – 46)/2 = 4

14 = 2 + 3 + 4 + d

d =5

 

 

 

Sous forme de polynôme

En remplaçant a, b, d et e par leur valeur

 

 

 

 

 

Haut de page

 

Retour

*      Calculs sur les suites

Suite

*      Suites et coefficients binomiaux

Voir

*      Liens pour ces pages

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Suite/aSuite/SuiDif02.htm