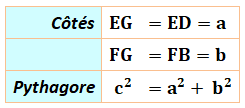|
Édition du: 28/10/2023 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
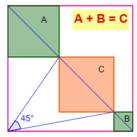
Trois
carrés le long de la diagonale d'un grand carré, celui du milieu étant
intercepté par un angle de 45°. La somme des aires des deux carrés d'extrémité
est égale à l'aire du carré central. Ce défi géométrique est classé dans liste des défis
complexes. C'est avoir l'idée des constructions complémentaires qui n'est pas
évident; ensuite, la résolution est assez simple. |
||
|
|
Sommaire de cette page >>> Trois carrés plus un |
Débutants Glossaire |
|
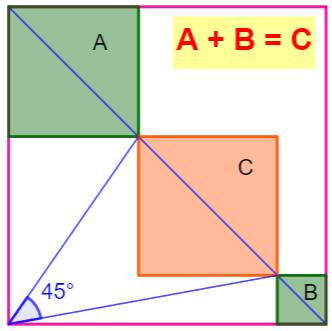
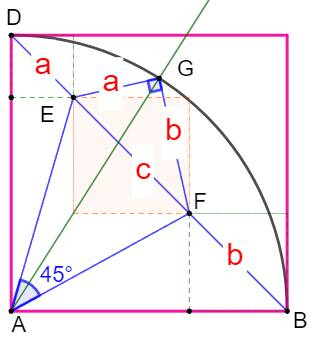
Construction Un grand carré
et l'une de ses diagonales. Un angle de
45° intercepte une portion de cette diagonale (voir figure). Sur chacun des segments découpés sur la
diagonale, on dessine un carré. Montrer que la somme des aires des carrés verts
(A + B) vaut l'aire du carré orange (C). Piste (pas
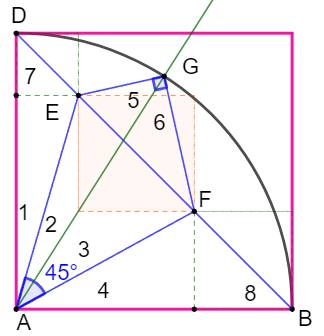
simple à trouver !) La figure possède des propriétés cachées qui seront
révélées en traçant:
Alors, le point G s'avérera être le sommet d'un
angle droit. Application du théorème
de Pythagore dans le triangle
rectangle GEF. |
|
|
|
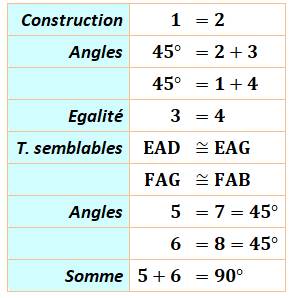
Analyse des angles
Voir Triangles
semblables |
|
|
|
Comparaison des longueurs
Conclusion Les carrés de côté DE et FB totalisent une aire
égale à l'aire du carré de côté EF. C'est une variante de ce que l'on cherche. Ces portions de diagonale sont, en fait, les diagonales
des carrés à considérer. Or, diagonales et carrés sont dans la proportion √2. Donc l'égalité tient aussi pour les carrés d'origine.
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/CarreTro.htm
|