|
Édition du: 30/01/2025 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
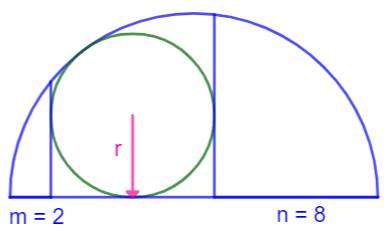
Figures dans le demi-cercle Rayon ? Un cercle est
inscrit dans un demi-cercle, limité par deux perpendiculaires au diamètre du
demi-cercle. Quel est son rayon ? Un demi-cercle
et deux perpendiculaires. Trouver l valeur du rayon. |
||
|
|
Sommaire de cette page >>> Le cercle dans le demi-cercle >>> Le trapèze dans le demi-cercle |
Débutants Glossaire |
|
Construction Un demi-cercle de rayon R inconnu. Un cercle vert compris entre deux
perpendiculaires au diamètre et situées aux cotes 2 et 8 à partir de chaque extrémité
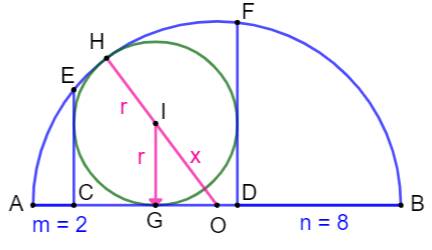
du diamètre. Quelle est la valeur du rayon r du cercle ? Piste On trace le rayon R. Alors, il existe plusieurs façons d'évaluer sa
longueur en fonction de r.
Avec ces trois équations, on est en mesure de
connaitre les trois inconnues r, R et x. On remarque que le triangle OGI est rectangle et
donc passible du théorème
de Pythagore. |
|
|
|
Calculs
|
||
|
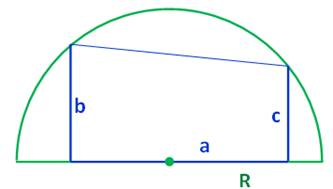
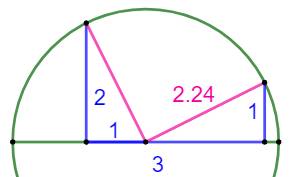
Construction Un demi-cercle de rayon R inconnu. Deux segments perpendiculaires au diamètre, de
longueur b et c, espacés d'une distance a. La figue forme un trapèze
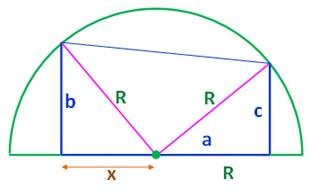
rectangle. Quel est le rayon du demi-cercle ? Application: a = 3; b = 2 et c = 1. Piste (Figure
du bas) On trace les rayons roses. De sorte que l'on
forme deux triangles rectangles. Le théorème
de Pythagore entre en action et le tour est joué ! Calculs
|
Figure initiale
Notations
Vérification
|
|
|
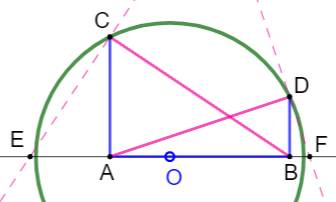
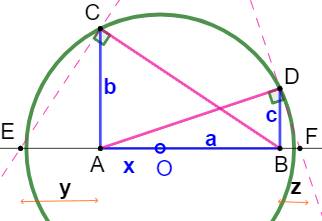
Construction Les points A, B, C et D sont connus. Il faut construire le demi-cercle passant par C
et D et tel que AB porte le diamètre. 1)
Perpendiculaires CE à BC et DF à AD; 2)
Intersection avec la droite AB en E et F; 3)
Point O milieu de EF; 4)
Cercle de centre O et de rayon OC, ce cercle passe également par D. Justification (Figure
du bas)
|
|
|
Voir Relations
métriques dans le triangle rectangle
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/CerDemi.htm
|