|
Édition du: 13/10/2023 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Deux cercles dans un rectangle Deux
cercles tangents et tangents aux côtés d'un rectangle. Trouver la longueur du
rectangle. Trois
autres défis géométriques avec deux cercles dans
un rectangle |
||
|
|
Sommaire de cette page >>> Longueur du segment vert >>> Rayon du petit cercle >>> Longueur du segment vert >>> Avec la diagonale |
Débutants Glossaire |
|
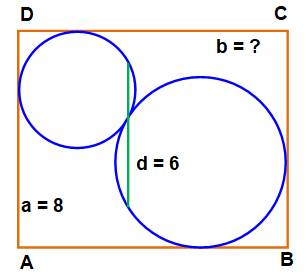
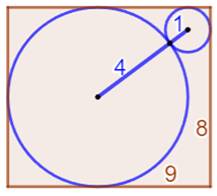
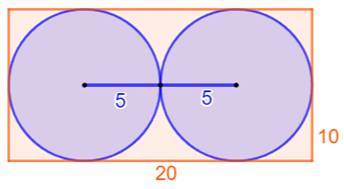
Construction Un rectangle
ABCD et deux cercles intérieurs tangents
et chacun tangent aux côtés du rectangle. Le trait vert passant par le point de tangence et
parallèle au côté AD mesure d = 6. Trouver la mesure du côté AB = CD = b. Piste 1 EG est une corde perpendiculaire au rayon porté
par OP, et par symétrie,
EH = HG. De même GH' = H'F Au bilan: HH' = ½ EF = 6/2 = 3 = OM =
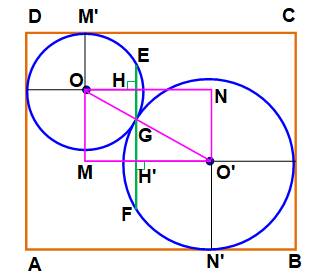
NO'. Piste 2 On réalise les tracés de la figure du bas, et
cela à partir du rectangle ayant pour sommets les centres des cercles. Alors:
MO'+ 5 = b Avec le théorème
de Pythagore dans le triangle rectangle OMO': MO'² = OO' – OM² = 5² – 3 ²
= 4² Bilan b = MO' + 5 = 4 + 5 = 9 |
Figure de l'énoncé
Figure pour la solution
|
|
D'après Answer
To Ancient Trick To Solve This Puzzle – Mind Your Decision – Presh
Talwalkar
|
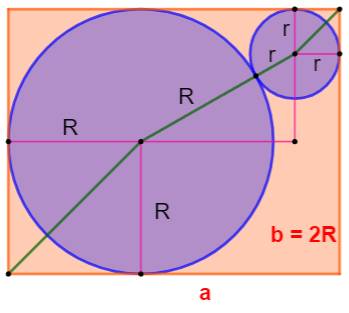
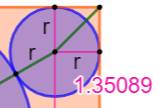
Construction Un rectangle orange de longueur a = 10 cm et de
largeur b = 8 cm. Un cercle tangent à trois côtés du rectangle. Quelle est le rayon maximum du cercle logeable
dans l'espace orange restant ? Pistes Sur la figure, on note les segments de longueur R
et ceux de longueur r. On remarque que le grand cercle bleu a un rayon R
égal à la moitié de la largeur b du rectangle. On évalue la largeur b du rectangle en fonction
de R et r. Le théorème
de Pythagore permet l'évaluation du segment central. |
|
||
|
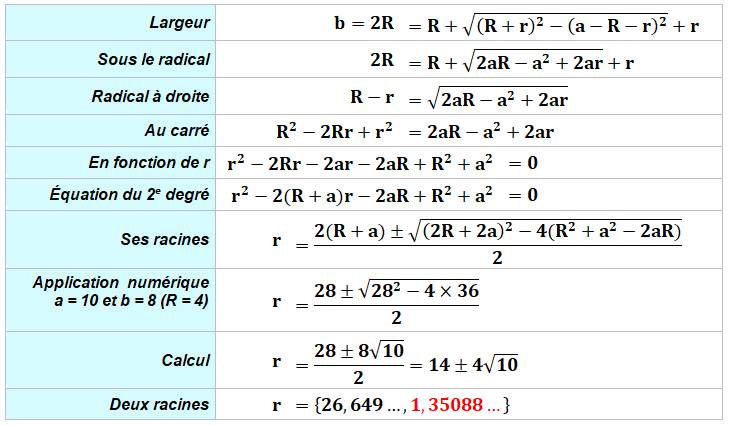
Calculs
|
|||
|
Vraisemblance En traçant la figure à l'échelle, on constate que
seule la valeur r = 1,35088… est recevable. L'autre valeur est un artefact dû
à l'élévation au carré. |
|
||
|
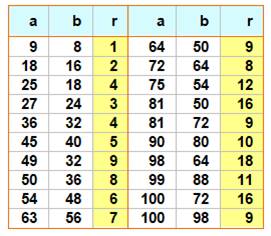
Valeur entières pour r Quelles sont les valeurs de a et b telles que r
soit un nombre
entier. Le tableau recense les vingt cas pour a et b
jusqu'à 100. On sait que pour a = 2b, les deux cercles sont
égaux (rayon égal à b/2). Ces cas ne sont pas répertoriés dans le tableau. Notez que le second cercle n'existe à l'intérieur
du rectangle que si a < 2b Le cas a = b correspond au cas où le rectangle devient
un carré; alors, le second cercle a un rayon nul. |
|
|
Exemple avec a = 2b
|
|
|
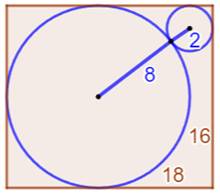
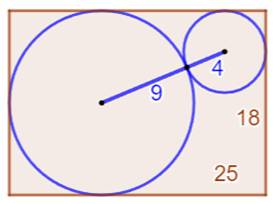
Construction Figure du type précédent avec valeurs entières des
côtés du rectangle: Tangente
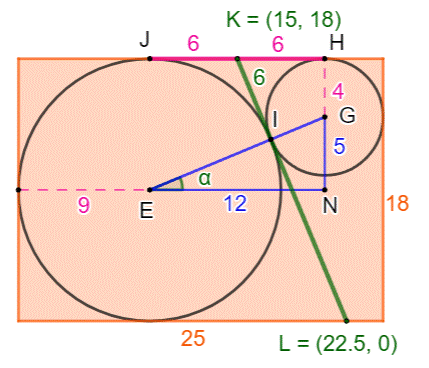
verte aux deux cercles qui coupent le rectangle en K et L. Quelle est la longueur du segment vert ? Pistes On connait le rayon des cercles: R = 9 et r = 4 (exercice précédent). Les segments
de tangentes à partir du point K sont égaux. Ils mesurent: Coordonnées du point K = (15, 18). Reste à connaitre celles du point L. On va passer
par l'équation
de la droite EG. Puis à celle qui lui est orthogonale
KL. |
|
|
|
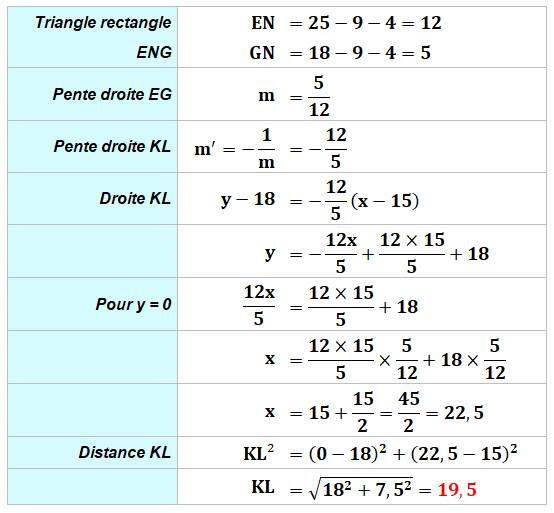
Calculs
|
||
|
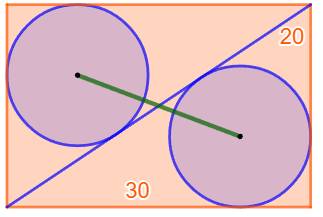
Construction Un rectangle de dimensions 30, 20. Deux cercles tangents à deux côtés du rectangle
et à la diagonale. Quelle est la longueur du segment vert joignant
les deux centres des cercles ? |
|
|
|
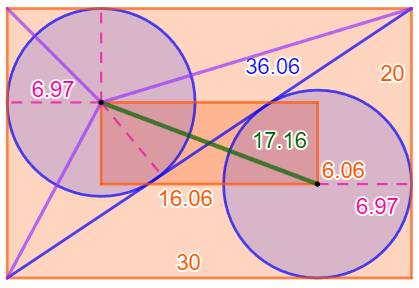
Pistes Dans un premier temps, il est judicieux de
connaitre le rayon R des cercles. L'astuce consiste à évaluer l'aire de l'un
des triangles rectangles de deux manières différentes. On connait l'aire du demi-rectangle. Cette aire
est aussi la somme des aires de trois triangles (traits violets) dont la
hauteur commune est R. Il est assez simple, alors de connaitre les
dimensions du rectangle interne (orange) et de sa diagonale. |
|
|
|
Calculs
|
||
Sur une idée de Mind Your Decision – Presh Talwalkar: Distance
Between Two Inscribed Circles In A Rectangle
![]()
|
Retour |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/RectCerl.htm
|