|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
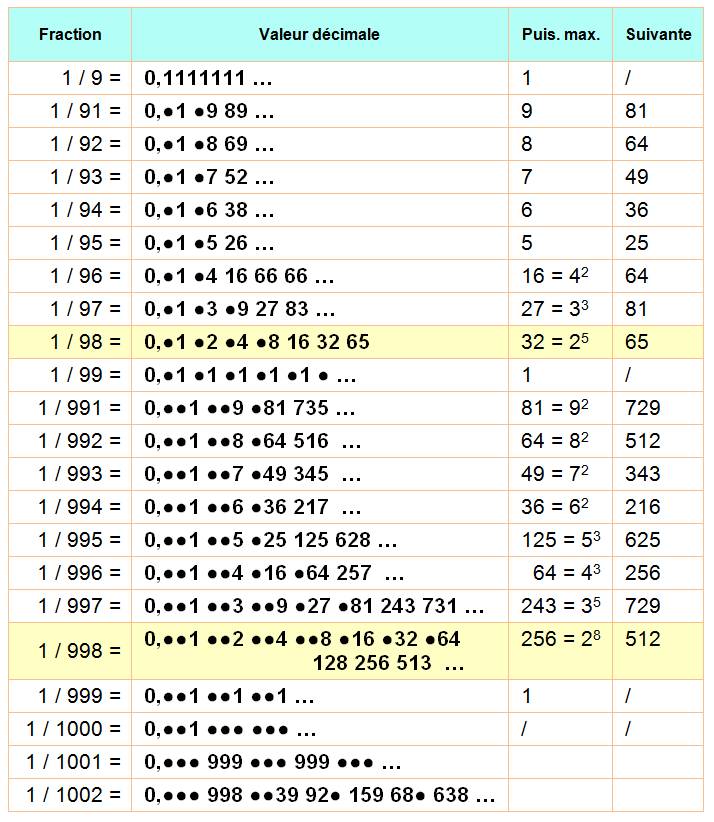
FRACTIONS engendrant des PUISSANCES Fractions en 1/ (10k – n) Magie des nombres et des fractions.
Certaines fractions contiennent en elles-mêmes toutes les puissances
énièmes des nombres successifs, les multiples et même la
suite de Fibonacci. Exemple avec les puissances de 2
|
Voir Nombre
périodiques / Développement
décimaux remarquables
|
|
|
|
Les 0 derrière la virgule sont remplacés par des points
pour mieux apprécier la structure.
Remarque Avec 1/ 1002, le 0998 soustrait de 1002 (fraction en 1
/998) donne 4, puis, en poursuivant, on obtient les puissances de 4. En effet 1/998 – 1/1002 = 1/24999 = 0,000004
000016 000064 000256 … |
|
|
|
||
|
Principe de la construction par addition
C'est la somme des fractions
suivantes:
|
||
|
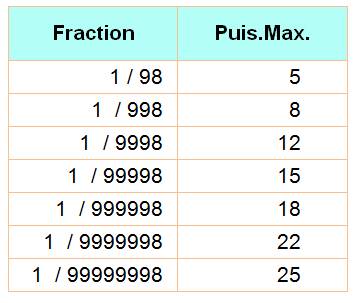
Jusqu'à quelle puissance?
|
|
|
|
|
||
La 16e
fraction avec les puissances de 2
sur trois chiffres
![]()
|
Principe de la construction par division
|
|
|
Cas de la fraction 1/49
|
1 / 98 = 0,1020408163265… 1 / 49 = 0, 20408163265… 1 / 24,5 = 0.
408163265 |
|
|
||
|
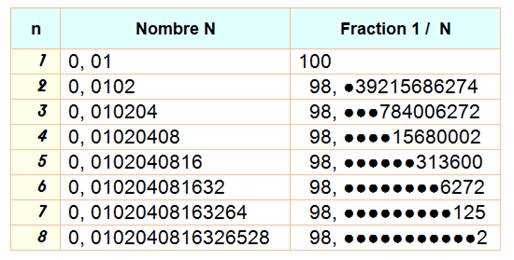
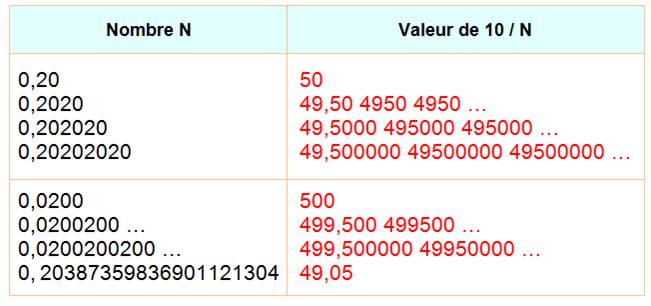
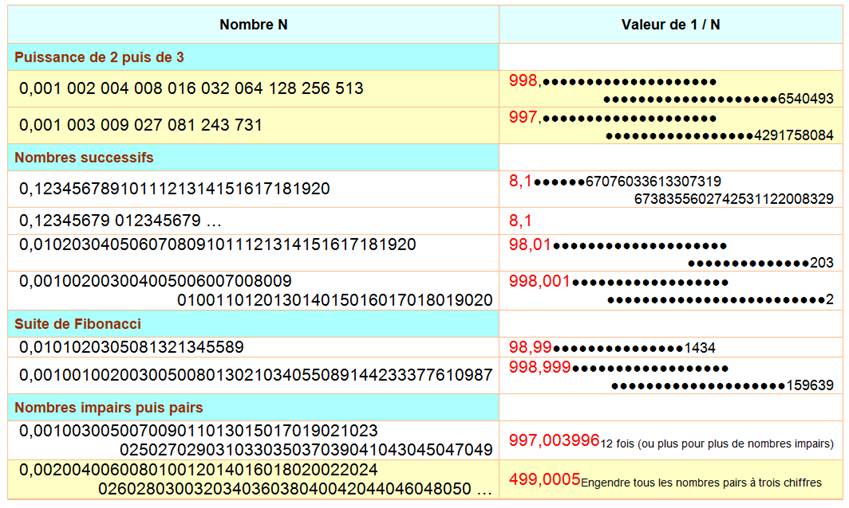
Présentation du tableau
La calculette de votre
ordinateur vous donnera 32 chiffres. Voir Ci-contre.
C'est le cas pour 0,001002003 … = 1 /
998
C'est le cas des nombres successifs sans 0 intercalaires. Comme: 1 / 8,100000067076….
C'est le cas de la suite des nombres pairs avec 1 / 499,0005. |
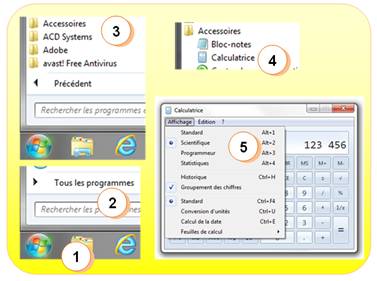
Utilisation de la calculatrice de
l'ordinateur
1) Cliquez sur l'icône Windows 2) Sur tous les programmes 3) Sur Accessoires 4) Sur calculatrice 5) Ouvrir Affichage et cochez scientifique |
|
Voir Calculatrice
Quelques
valeurs typiques – Table
|
|
||
|
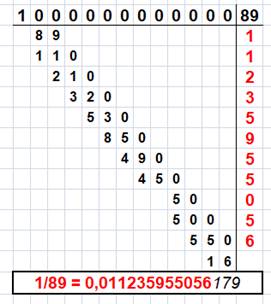
Rappel de la suite de Fibonacci 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 … Notez
que F11
= 89 Nombre 89 Le
développement décimal de la fraction 1/89 fait apparaitre les
premières valeurs des nombres
de Fibonacci: 1, 1, 2, 3, 5 (Division
longue ci-contre). Notez
les restes: on y retrouve les deux nombres à sommer: (1+1), (2+1),
(3+2), … La
suite cache elle aussi les nombres de Fibonacci suivants? En
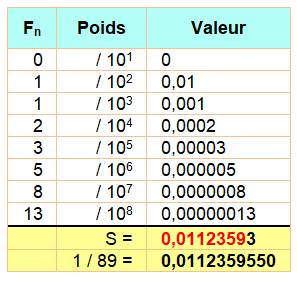
effet, la somme des nombres de Fibonacci pondérée par les
inverses des puissances de 10 reconstruit progressivement la valeur de la
fraction 1/89 en tenant compte des retenues(Tableau). Notez que le dénominateur 89 est
lui-même un nombre de Fibonacci (coïncidence). |
Une simple division montre déjà un
résultat 1 / 0,0112358 = 89,0012… En reprenant à l'envers 1 / 89
Somme pondérée des nombres de Fibonacci
|
|
Suite en Pourquoi
1/89 et polynômes générateurs /
Somme complète des Fibonacci
= 1/ 89 (page Excel)
|
|
|
|
|
|
|
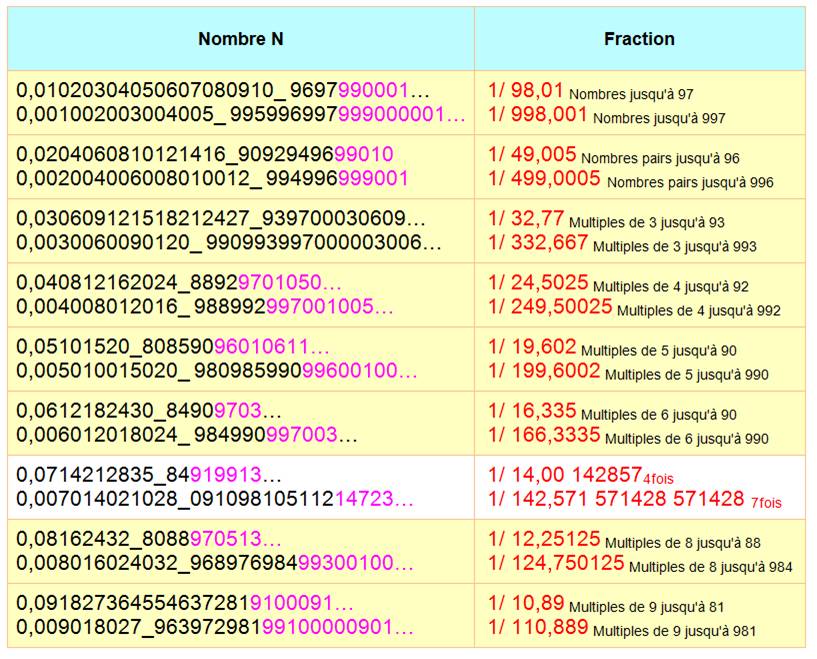
998,
997, 996 … produisent les puissances successives de 2, 3, 4 … 999,001 produit
la succession des nombres entiers 499,005
produit celle des nombres pairs |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()